Универсальное уравнение состояния идеального газа
Уравнению Клапейрона можно придать универсальную форму, если газовую постоянную отнести не к 1 кг газа, а к 1 кмоль.
Итальянский ученый Авогадро в 1811 г. доказал, что при одинаковых температурах и давлениях в равных объемах различных идеальных газов содержится одинаковое количество молекул. Из закона Авогадро вытекает, что плотности газов, находящихся при одинаковых температурах и давлениях, прямо пропорциональны их молекулярным массам: 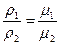
где μ1 , μ2 — молекулярные массы газов.
Молекулярной массой таза называется численное выражение отношения массы молекулы данного вещества к 1/12 массы атома изотопа углерода 12С.
Количество вещества, содержащее столько же молекул (атомов частиц) сколько атомов содержится в нуклиде углерода 12С массой 12 кг (точно) называется килограмм-молекулой или киломолем, газа (кмоль).
Отношение плотностей газов в уравнении (а) можно заменить обратным отношением удельных объемов.
тогда  откуда V1μ1 = V2μ2
откуда V1μ1 = V2μ2
Это соотношение показывает, что при одинаковых физических условиях произведение удельного объема газа на его молекулярную массу есть величина постоянная и не зависит от природы газа:
Vμ = const
Произведение Vμ есть объем 1 кмоль идеального газа, а уравнение показывает, что объемы киломолей всех газов при равных температурах и давлениях одинаковы.
Напишем уравнение состояния для. 1 кмоль газа: PVμ = μRT
Откуда 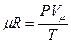
Произведение μR называют универсальной газовой постоянной.
Универсальная газовая постоянная μR есть работа 1 кмоль идеального газа в процессе при постоянном давлении и при изменении температуры на 10.
При так называемых нормальных физических условиях (давлении 101325 н/м2 и температуре 273,15 0 К) объем 1 кмоль газа равен 22,4143 м3/кмоль, а универсальная газовая постоянная оказывается равной

Универсальное уравнение состояния, отнесенное к 1 кмоль газа, имеет следующий вид:
PVμ = 8314,20 Т.
Это уравнение называют уравнением состояния Клапейрона — Менделеева, так как оно впервые было предложено Д. И. Менделеевым в 1874 г. Уравнение Клапейрона — Мендеелеева является наиболее общим для идеальных газов, так как связывает три закона идеальных газов (Гей-Люссака, Бойля—Мариотта и Авогадро) и включает универсальную газовую постоянную, не зависящую от природы газа.
Зная универсальную газовую постоянную μR, можно подсчитать известную уже нам величину R:
R= 8314,2/ μ дж/(кг-град).
Физические постоянные некоторых газов приведены в табл. 2.
| Газ | Химическая формула | Масса 1 кмоль, кг/кмоль | Газовая постоянная R, дж/кг град) | Плотность газа при Нормальных физических условиях, кг/м3 |
| Кислород | о2 | 259,8 | 1,429 | |
| Водород | н2 | 2,016 | 4124,3 | 0,090 |
| Азот | N2 | 28,02 | 296,8 | 1,250 |
| Окись углерода | СО | 296,8 | 1,250 | |
| Воздух | — | 28,96 | 287,0 | 1,293 |
| Углекислый газ | со2 | 189,9 | 1,977 | |
| Водяной пар | н2о | 18,016 | 461,6 | 0,804 |
| Гелий | Не | 4,003 | 2077,2 | 0,178 |
| Аргон | Аг | 39,944 | 208,2 | 1,784 |
| Аммиак | NH3 | 17,031 | 488,2 | 0,771 |
Выведем основной закон идеальных газов по другому.
Из уравнений [5] и [8] следует, что
р = пkТ.
Рассмотрим 1 кг газа. Произведение концентрации молекул п, т. е. числа молекул в единице объема, и объема одного моля газа Vмоля равно числу молекул в одном моле, т. е. числу Авогадро N А.. NA = пVмоля .
Вместо двух постоянных: универсальной газовой постоянной R и числа Авогадро NA - была введена постоянная k равная отношению 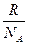 Она получила название постоянной Больцмана k =
Она получила название постоянной Больцмана k = 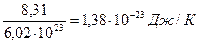 Учитывая, что в нем содержится N молекул и, следовательно, п = N/V, получим: PV/Т=Nk = соnst.
Учитывая, что в нем содержится N молекул и, следовательно, п = N/V, получим: PV/Т=Nk = соnst.
Постоянную величину Nk, отнесенную к 1 кг газа, обозначают буквой R и называют газовой постоянной. Поэтому
рV/Т=R, или PV = RТ. [11]
Полученное соотношение представляет собой уравнение Клапейрона (1834г.).
Умножив [11] на m, получим уравнение состояния для произвольной массы газа m:
PV = mRT [12]
Используя вес G = mg где g =9.8 м/с2 PV = GRT [13]
Уравнению Клапейрона можно придать универсальную форму, если отнести газовую постоянную к 1 кмолю газа, т. е. к количеству газа, масса которого в килограммах численно равна молекулярной массе μ.
Положив в (1.10) М = μ, и V = Vμ, получим для одного моля уравнение Клапейрона — Менделеева
PVμ = μRT [14]
Здесь Vμ — объем киломоля газа, а μR— универсальная газовая постоянная - работа, совершаемая 1 кг газа при нагревании его на 1 0С при Р = const.
В соответствии с законом Авогадро (1811г.) объем 1 кмоля, одинаковый в одних и тех же условиях для всех идеальных газов, при нормальных физических условиях равен 22,4136 м3, поэтому
μR =PVμ/T =101,325 . 22,4136/273,15 = 8314 Дж/(кмоль.К). [15]
Газовая постоянная 1 кг газа составляет R = 8314/μ ; (1.12)
Плотность идеального газа может быть рассчитана с некоторой степенью точности на основе уравнения состояния идеальных газов
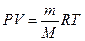 где М – масса 1 кмоль (мольной массы) газа в кг/кмоль
где М – масса 1 кмоль (мольной массы) газа в кг/кмоль
Из уравнения следует 
Объем занимаемый единицей массы газа или удельный объем можно определить по уравнению
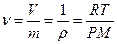
Дата добавления: 2014-12-24; просмотров: 1411;
