Диаграмма направленности линейных и плоских коммутационных решеток
В антеннах с непрерывными фазовращателями фазирование излучающих элементов осуществляется таким образом, чтобы поля от вcex излучателей в дальней зоне в заданном направлении складывались синфазно. Для решеток, изображенных на рис. 3.5, 3.6, требуемое фазовое распределение имеет вид:
линейная решетка излучателей
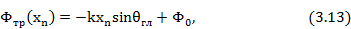
плоская решётка излучателей
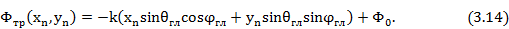
Здесь 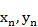 — координаты n-го излучателя в решетке;
— координаты n-го излучателя в решетке; 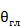 ,
, 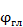 —углы, определяющие направление максимума диаграммы направленности в пространстве;
—углы, определяющие направление максимума диаграммы направленности в пространстве; 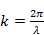 – волновое число;
– волновое число; 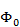 —постоянный фазовый сдвиг, величина которого зависит от выбора начала отсчета фазы.
—постоянный фазовый сдвиг, величина которого зависит от выбора начала отсчета фазы.
В коммутационных решетках в силу дискретного характера изменения фазы токов в излучающих элементах требуемое фазовое распределение не может быть реализовано точно, вследствие чего возникают специфические фазовые ошибки, которые в дальнейшем будут называться коммутационными.
Фазовое распределение, реализуемое в коммутационной решетке, определяемся следующим выражением:
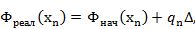
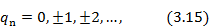
в котором 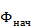 — так называемое начальное фазовое распределение в решетке, которое имеет место в том случае, когда все коммутационные фазовращатели находятся в одной и той же позиции; Δ — дискрет изменения фазы, обеспечиваемый коммутационным фазовращателем;
— так называемое начальное фазовое распределение в решетке, которое имеет место в том случае, когда все коммутационные фазовращатели находятся в одной и той же позиции; Δ — дискрет изменения фазы, обеспечиваемый коммутационным фазовращателем; 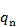 — число последовательных переключений коммутационного фазовращателя от исходной позиции с дискретом изменения фазы Δ.
— число последовательных переключений коммутационного фазовращателя от исходной позиции с дискретом изменения фазы Δ.
В качестве начального фазового распределения 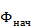 может быть выбрано фазовое распределение на выходе распределительного устройства. Например, в линейных решетках с последовательным распределением энергии путем подключения излучателей с фазовращателями к питающему фидеру с бегущей волной за начальное фазовое распределение может быть принято распределение фаз и в питающем фидере:
может быть выбрано фазовое распределение на выходе распределительного устройства. Например, в линейных решетках с последовательным распределением энергии путем подключения излучателей с фазовращателями к питающему фидеру с бегущей волной за начальное фазовое распределение может быть принято распределение фаз и в питающем фидере:
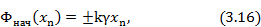
где 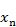 — продольная координата;
— продольная координата; 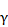 — замедление фазовой скорости в питающем фидере, а выбор знака определяется направлением движения волны в фидере.
— замедление фазовой скорости в питающем фидере, а выбор знака определяется направлением движения волны в фидере.
В плоских решетках начальное фазовое распределение может быть линейной функцией двух координат
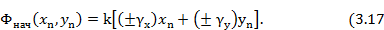 )
)
В схемах квазиоптического типа (см. рис. 3.4) за начальное фазовое распределение может быть принято распределение фаз волны, излучаемой облучателем, на обращенной к облучателю поверхности управляемой линзы. В частности, если плоская управляемая линза находится в раскрыве секториального или пирамидального рупора, т. е. если на внутреннюю сторону линзы падает цилиндрическая или сферическая волна, начальное фазовое распределение имеет вид
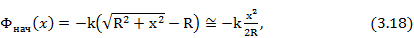
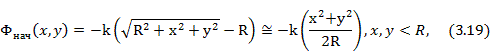
где R длина рупора.
Коммутационные фазовые ошибки определяются следующим выражением:

Дискретный характер работы фазовращателей приводит к увеличению уровня бокового излучения и к скачкообразному движению луча. Фазирование коммутационной антенной решетки может осуществляться различными способами в зависимости от требуемой точности установки луча или уровня бокового излучения в заданном секторе углов. Одним из распространенных способов является фазирование по наименьшей фазовой ошибке, когда для любого излучателя в решетке выполняется условие

В дальнейшем будут рассматриваться коммутационные решетки, фазирование которых осуществляется указанным способом. Максимальная величина коммутационных фазовых ошибок не превышает в данном случае половины дискрета изменения фазы, обеспечиваемого фазовращателем, т. е. 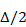 .
.
При фазировании коммутационной решетки в заданном направлении необходимо определить число последовательных переключений каждого фазовращателя от исходной позиции. Эта величина согласно (3.21) определяется следующим неравенством:
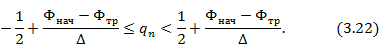
В реальных коммутационных решетках это неравенство решается электронным вычислителем и результат передается в устройство, управляющее фазовращателями.
В случае линейной решетки с начальным распределением фаз (3.16) функция распределения коммутационных фазовых ошибок 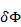 и реализуемое распределение фаз в решетке
и реализуемое распределение фаз в решетке 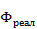 имеют вид
имеют вид
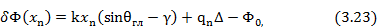
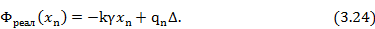
При этом величина 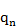 определяется неравенством
определяется неравенством
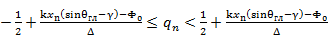 . (3.25)
. (3.25)
Формулы (3.23) — (3.25) соответствуют движению волны в питающем фидере в положительном направлении оси X. Указанные формулы справедливы также для плоских решеток, когда начальное фазовое распределение является функцией одной координаты, а луч решетки отклоняется только лишь в главных плоскостях.
Реализуемое фазовое распределение, а также распределение коммутационных фазовых ошибок в решетке для произвольного направления луча могут быть найдены по формулам (3.15), (3.20) или графическим способом.
В том случае, когда начальное и требуемое фазовые распределения являются функцией одной координаты например X, графическое построение рассматриваемое фазового распределения в решетке и распределения ком мутационных фазовых ошибок может быть выполнено следующим образом. Вначале строится график функции (3.15), т. е. на чертеже отмечаются фазовые сдвиги, которые могут быть реализованы в излучателях решетки. Каждому фазовому сдвигу в каком-либо излучателе соответствует определенная позиция связанного с ним коммутационного фазовращателя. График функции (3.15) при каждом значении qn имеет вид отдельных точек, которые для удобства можно соединить плавной кривой. В полученном семействе каждая кривая сдвинута относительно соседней в направлении оси ординат на величину ∆ (рис. 3.8).
Затем на этот же график наносится кривая фазового распределения, требуемого для формирования луча в заданном направлении. Фазовый сдвиг в каждом излучателе или позиция соответствующего фазовращателя
|
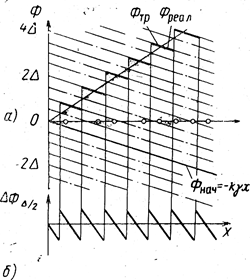
| Рис. 3.8. Реализуемое фазовое распределение (а) и распределение фазовых ошибок в коммутационной решетке (б). |
выбирается так, чтобы разность между реализуемым и требуемым фазовым распределением была наименьшей. Из графика видно, что максимальная величина фазовых ошибок при данном способе фазирования не превышает половины дискрета изменения фазы. Если излучатели в решетке расположены настолько близко, что их распределение можно рассматривать как непрерывное, то график реализуемого фазового распределения принимает вид ступенчатой кривой (рис. 3,8). Функция распределения фазовых ошибок имеет при этом пилообразный вид (рис. 3.8, б).
Сказанное выше относится как к линейным, так и к плоским коммутационным решеткам при условии, что луч плоской решетки находится в одной из главных плоскостей, а начальное фазовое распределение является функцией одной координаты.
Если начальное и требуемое фазовые распределения являются функциями двух переменных, то точки, соответствующие реализуемым значениям фазы, в решетке располагаются на семействе поверхностей, определяемом уравнением (3.15). Уравнения (3.14) определяет плоскость, положение которой зависит от требуемого направления луча и выбора точки начала отсчета фазы. Позиции фазовращателей в решетке, обеспечивающие формирование луча в заданном направлении, определяются, как и прежде, по наименьшему уклонению реализуемого фазового распределения от требуемого. В том случае, когда излучающие элементы решетки расположены настолько близко, что их можно считать непрерывно распределенными, геометрический образ реализуемого фазового распределения имеет вид «ступенчатой» поверхности, функция δΦ (х, у) - вид «гофрированной плоскости».
Диаграмма направленности коммутационной решетки может быть найдена путем суммирования полей отдельных излучателей
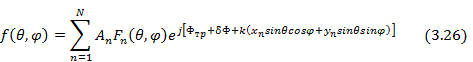
Здесь 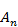 - амплитудный коэффициент n-го излучателя;
- амплитудный коэффициент n-го излучателя; 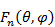 - нормированная диаграмма направленности излучателя решетки.
- нормированная диаграмма направленности излучателя решетки.
Однако расчет по формуле (3.26) при большом числе излучателей оказывается достаточно трудоемким. Кроме того, не выполнив детального расчета всей диаграммы направленности, из формулы (3.26) нельзя определить направление и уровень дополнительных боковых лепестков, обусловленных коммутационными фазовыми ошибками. Более удобны выражения, которые могут быть получены из (3.26) с помощью метода суммирования Пуассона. Для линейных и плоских решеток с линейным начальным распределением указанные выражения имеют соответственно следующий вид:
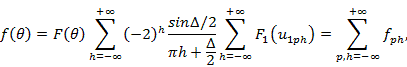
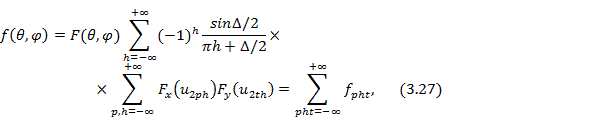
где
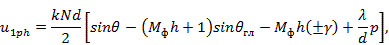
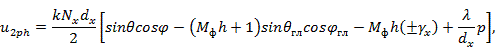
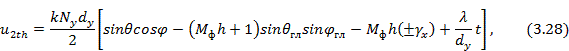
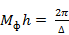 - число позиций фазовращателя.
- число позиций фазовращателя.
В зависимости от положения точки начала отсчета фазы величины F1, Fx, Fy определяются следующими выражениями:
Линейные решетки (см. рис. 3.5). Начало отсчета фазы совпадает с крайним излучателем, расположенным в точке 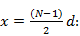
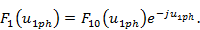
Начало отсчета фазы совпадает с серединой линейной решетки:
N — четное F1 (u1ph) = F10 (u1ph),
N — нечетное F1 (u1ph) = (-1)p F10(u1ph).
Плоские решетки (см. рис. 3.6). Начало отсчета фазы совпадает с пересечением диагоналей прямоугольника, в пределах которого расположены излучатели:
Nx — четное Fx (u2ph) = Fx0 (u2ph),
Nx — нечетное Fx (u2ph) = (-1)p Fx0(u2ph).
Ny — четное Fy (u2ph) = Fy0 (u2th),
Ny — нечетное Fy (u2th) = (-1)t Fy0(u2th).
Начало отсчета фазы совпадает с крайним излучателем, расположённым в вершине прямоугольника с координатами:
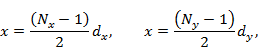
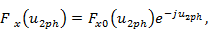
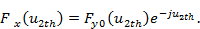
В приведенных формулах величина F10 является нормированной диаграммой направленности линейной антенны без коммутационных фазовых ошибок с непрерывным распределением излучателей и амплитудным распределением, тождественно совпадающим с амплитудным распределением в решетке. Если распределение амплитуд в коммутационной решетке совпадает с одним из распределений, приведенных в табл. 3.1, то функция F10 может быть взята из соответствующего столбца указанной таблицы.
Величины Fx0, Fy0 также являются нормированными диаграммами направленности линейных антенн без коммутационных фазовых ошибок с амплитудным распределением, совпадающим соответственно с законом изменения амплитуд возбуждения излучателей в плоской решетке вдоль координат X, Y.
Главный лепесток диаграммы направленности коммутационной решетки определяется членом рядов (3.27) с индексами h=p=t =0. Наличие членов с индексами h=0, р, t обусловлено дискретным характером распределения излучателей. В том случае, когда расстояние между излучателями не превышает максимально допустимое значение, указанные члены практически не влияют на форму диаграммы направленности решетки и их можно не учитывать. Существование остальных членов рядов (3.27) связано с наличием коммутационных фазовых ошибок.
Из формул (3.27), (3.28) следует, что диаграмма направленности коммутационной решетки представляет собой сумму ряда однотипных диаграмм направленности F1, Fx, Fy с различным направлением и уровнем максимумов. Направление максимумов определяется уравнениями
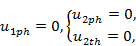
из которых получаем
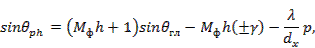
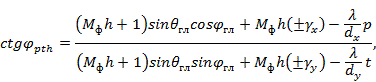
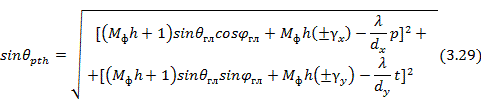
Первая формула соответствует онной решетке; две другие — плоской.
Уровни максимумов указанных диаграмм направлен ности определяются множителем вида
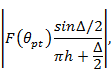
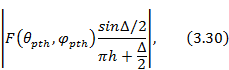
где 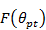 ,
, 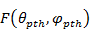 — значение диаграммы направленности элемента решетки в направлении
— значение диаграммы направленности элемента решетки в направлении 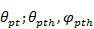 .
.
Можно показать, что член рядов (3.27) с индексами p=t=h=0 является диаграммой направленности эквивалентной антенны без коммутационных фазовых ошибок и с непрерывным распределением излучателей. В дальнейшем члены указанных рядов с индексам h≠0 и h=0 будут называться соответственно коммутационными и дифракционными лепестками. Если максимумы дифракционных лепестков находятся в области действительных углов, то диаграмма направленности коммутационной решетки имеет вторичные главные максимумы. Как уже отмечалось, в правильно сконструированной решетке вторичные главные максимумы отсутствуют, так как направления максимумов дифракционных лепестков лежат вне пределов действительных углов. Для них выполняются условия
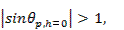 |
| 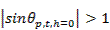 .
.
Наличие коммутационных фазовых ошибок приводит к снижению/уровня 'главного максимума диаграммы направленности антенны, которое согласно (3.27) определяется множителем 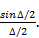 Уровень коммутационных лепестков, отнесенный к максимуму диаграммы направленности эквивалентной антенны без коммутационных фазовых ошибок и с непрерывным распределением излучателей (член рядов (3.27) с индексами p=t=h=0), равен
Уровень коммутационных лепестков, отнесенный к максимуму диаграммы направленности эквивалентной антенны без коммутационных фазовых ошибок и с непрерывным распределением излучателей (член рядов (3.27) с индексами p=t=h=0), равен
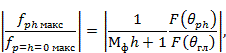
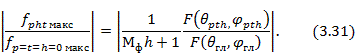
Наибольший уровень имеют коммутационные лепестки с индексами h=±1. При Δ→0, т. е. при переходе к антенне с плавными фазовращателями, 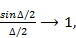 а уровни коммутационных лепестков стремятся к нулю.
а уровни коммутационных лепестков стремятся к нулю.
При расчете диаграммы направленности коммутационных решеток в большинстве случаев достаточно просуммировать те члены рядов (3.27), у которых |h|≤2 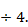 Значения индексов p, t указанных членов находятся из неравенств
Значения индексов p, t указанных членов находятся из неравенств
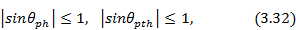
в которых величины 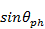 ,
,  определяются выражениями (3.29). При выполнении неравенств (3.32) максимумы коммутационных лепестков лежат в области действительных углов.
определяются выражениями (3.29). При выполнении неравенств (3.32) максимумы коммутационных лепестков лежат в области действительных углов.
Коммутационные лепестки суммируются с диаграммой направленности эквивалентной непрерывно возбужденной антенны без коммутационных фазовых ошибок и образуют дополнительные боковые лепестки диаграммы направленности решетки, обусловленные дискретным характером работы фазовращателей.
Суммируемые члены рядов (3.27), если их рассматривать как функции углов θ, φ, имеют явно выраженный главный лепесток, направление максимума которого определяется формулами (3.29). При численных расчетах дополнительных боковых лепестков, обусловленных коммутационными фазовыми ошибками, каждый из суммируемых членов в (3.27) достаточно рассчитать в пределах соответствующего главного лепестка. Если при h=±l направление максимумов 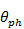 ,
, 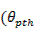 ,
, 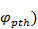 коммутационных лепестков отличается от направления
коммутационных лепестков отличается от направления 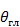 ,
, 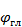 не менее чем на три-четыре ширины основного лепестка решетки, то формулы (3.29), а также выражение (3.31) с достаточной степенью точности определяют направленние и уровень дополнительных боковых лепестков диаграммы направленности коммутационных линейных и плоских решеток.
не менее чем на три-четыре ширины основного лепестка решетки, то формулы (3.29), а также выражение (3.31) с достаточной степенью точности определяют направленние и уровень дополнительных боковых лепестков диаграммы направленности коммутационных линейных и плоских решеток.
Наличие дополнительных боковых лепестков, обусловленных коммутационными фазовыми ошибками, является недостатком решеток рассматриваемого типа. Одним из очевидных способов снижения их уровня является уменьшение величины дискрета изменения фазы Д путем использования более сложных многопозиционных фазовращателей.
Из теорий коммутационных решёток следует, что уровень указанных лёпестков может быть уменьшен за счет нарушения периодичности распределения коммутационных фазовых ошибок. В рассмотренных выше коммутационных решетках периодический характер распределения коммутационных фазовых ошибок обусловлен линейными начальным и требуемым фазовыми распределениями. Периодичность коммутационных фазовых ошибок может быть устранена путем создания нелинейных начальных фазовых распределений.
Нелинейные начальные фазовые распределения реализуются различными способами. Например, в линейных решетках с последовательной схемой распределения мощности нелинейное начальное фазовое распределение между излучателями может быть создано изменением фазовой скорости волн, распространяющихся в питающем фидере. Нелинейный характер начального фазового распределения имеет место при квазиоптической схеме питания (см. рис. 3.4), когда начальное фазовое распределение является приблизительно квадратичной функцией координат (3.18), (3.19).
При квадратичном изменении начального фазового распределения величины F10, Fx0, Fy0 определяются следующими выражениями:
Равномерное амплитудное распределение в решетке
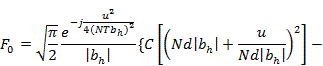
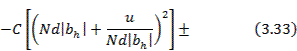
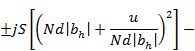
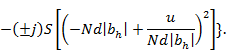
Косинусоидальное амплитудное распределение в решетке
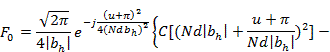
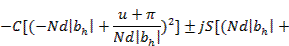
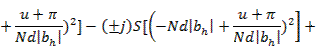
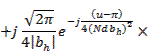
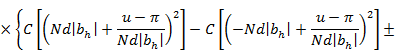
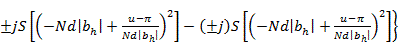 , (3.34)
, (3.34)
где S(z), С (z) — интегралы Френеля; bh = a 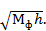 Знак «плюс» в (3.33), (3.34) соответствует индексу h>0, знак «минус» - индексу h<0.
Знак «плюс» в (3.33), (3.34) соответствует индексу h>0, знак «минус» - индексу h<0.
В приведенных формулах использованы следующие обозначения:
Линейные решетки
F1=F10=F0, u=u1ph.
Плоские решетки
Fx=Fx0=F0, u=u2ph,
d==dx, N=Nx; Fy=Fy0=F0,
u=u2th, d=dy, N=Ny.
Величины u1ph, u2ph, u2th определяются выражениями (3.28), в которых необходимо положить γ=γx=γy = 0.
Выражения (3.23), (3.24) соответствуют начальному фазовому распределению такого вида:
Линейные решетки
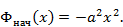
Плоские решетки
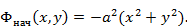
Предполагается, что точка начала отсчета фазы находится в середине линейной решетки и в точке пересечения диагоналей прямоугольника, внутри которого размещаются излучатели плоской решетки.
Степень подавления коммутационных лепестков увеличивается с ростом величины а2.
Например, для схем квазиоптического типа согласно (3.18), (3.19) имеем
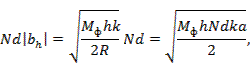
где 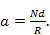
Поскольку обычно а==0,6 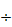 1, то из выражения (3.35) следует, что при увеличении размеров раскрыва решетки с указанной схемой распределения мощности коммутационные лепестки, а следовательно, и дополнительные боковые лепестки диаграммы направленности, уменьшаются.
1, то из выражения (3.35) следует, что при увеличении размеров раскрыва решетки с указанной схемой распределения мощности коммутационные лепестки, а следовательно, и дополнительные боковые лепестки диаграммы направленности, уменьшаются.
3.5. Скачки луча коммутационной решетки
Главный максимум диаграммы направленности эквивалентной антенны без коммутационных фазовых ошибок ориентирован точно в заданном направлении θгл. При наличии в непосредственной близости от него коммутационных лепестков максимум их суммы, т. е. максимум диаграммы направленности решетки, несколько смещается относительно направления θгл. Это смещение, обусловленное коммутационными фазовыми ошибками, определяет погрешность установки луча решетки в заданном направлении. Величина погрешности зависит от уровня коммутационных лучей и, следовательно, от дискрета изменения фазы Δ. Кроме того, на точность установки луча влияет положение точки начала отсчета фазы. Так, например, при выборе в качестве начальной точки координаты одного из крайних излучателей линейной решетки точность установки луча оказывается в четыре раза выше по сравнению с положением отсчета фазы в центре решетки [ЛО 10].
Точность установки луча непосредственно связана с его скачкообразным движением, обусловленным ди| скретным изменением фазы. Средняя величина скачка при расположении начальной точки в центре решетки
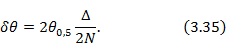
Необходимо также отметить, что при одной и той же скорости движения луча частота переключений крайних фазовращателей будет различной, в зависимости от положения точки начала отсчета фазы [ЛО 10]. Это следует учитывать при оценке необходимого быстродействия фазовращателя.
3.6. Коммутационные фазовращатели
Основным элементом антенн рассматриваемого типа являются коммутационные фазовращатели. В остронаправленных сканирующих решетках их количество может достигать несколько десятков тысяч штук. При этом расстояние между фазовращателями обычно лежит в пределах 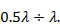
Коммутационные фазовращатели должны иметь высокий к. п. д., достаточную электрическую прочность, стабильность характеристик и потреблять минимальную мощность, необходимую для управления их работой.
Кроме того, предъявляются следующие требования к конструктивным характеристикам фазовращателей:
1. Простота конструкции и технологичность. 2. Малые габариты и вес. 3. Надежность.
Управляемые элементы фазовращателей, обеспечивающие изменение фазы, могут быть выполнены на основе ферритов, сегнетоэлектриков, устройств, в которых используется газовый разряд, и полупроводников.
Описание некоторых типов фазовращателей имеется в [ЛО 9, ЛО 10].
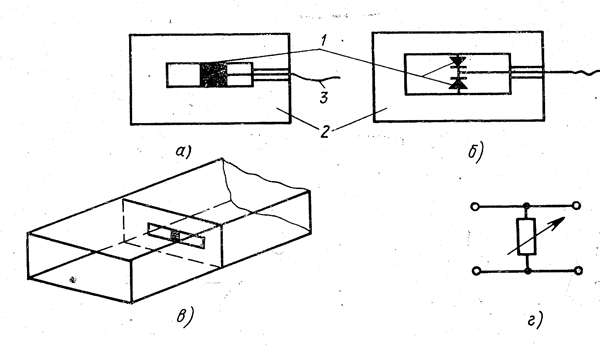
Ниже дается описание конструкций коммутационных фазовращателей сантиметрового диапазона волн, управляемым элементом которых является резонансная щель, коммутируемая pin-диодом. Свойства диодов указанного типа описаны в [Л 4].
|
| Рис. 3.9. Коммутируемая резонансная щель: а щелевой модуль; б — схема включения pin-диодов; в — волноводный коммутатор СВЧ мощности; г - эквивалентная схема волноводного коммутатора. |
Наличие диода эквивалентно включению в центре щели некоторой емкости. Поэтому для настройки в резонанс щель необходимо укоротить. Это укорочение в среднем составляет примерно 25% от резонансной длины щели без диода.
Полупроводниковые диоды размещают попарно между краями щели в соответствии со схемой, представленной на рис. 3.9,6. Подобная Щель с диодами, прорезанная в поперечной перегородке цилиндрического волновода (см. рис. 3.2,в), в обесточенном состоянии пропускает электромагнитную энергию, поступающую от генератора, с малыми потерями, в то время как при пропускании тока через диоды большая часть энергии падающей волны отражается обратно к генератору. В дальнейшем щель с обесточенными диодами будет называться незамкнутой, а щель по диоду которой протекает ток — замкнутой.
В качестве примера ниже приводятся характеристики резонансной щели с полупроводниковыми диодами одного из существующих в настоящее время типов. Указанные характеристики соответствуют щели, размещенной на поперечной перегородке в прямоугольном волноводе с размерами поперечного сечения 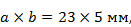 при частоте f = 9375 Мгц (λ=3.2 см). Размеры пары диодов
при частоте f = 9375 Мгц (λ=3.2 см). Размеры пары диодов 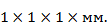 Размеры щели
Размеры щели 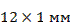 . Коэффициент прохождения в обесточенном состоянии — 0,4 дб; при пропускании тока —20 дб. Предельная пропускаемая мощность: импульсная 5 квт, средняя 10 вт. Ток управления 100 ма.
. Коэффициент прохождения в обесточенном состоянии — 0,4 дб; при пропускании тока —20 дб. Предельная пропускаемая мощность: импульсная 5 квт, средняя 10 вт. Ток управления 100 ма.
На эквивалентной схеме волновод с коммутируемой диафрагмой, о которой шла речь, изображается в виде двухпроводной линии с параллельно включенным в нее переменным активным сопротивлением (см. рис. 3.9,г), которое под действием управляющего тока может меняться от 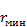 до
до 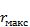 . Отношение
. Отношение

называемое «качеством», является одной из основных .характеристик полупроводниковых коммутационных диодов, определяющей свойства дискретно-коммутационных фазовращателей (к, п. д., точность установки фазы и т. д.). Существующие pin — диоды характеризуются величиной параметра К, изменяющейся в пределах 250-1000.
Одним из фазовращателей, в котором используются коммутируемые резонансные щели, является фазовращатель так называемого отражательного типа (рис. 3.10). Он состоит из закороченного на одном конце отрезка волновода, в котором на определенном расстоянии друг от друга расположены поперечные перегородки с коммутируемыми щелями. Приходящая со стороны незакороченного конца отрезка волновода электромагнитная волна, отражается от одной из перегородок с замкнутой, с помощью диода, щелью. При этом диоды в остальных перегородках обесточены. Если теперь пропустить ток через другой диод, а остальные диоды обесточить, то фаза отраженной волны на открытом конце отрезка волновода изменится из-за изменения пути, проходимого волной внутри волновода. В том случае, когда перегородки расположены на одинаковом расстоянии друг от друга, наименьшая величина скачка фазы будет равна
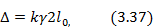
где l0 — расстояние между перегородками; γ — замедление фазовой скорости.
Выход и вход в фазовращателе рассматриваемого типа оказываются совмещёнными.
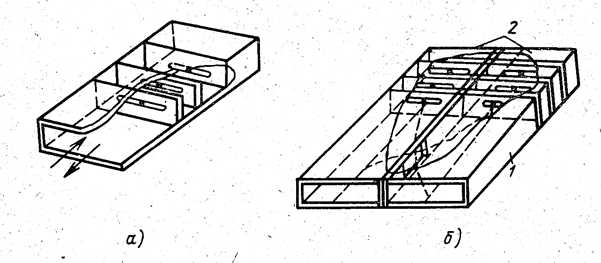
|
| Рис. 3.10. Коммутационные фазовращатели: а - отражательный; б - проходной на волноводном мосте (1 — волноводный мост; 2 — отражательные фазовращатели). |
Количество перегородок ν с коммутируемыми щелями связано с величиной Δ следующим соотношением:
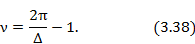
Минимальные потери в фазовращателе при Мф≤8 приближенно могут быть оценены по формуле [1]
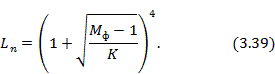
Описанный фазовращатель может быть использован как самостоятельное устройство или как отдельный узел в фазовращателе проходного типа с раздельным входом и выходом. Подобный фазовращатель состоит из трехдецибельного волноводного моста (рис. 3.10,б) и двух отражательных фазовращателей, соединенных с соответствующими плечами моста. Принцип действия трехдецибельного волноводного моста описан в [Л 2]. Подобный фазовращатель имеет механический аналог [ЛО 9], в котором отражательным фазовращателям соответствуют отрезки волноводов с подвижными короткозамыкающими поршнями. Синхронное перемещение поршней обеспечивает плавное изменение фазы на выходе фазовращателя.
В коммутационном фазовращателе синхронное переключение перегородок с диодами соответствует скачкообразному перемещению поршней в механическом аналоге.
Наименьшая величина фазового скачка в подобном фазовращателе определяется формулой (3.37), а число перегородок с коммутируемыми щелями в каждом из двух отражательных фазовращателей — формулой (3.38).
Минимальные потери в данном случае также могут быть рассчитаны по формуле (3.39).
|
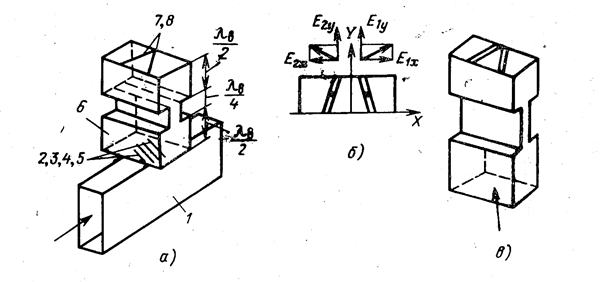
| Рис. 3.11. Коммутационный фазовращатель ответвляющего типа: а — общий вид фазовращателя; б — излучающие щели; в — проходной фазовращатель 0—π. |
Другим типом, который можно назвать «ответвляющим», является фазовращатель, изображенный на рис. 3.11. Принцип его действия состоит в следующем. В питающем волноводе 1 возбуждается бегущая волна. Через коммутируемые щели 2, 3, 4, 5 питающий волновод связан с отрезком волновода 6, в торце которого на закорачивающей стенке прорезаны наклонные щели. При работе фазовращателя всё щели связи замкнуты, кроме одной, которая возбуждает электромагнитные колебания в отрезке волновода 6. Фаза возбуждаемых колебаний зависит от номера незамкнутой щели, так как щели связи разнесены вдоль оси питающего волновода и фаза их возбуждения совпадает с фазой бегущей волны в месте расположения щелей. Для направления движения волны в питающем волноводе и нумерации щелей, показанных на рис. 3.11,а, фаза колебаний, возбуждаемых в отрезке волновода 6 незамкнутой щелью, в зависимости от номера щели равна:
щель 2 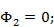 щель 3
щель 3 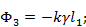
щель 4 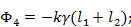
щель 5 
Энергия волны, возбуждаемой в отрезке волновода 6, излучается одной из наклонных щелей 7, 8, коммутируемых полупроводниковыми диодами. Для уменьшения поляризационных потерь угол наклона щелей берется небольшим, порядка 5-10°. Вследствие малого угла наклона преобладает по величине одна из составляющих пода щели, а именно — составляющая Ех. Указанная составляющая является рабочей. Другая составляющая поля является вредной и ее следует всячески уменьшать путем уменьшения угла наклона щелей. Составляющие поля Ех имеют противоположное направление, поэтому при переключении щелей фаза излученного поля, соответствующая компоненте Ех, изменяется на 180°. При переключении щелей связи и излучающих наклонных щелей происходит дискретное измене фазы ноля излучения. Если расстояние между щелями связи равно 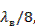 то согласно (3.40) Ф2=0, Ф3=45°, Ф4= 90°, Ф5=135°, т. е. переключение щелей связи позволяет менять возбуждение волновода 6 скачком через 45°. За счёт переключения наклонных излучающих щелей к каждому из приведенных выше фазовых сдвигов можно добавить фазовый сдвиг величиной 180°. Таким образом, данный фазовращатель обеспечивает изменение фазы скачком на 45°. Если вместо четырех щелей взять три или две щели связи и расположить их вдоль оси питающего волновода на расстоянии соответственно
то согласно (3.40) Ф2=0, Ф3=45°, Ф4= 90°, Ф5=135°, т. е. переключение щелей связи позволяет менять возбуждение волновода 6 скачком через 45°. За счёт переключения наклонных излучающих щелей к каждому из приведенных выше фазовых сдвигов можно добавить фазовый сдвиг величиной 180°. Таким образом, данный фазовращатель обеспечивает изменение фазы скачком на 45°. Если вместо четырех щелей взять три или две щели связи и расположить их вдоль оси питающего волновода на расстоянии соответственно 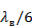 и
и 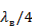 , то получим фазовращатели с изменением фазы скачком на 60 и 90°. Количество коммутируемых щелей фазовращателя данного типа равно
, то получим фазовращатели с изменением фазы скачком на 60 и 90°. Количество коммутируемых щелей фазовращателя данного типа равно
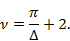
Отрезок волновода 6 с уменьшенным размером узкой стенки является четвертьволновым трансформатором. Величина его коэффициента трансформации, а также угол наклона щелей связи выбираются из условия получения максимальной величины к. п. д. и требуемой величины связи с питающим волноводом.
Следует отметить, что отрезок волновода 6 с наклонными щелями и четвертьволновым трансформатором можно использовать как самостоятельный проходной фазовращатель с дискретом изменения фазы 180°. В этом случае величина коэффициента трансформаций определяется из условия согласования.
Минимально достижимые потери в описанном выше фазовращателе определяются формулой (3.39)
3.7. Конструктивные схемы коммутационных решеток
Одним из простейших типов коммутационных решеток является решетка, составленная из отражательных фазовращателей (рис. 3.12) и облучаемая первичным облучателем.
Другим типом коммутационных решеток, в которых используются отражательные фазовращатели, является решетка, изображенная на рис. 3.13.
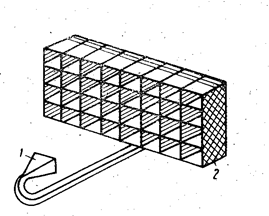
|
| Рис. 3.12: Коммутационная отражательная решетка: 1 — рупорный облучатель; 2 — отражательная решетка. |
Данная решетка соответствует последовательной схеме распределения энергии с параллельным включением фазовращателей. Характерной особенностью в данном случае является использование направленных элементов связи — крестообразных щелей 2. За счет направленной связи извлечённая из питающего волновода 1 энергия направляется в сторону отражательного фазовращателя 3, а затем излучается через открытый конец волновода. При этом некоторая часть энергии попадает обратно в питающий волновод. Величина связи каждого излуча-
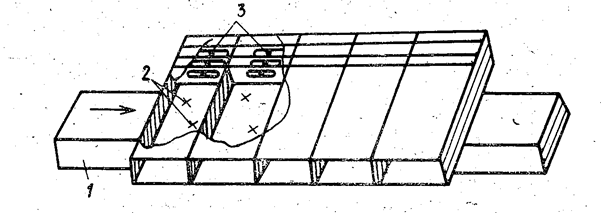
|
| Рис. 3.13. Отражательные фазовращатели в коммутационной решетке с последовательным распределением мощности СВЧ. |
теля-фазовращателя зависит от требуемого амплитудного распределения и определяется по формулам (3.2). Принцип действия крестообразного направленного ответвителя описан в [Л. 3].
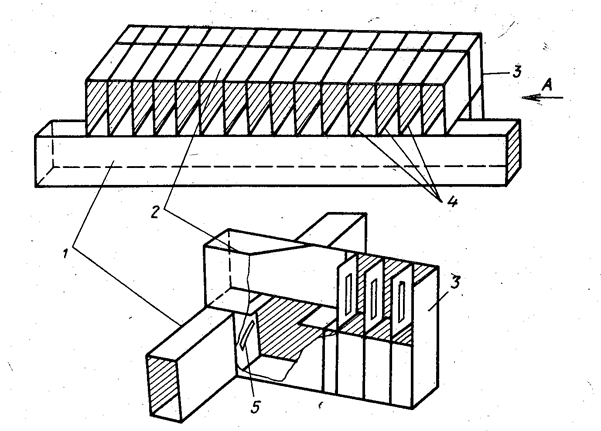
|
| Рис. 3.14. Коммутационная решетка с фазовращателями на волноводных мостах: 1 — питающий волновод; 2 — волноводные мосты; 3—отражательные фазовращатели; 4 — излучатели открытые концы волноводов; 5 — элементы связи. |
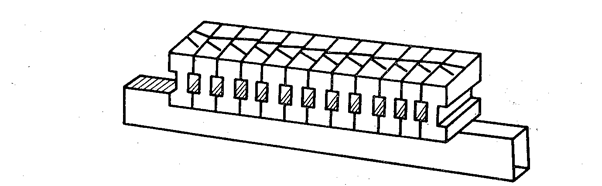
|
| Рис. 3.15. Линейная коммутационная решетка с фазовращателями ответвляющего типа. |
Решетка с проходными фазовращателями на волноводных мостах представлена на рис. 3.14. В качестве элементов связи здесь могут быть использованы круглые отверстия, щели и т. д.
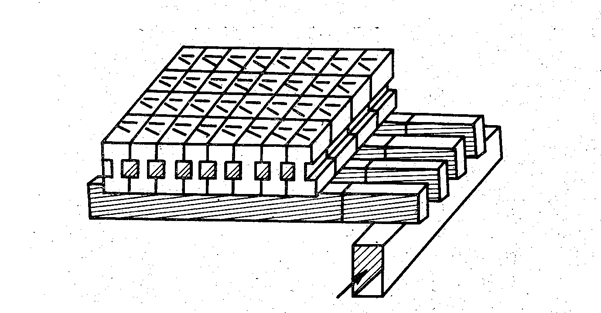
|
| Рис. 3.16. Плоская коммутационная решетка с фазовращателями ответвляющего типа. |
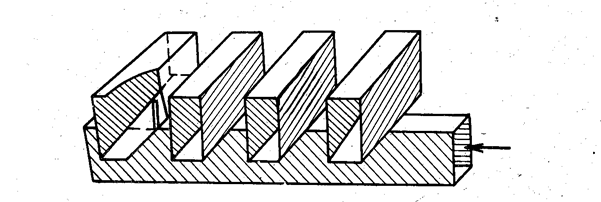
|
| Рис. 3.17. Распределитель плоской коммутационной решетки. |
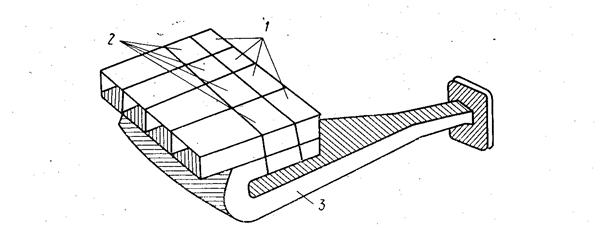
|
| Рис. 3.18. Коммутационная решетка с фазовращателями на волноводных мостах и распределителем в виде свернутого рупора: 1 — отражательные фазовращатели; 2 - волноводные мосты; 3 — свернутый рупор. |
Отличительной особенностью коммутационных решеток с фазовращателями ответвляющего типа (рис. 3.15) является то, что питающий фидер используется не только для распределения энергии между излучателями, но и для создания управляемых фазовых сдвигов, так как он является неотъемлемой частью фазовращателя.

|
| Рис. 3.19. Плоская сканирующая антенная решетка. |

|
| Рис. 3.20. Антенная система с плоской сканирующей решеткой в качестве вспомогательного зеркала. |
Из линейных решеток, изображенных на рис. 3.14, 3.15, можно набрать плоские двумерные решетки. На рис. 3.16 показана плоская решетка с фазовращателями ответвляющего типа, набранная из отдельных линейных решеток. Распределение энергии между линейными решетками осуществляется с помощью резонансного распределителя 2, который состоит (рис. 3.17) из отрезков волноводов, закороченных с одного конца и связанных через резонансные щели с питающим волноводом, также закороченным с одного конца. Расстояние в отрезках волноводов от закороченных стенок до щели связи и от центра последней щели до закорачивающей стенки питающего волновода разветвителя 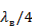 . Размеры питающего волновода выбираются такими, чтобы расстояние между щелями связи в питающем волноводе было равно половине длины волны в этом волноводе. Поворот щелей связи относительно осевой линии питающего волновода выбирается из условия согласования и получения требуемого амплитудного распределения.
. Размеры питающего волновода выбираются такими, чтобы расстояние между щелями связи в питающем волноводе было равно половине длины волны в этом волноводе. Поворот щелей связи относительно осевой линии питающего волновода выбирается из условия согласования и получения требуемого амплитудного распределения.
Для распределения энергии между линейными решетками может быть использован также свернутый рупор.
На рис. 3.18 показана коммутационная решетка квазиоптического типа с проходными фазовращателями на
| Рис. 3.21. Макет 9-элементной сканирующей решетки из керамических стержневых излучателей: а - стержневая антенна; б – подстроечный статический фазовращатель; в — управляемый фазовращатель; г – распределитель мощности. | 
|
волноводных мостах. Облучателем решетки в данном случае является секториальный рупор. Другие конструкции коммутационных решеток представлены на рис. 3.19- 3.21.
3.8. Порядок расчета
Обычно бывают заданными к. н. д. или ширина диаграммы направленности, сектор сканирования, уровень боковых лепестков и точность установки луча.
Заданная величина уровня боковых лепестков и требуемая точность установки луча определяют величину дискрета изменения фазы, т. е. число позиций фазовращателей, и амплитудное распределение в решетке.
По заданным значениям к. н. д. или ширины диаграммы направленности, выбранному амплитудному распределению, а также величине сектора, сканирования с помощью формул табл. 3.1, а также (3.3), (3.4) определяются размеры антенны. По величине сектора сканирования по формулам (3.7)—(3.9) находится расстояние между излучателями и число фазовращателей.
При определении числа позиций диекретно-коммутационных фазовращателей по максимальному уровню боковых лепестков целесообразно представить заданное значение уровня боковых лепестков в виде суммы двух слагаемых, одно из которых принимается за максимальный уровень коммутационных лепестков, а другое — за уровень боковых лепестков антенны без коммутационных фазовых ошибок. Тогда по величине первого слагаемого по формулам (3.29), (3.31) можно будет определить Δ, по величине второго - характер амплитудного распределения в решетке согласно данным табл. 3.1.
Максимальный уровень коммутационных лепестков выбирается таким, чтобы число требуемых позиций 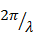 фазовращателя было меньшим. Это позволяет использовать наиболее простые по конструкции фазовращатели. С другой стороны, нельзя брать слишком малым второе слагаемое, т. е. уровень боковых лепестков идеальной антенны, так как в антенне потребуется использовать резко спадающие к краям распределения амплитуд, что приведет к необходимости увеличить размеры решетки для обеспечения заданной ширины диаграммы направленности или величины к. н. д.
фазовращателя было меньшим. Это позволяет использовать наиболее простые по конструкции фазовращатели. С другой стороны, нельзя брать слишком малым второе слагаемое, т. е. уровень боковых лепестков идеальной антенны, так как в антенне потребуется использовать резко спадающие к краям распределения амплитуд, что приведет к необходимости увеличить размеры решетки для обеспечения заданной ширины диаграммы направленности или величины к. н. д.
В зависимости от конкретных требований к антенной решетке в каждом случае находится компромиссное решение.
Далее выбирается схема распределения энергии и включения фазовращателей, тип фазовращателей, излучателей, элементов связи и т. д., производится расчет этих узлов, диаграммы направленности и разрабатывается конструкция.
Литература
1. «Современные проблемы антенно-волноводной техники». Сб. статей под ред. А. А. Пистолькорса. Изд-во «Наука», 1967.
2. Власов В. И., Берман В. И. Проектирование высокочастотных узлов радиолокационных станций. Судпромгиз, 1961.
3. Фрадин А. 3., Рыжков К. В. Измерение параметров антенн. Государственное издательство литературы по вопросам связи и радио, 1962.
4. «Устройства СВЧ с полупроводниковыми приборами». Проектирование и расчет. Под ред. Мальского И. В. и Сестрорецкого Б. В. Изд-во «Советское радио», 1969.
Глава 4
Дата добавления: 2014-12-24; просмотров: 3113;
