Суждение об устойчивости системы по ЛЧХ прямого канала и обратной ЛЧХ канала обратной связи
Об устойчивости замкнутой САУ можно судить по расположению ЛЧХ встречно-параллельных соединяемых звеньев, не прибегая к непосредственному построению ЛЧХ САУ в разомкнутом состоянии.
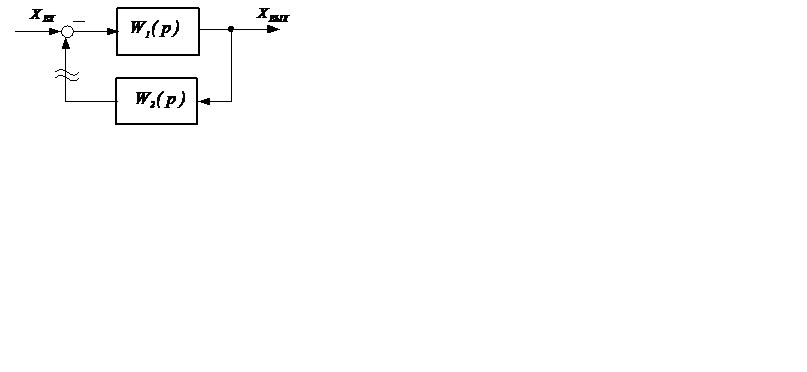
Доказано, что любая замкнутая САУ представляется в виде встречно-параллельного соединения звеньев (рисунок 5.18).
Передаточная функция разомкнутой системы равна
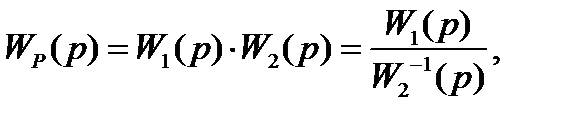(5.34)
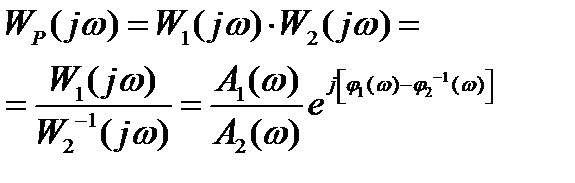Комплексный коэффициент передачи
Рисунок 5.18
. (5.35)
Для построения логарифмических амплитудно-фазовых характеристик системы автоматического управления необходимо построить характеристики L1(ω), φ1(ω), L2-1(ω), φ2-1(ω) и определить поправки. Как известно
LP(ω)= L1(ω)- L2-1(ω),
φP(ω)= φ1(ω)- φ2-1(ω), (5.36)
то есть ординаты между ЛАЧХ и ЛФЧХ прямого и обратного каналов представляют собой значения соответственно ЛАЧХ и ЛФЧХ системы в разомкнутом состоянии.
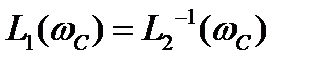Пересечения ЛАЧХ прямого и обратного каналов происходят при частоте среза, то есть , LP(ω) =0,
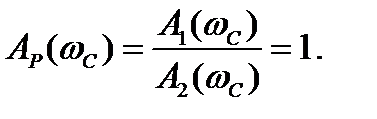
Если при LP(ω)=0, φP(ω)=180 °, то поправочная ордината АП=0
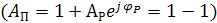и, следовательно, LП(ω)=-∞, то есть L(ω) при ω=ωС бесконечно возрастает. Таким образом, применительно к рассмотренному соединению звеньев критерий устойчивости Найквиста может быть сформулирован следующим образом.
Система автоматического управления в замкнутом состоянии устойчива, если в точке пересечения логарифмических амплитудно-частотных характеристик прямого канала и обратной амплитудно-частотной характеристики канала обратной связи разность фаз между логарифмической фазо-частотной характеристикой прямого канала и обратной логарифмической фазо-частотной характеристикой канала обратной связи меньше 180° (рисунок 5.19).
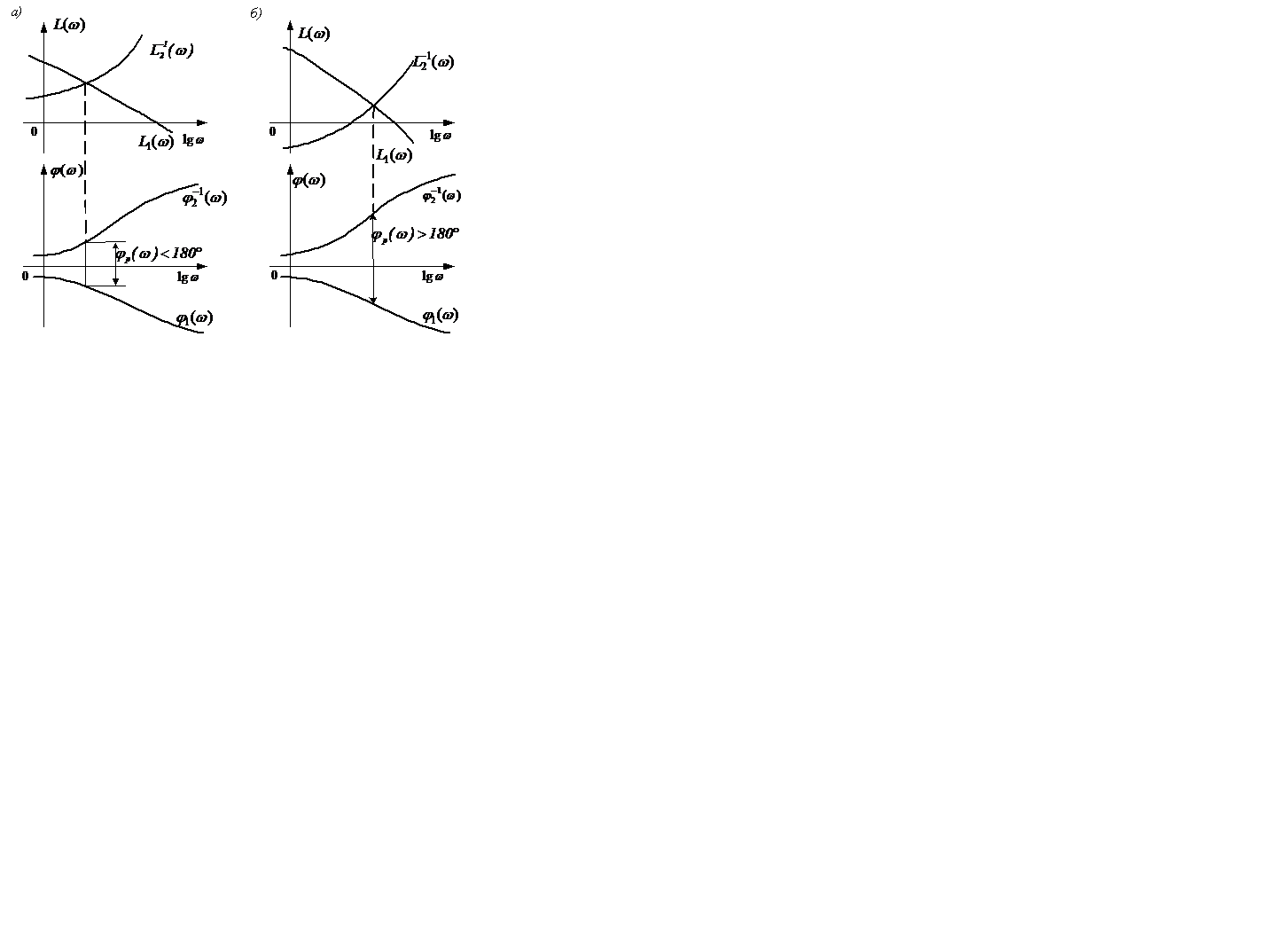
Рисунок 5.19 – Устойчивая а) и неустойчивая б) САУ
Пример 5.12. Определить устойчивость замкнутой системы вида
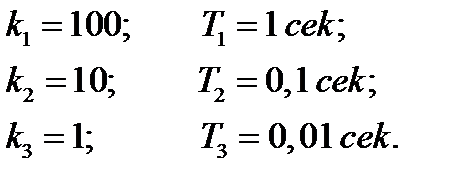Пусть
Построим ЛАФЧХ системы в разомкнутом состоянии, то есть такой системы:
Определим параметры, необходимые для построения ЛАЧХ и ЛФЧХ
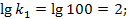
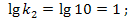
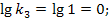
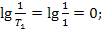
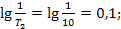
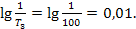
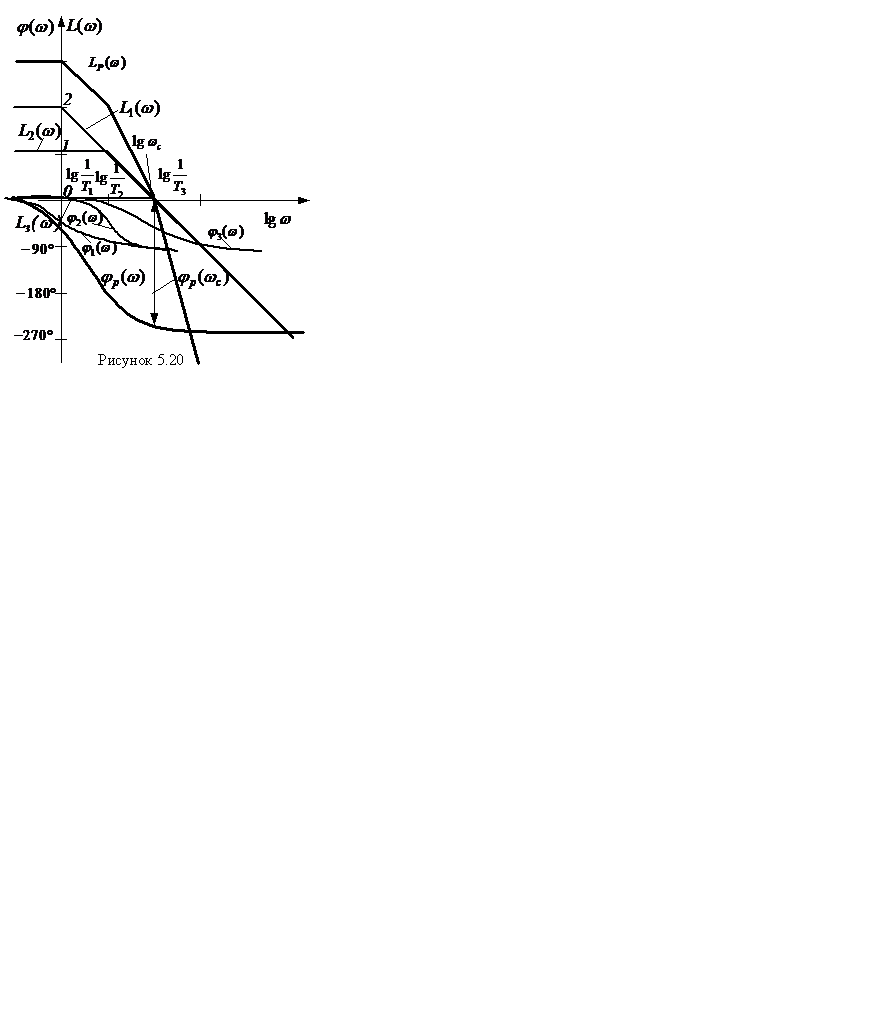
Построенные по этим данным ЛАЧХ и ЛФЧХ показаны на рисунке 5.20.
Вывод: поскольку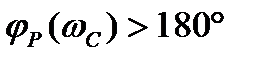 
, то система в замкнутом состоянии неустойчива.
Мы рассмотрели одноконтурную замкнутую систему. Если исследуется поведение многоконтурной САУ, то проверяют устойчивость всех контуров. А именно, строится φ1-1 , φ2-1 . Определяется, устойчив ли первый контур. Если контур устойчив, находится результирующие ЛАЧХ и ЛФЧХ этого контура. Строится L1,. L2 следующего контура и т.д. Если какой-то контур неустойчив или обладает плохими качествами переходного процесса, то вводят корректирующие устройства с тем, чтобы система имела желаемые показатели регулирования.
Дата добавления: 2014-12-22; просмотров: 696;