Суждение об устойчивости на основании критерия Найквиста по логарифмическим частотным характеристикам системы в разомкнутом состоянии
Критерий Найквиста можно использовать и по отношению к логарифмическим частотным характеристикам. Согласно критерию устойчивости Найквиста САУ устойчива, если при
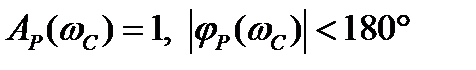. (5.32)
Если использовать логарифмический масштаб, то это означает, что
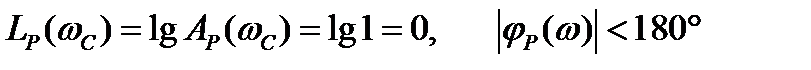. (5.33)
Условие (5.33) можно сформулировать следующим образом.
Если фазо-частотная характеристика системы в разомкнутом состоянии при частоте среза (то есть при частоте, где логарифмическая амплитудно-частотная характеристика пересекает ось абсцисс) не достигает значения
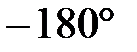, то система в замкнутом состоянии устойчива (рисунок 5.14).
Рисунок 5.14 - Система (а) устойчивая, (б) на грани
устойчивости и (в) неустойчивая
На рисунке 5.14, а показаны запасы устойчивости по фазе и по амплитуде, определённые по логарифмическим характеристикам для устойчивой системы. Для системы, находящейся на грани устойчивости Δφ=0, ΔL=0. Для неустойчивой системы запасов устойчивости не существует.
Критерий Найквиста легко можно сформулировать для логарифмических амплитудно-фазовых характеристик, используя понятия о положительных и отрицательных переходах.
Пример 5.8. Определить устойчивость системы автоматического управления, амплитудно-фазовая характеристика которой в разомкнутом состоянии равна
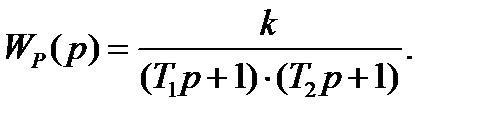
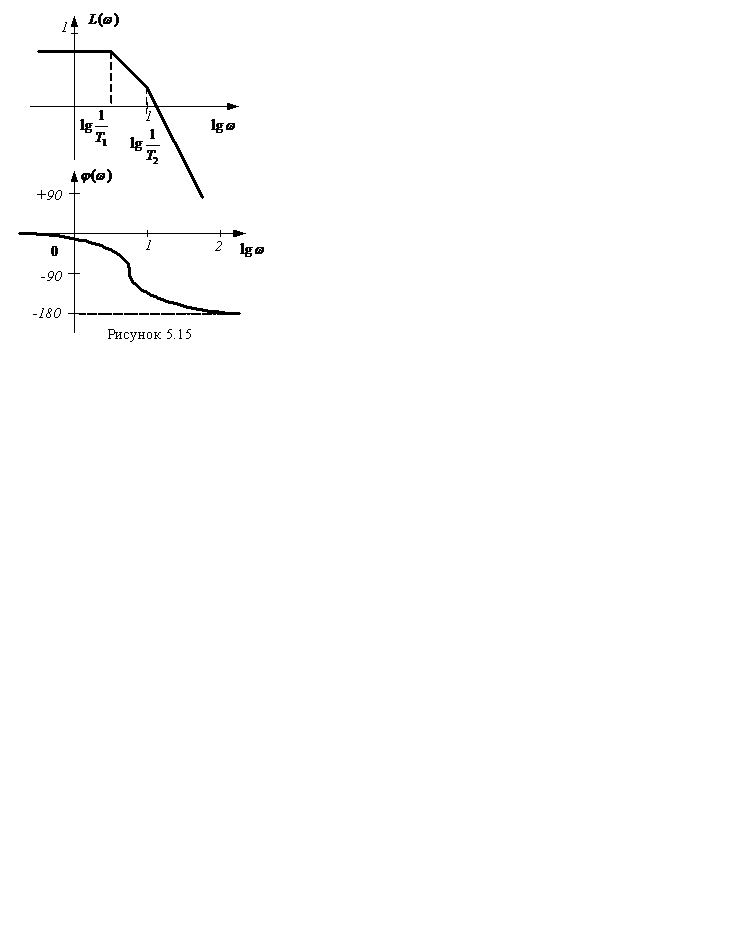
Построим логарифмические амплитудно-фазовые характеристики (рисунок 5.15).
Из этого примера видно, что если в разомкнутом состоянии имеет второй порядок (не два интегрирующих звена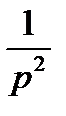 
), то при любых конечных значениях коэффициентов и постоянных времени система в замкнутом состоянии устойчива.
Пример 5.9. Определить устойчивость системы автоматического управления:
Комплексный коэффициент передачи разомкнутой системы равен
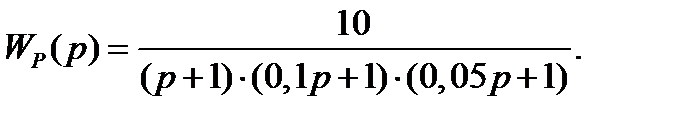
Найдём величины, необходимые для построения логарифмических амплитудно-фазовых характеристик
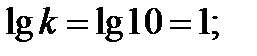
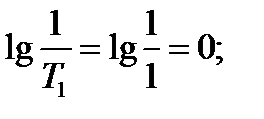
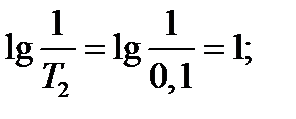
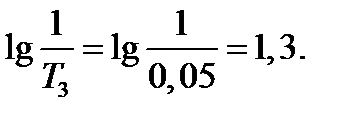
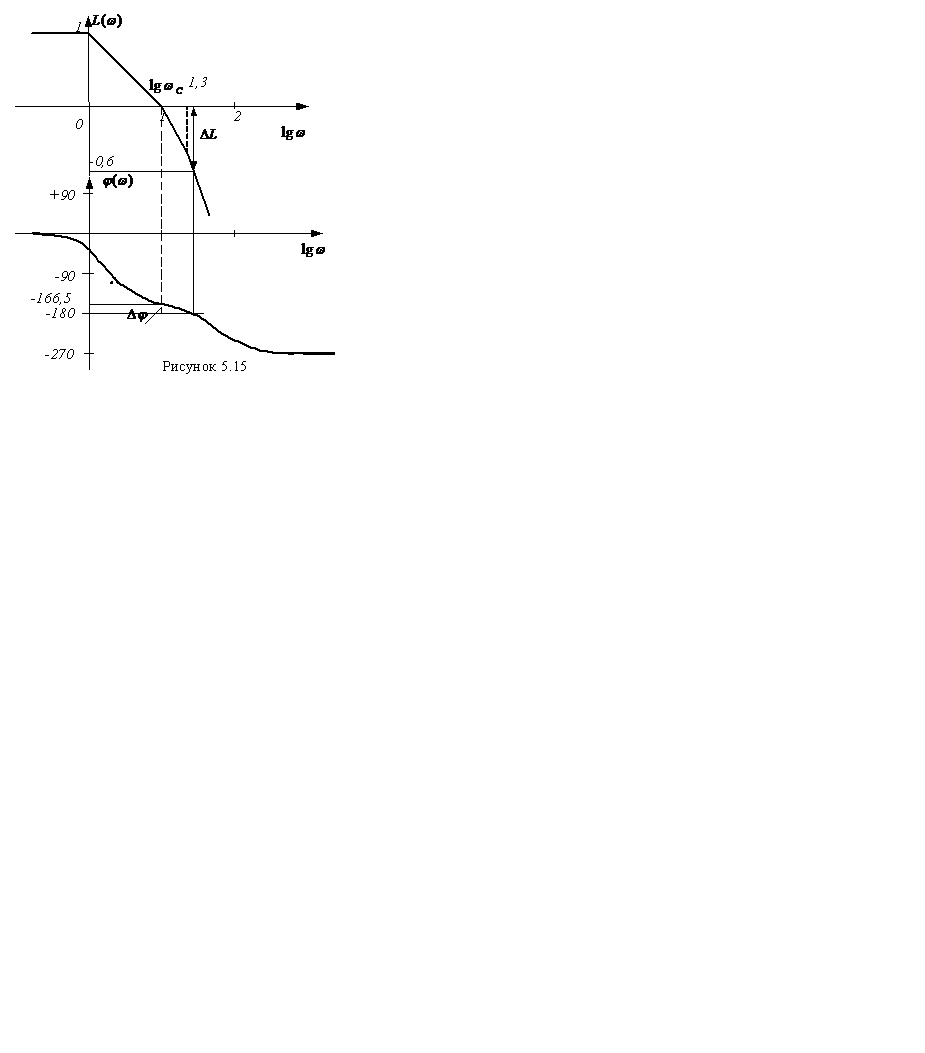
По данным построим ЛАЧХ и ЛФЧХ (рисунок 5.15).
Из рисунка найдём
|Δφ|=180°-166,5°=13,5°,
ΔL=|-0,6|.
Чем меньше ΔL, тем ближе САУ ко границе устойчивости.
По критерию Найквиста система автоматического управления устойчива.
Пример 5.10. Определить устойчивость замкнутой системы, амплитудно-фазовая характеристика которой в разомкнутом состоянии равна
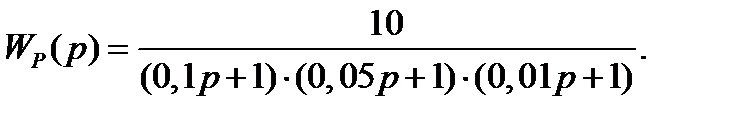
Вычислим параметры, необходимые для построения логарифмической амплитудно-фазовой характеристики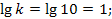 
r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
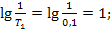ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">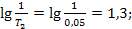 
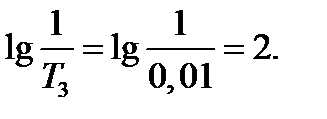
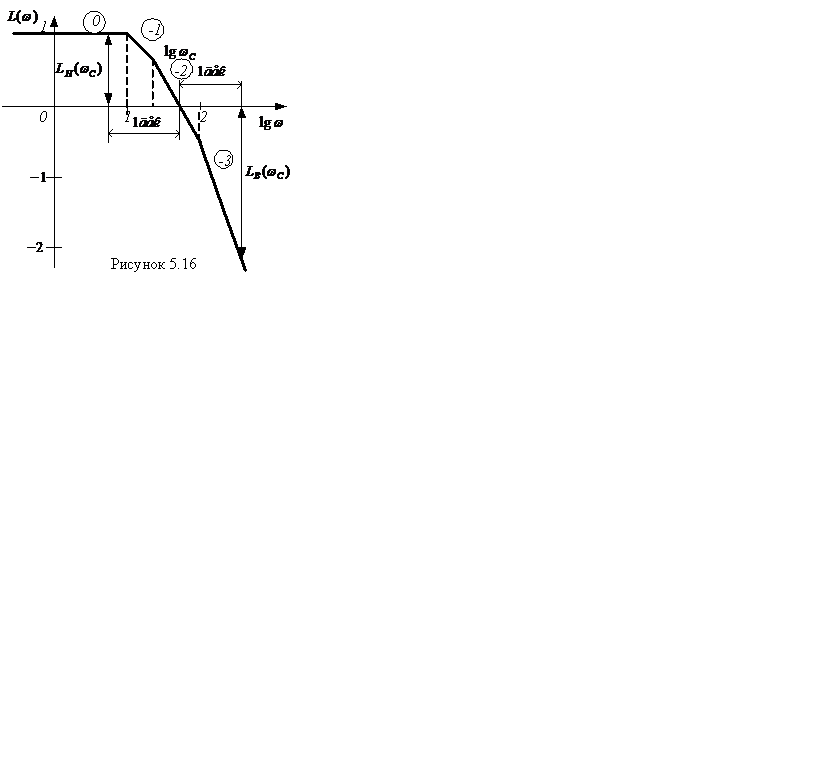
По этим данным построим ЛАЧХ (рисунок 5.16).
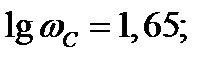Из геометрических соображений найдём частоту среза системы: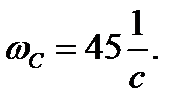 
От этой частоты отложим 1дек влево, 1дек вправо. По характеристике вычислим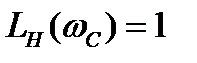 
и 
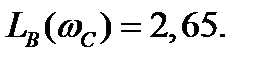
По формуле (1.28) найдём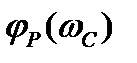 
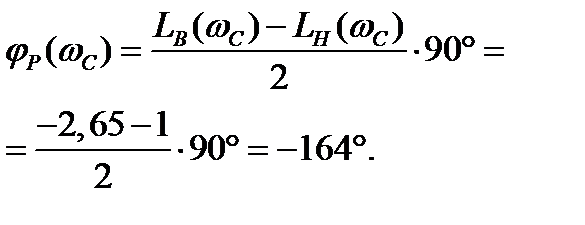
Вывод: система в замкнутом состоянии устойчива.
Пример 5.11. Определить устойчивость замкнутой системы автоматического управления
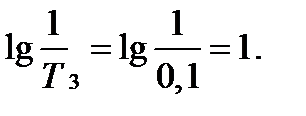
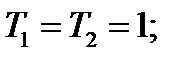
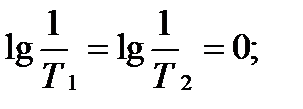Вычислим параметры, необходимые для построения логарифмических частотных характеристик
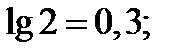
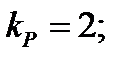
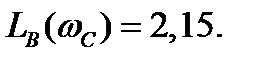
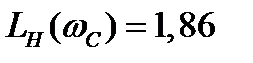
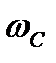
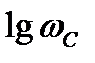По найденным данным построим ЛАЧХ и ЛФЧХ (рисунок 5.17).
По рисунку найдём и , и
По формуле (1.28) вычислим φР(ωС)
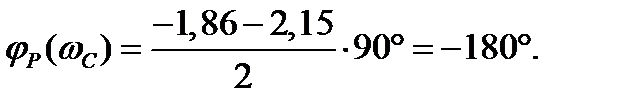
Система находится на грани устойчивости. Чтобы она была устойчивой надо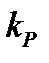 
понизить.
Вывод: чем больше 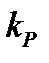система в замкнутом состоянии более колебательна или неустойчива.
В статике:
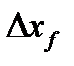- по возмущению; 
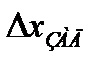- по заданию.
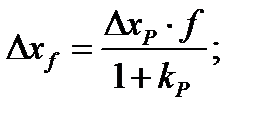
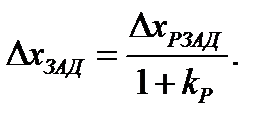
Вывод: чем выше kP , тем точнее в статике. Тем больше ΔхЗАД уменьшается.
Дата добавления: 2014-12-22; просмотров: 1314;