Трение скольжения

При стремлении сдвинуть одно тело по поверхности другого в плоскости соприкосновения тел возникает сила трения 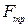(или сила сцепления), которая может принимать любые значения от нуля до значения 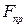, называемого предельной силой трения.

Приложенная к телу сила трения направлена в сторону, противоположную той, куда действующие на тело силы стремятся его сдвинуть.

Предельная сила трения численно равна произведению статического коэффициента трения на нормальную реакцию:

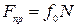
Статический коэффициент трения 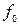— величина безразмерная; он определяется опытным путем. Значение предельной силы трения не зависит от размеров соприкасающихся при трении поверхностей.

При равновесии 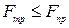или

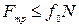
Равновесие, имеющее место, когда 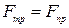, будем называть предельным равновесием.

При движении сила трения направлена в сторону, противоположную движению, и равна произведению динамического коэффициента трения на нормальное давление:

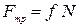
Динамический коэффициент трения скольжения 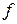также является величиной безразмерной и определяется опытным путем.

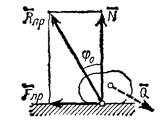Реакция реальной (шероховатой) связи слагается из двух составляющих: из нормальной реакции 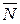и перпендикулярной ей силы трения 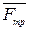. Следовательно, полная реакция 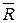будет отклонена от нормали к поверхности на некоторый угол. При изменении силы трения от нуля до 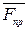сила 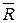изменяется от 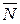до 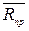, а ее угол с нормалью растет от нуля до некоторого предельного значения 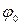.(рис.). Наибольший угол 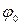называется углом трения. Из чертежа видно, что

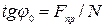
Так как 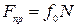, то отсюда находим следующую связь между углом трения и коэффициентом трения: .

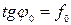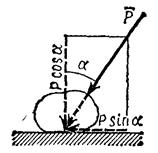
Если к телу, лежащему на шероховатой поверхности, приложить силу 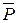, образующую угол 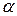с нормалью (рис.), то тело сдвинется только тогда, когда сдвигающее усилие 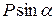будет больше 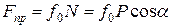. Но неравенство 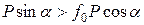, в котором 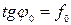, выполняется только при 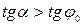, т. е. при 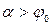. Следовательно, никакой силой, образующей с нормалью угол 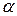, меньший угла трения 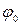, тело вдоль данной поверхности сдвинуть нельзя. Этим объясняются известные явления заклинивания или самоторможения тел.

При аналитическом решении задач с учетом силы трения реакцию шероховатой связи изображают двумя ее составляющим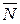и и 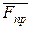. Затем составляют обычные уравнения равновесия и присоединяют к ним равенство 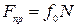(при движении тела 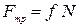) из этой системы и определяют искомые величины.