Застосування алгебри булевих функцій до релейно-контактних схем
Розглянемо електричні релейно-контакные схеми, головний елемент яких - електромагнітне реле.
Нехай x1, x2, ... , xn – набір контактів у схемі. Контакти можуть бути розмикальними й замикаючими. Контакт називається им якщо він замикається при подачі напруги. Контакт називається розмикальним, якщо він розмикається при подачі напруги. Той самий контакт у схемі може бути як замикаючим, так і розмикальної.
Кожної послідовно- паралельній схемі зіставимо функцію провідності:
f(x1, x2, ... , xn) = 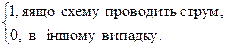
Функція провідності схеми, що складає з одного елемента x, для замикаючого контакту є f(x) = x, а для розмикального контакту f(x) = Øx.
Функція провідності схеми, що складає із двох послідовно з'єднаних контактів x й y (рис. 4.1) є f(x, y) = x&y.
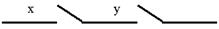
Рис. 4.1
Функція провідності схеми, що складає із двох паралельно з'єднаних контактів x й y (рис. 4.2) є f(x, y) = x V y.
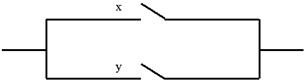
Рис. 4.2
Кожній рівнобіжній-послідовно-паралельній схемі можна поставити у відповідність формулу логіки булевих функцій, що реалізує функцію провідності цієї схеми. Дві схеми вважаються еквівалентними, якщо вони мають однакову функцію провідності. Застосовуючи рівносильні перетворення, можна спрощувати контактні, контактно-релейно-контактні схеми, заміняючи їх еквівалентними, з меншим числом контактів.
Приклад 4.22.
Знайдемо функцію провідності схеми, зображеної на рис. 4.3.
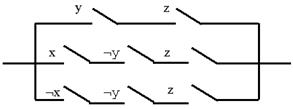
Рис. 4.3
f(x, y, z) = (y&z) V (x&Øy&z) V (Øx&Øy&z) º (y&z) V (Øy&z) º z.
Еквівалентна схема зображена на рис. 4.4.
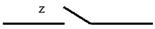
Рис 4.4
Контрольні питання до теми 4
1. Виберіть правильний варіант відповіді 1 - 4 для наступних питань:
а) Скільки існує різних булевих функцій n змінних? б) Скільки існує різних наборів змінних для булевої функції n змінних?
Варіанти відповіді: 1) 2n; 2) 22 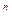 ; 3) n2; 4) n!.
; 3) n2; 4) n!.
2. Яке з наступних тверджень вірно:
а) Змінні булевої функції і сама булева функція приймають значення 0 або 1;
б) Змінні булевої функції приймають значення 0 або 1, а значення самої булевої функції збігаються із множиною дійсних чисел;
в) Значення змінних булевої функції збігаються із множиною дійсних чисел, а сама булева функція приймає значення 0 або 1;
г) Значення змінних булевої функції й значення самої функції збігаються із множиною дійсних чисел;
3. Виберіть правильний варіант відповіді 1 - 4 для наступних питань:
а) Скільки може бути різних ДНФ у булевої функції?
б) Скільки може бути різних ДДНФ у булевої функції?
в) Скільки може бути різних КНФ у булевої функції?
г) Скільки може бути різних ДКНФ у булевої функції?
Варіанти відповіді:
1 - нуль або одна; 2 - нуль або нескінченно багато; 3 - нуль або одна; 4 - одна; 5 - одна або нескінченно багато.
4. У який з нормальних форм (ДНФ, ДДНФ, КНФ, ДКНФ) перебуває дана формула булевої функції трьох змінних f(x, y, z):
а) xVy&z; б) x&y&z; в) (xVy)&(xVØz); г) xVyVz; д) Øx&y&z V y&Øz; е) xVØy; ж) x&z.
5. Яка релейно-контактна схема відповідає функції провідності f(x) = (xVy)&(xVØz)?
6. Побудувати досконалу диз’юнктивну нормальну форму
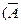 Ù
Ù 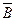 )Ù(
)Ù( 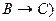 ;
;
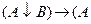 ÙC);
ÙC);
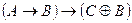 ;
;
(AÙ 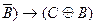 .
.
7. Записати досконалу диз’юнктивну нормальну форму бульових функцій, які приймають значення 1 тільки при таких значеннях аргументів:
(0,0),(0,1),(1,0);
(0,1,0),(1,0,0),(0,0,1);
(1,1,1,0),(1,1,0,1),(1,0,1,1),(0,1,1,1),(1,0,0,0);
(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1),(1,1,1,1);
(1,1,0,0),(1,0,0,1),(1,0,1,0),(0,1,1,0),(0,1,0,1),(0,0,1,1),(1,1,1,1).
8. Записати досконалу диз’юнктивну нормальну форму бульових функцій f1(x1,x2,x3), f2(x1,x2,x3), f3(x1,x2,x3) та f4(x1,x2,x3) які задані таблично:
| X1 | X2 | X3 | f1(x1,x2,x3) | f2(x1,x2,x3) | f3(x1,x2,x3) | f4(x1,x2,x3) |
Дата добавления: 2014-12-22; просмотров: 2394;
