Розміщення. Розміщення з повтореннями
Нагадаємо означення впорядкованої множини.
Означення 5.1.1. Множину 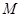 називають впорядкованою, коли в ній встановлено відношення порядку “менше”, що має такі властивості:
називають впорядкованою, коли в ній встановлено відношення порядку “менше”, що має такі властивості:
1)  : або
: або 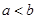 , або
, або  ;
;
2) 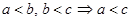 .
.
Означення 5.1.2. Нехай 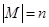 , тобто множина
, тобто множина 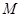 складається з
складається з 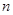 елементів,
елементів, 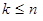
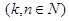 . Розміщенням без повторень з
. Розміщенням без повторень з 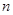 елементів по
елементів по 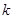 називають довільну впорядковану підмножину
називають довільну впорядковану підмножину 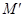 множини
множини 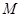
 , всі елементи якої різні.
, всі елементи якої різні.
Кількість різних розміщень з 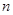 елементів по
елементів по 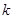 без повторень позначають:
без повторень позначають:
 .
.
Два розміщення вважають різними не лише тоді, коли вони відрізняються один від одного хоча б одним елементом, але й тоді, коли вони складаються з однакових елементів, але відрізняються порядком їх розміщення.
Теорема 5.1.1. Кількість 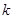 -розміщень без повторень з
-розміщень без повторень з 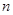 елементів
елементів 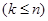 визначається так:
визначається так:
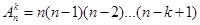 .
.
Доведення
Перший елемент впорядкованої пари 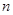 -елементної множини можна вибрати
-елементної множини можна вибрати 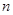 способами, другий –
способами, другий –  способами. Впорядковану пару за правилом добутку вибирають
способами. Впорядковану пару за правилом добутку вибирають 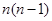 способами, впорядкована трійка –
способами, впорядкована трійка – 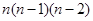 способами. Продовжуючи цей процес далі, отримаємо:
способами. Продовжуючи цей процес далі, отримаємо:
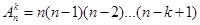 .
.
Теорему доведено. <
Теорема 5.1.2. Кількість різних розміщень без повторень з 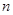 елементів по
елементів по 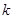 дорівнює добутку
дорівнює добутку 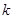 послідовних чисел, більшим з яких є
послідовних чисел, більшим з яких є 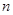 :
:
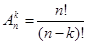 .
.
Приклад. Нехай студенту необхідно скласти чотири екзамени протягом десяти днів. Скількома способами можна це зробити?
Дата добавления: 2014-12-22; просмотров: 1576;
