Розкладання булевої функції по змінним
Нехай s приймає значення 0 або 1, тобто s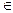 
{0, 1}.
Уведемо 
позначення:
xs = Øx, якщо s = 0, xs = x, якщо s = 1.
Т. е. x0 =Øx , x1 = x.
Очевидно, що xs = 1, якщо x = s й xs = 0, якщо x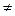 
s.
Теорема 4.2.4 (про розкладання булевої функції по змінним).
Кожна булева функція f(x1, x2, ... , xn) може бути представлена у вигляді:
f(x1, x2, ... , xn) = f(x1, x2, ... , xm, xm+1, ... , xn) = V x1s1&x2s2&...&xmsm&
f(s1, s2, ... sm, xm+1, ... , xn), (4.1)
m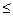 
n, де диз'юнкція береться по всіх наборах (s1, s2, ... , sm) (їх 2m).
Наприклад, для m = 2, n = 4 розкладання (4.1) містить у собі чотири (2m = 22 =4) кон’юнкції й має вигляд:
f(x1, x2, x3, x4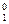) = x 
&x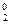 
&f(0, 0, x3, x4) V 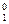x &x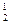 
&f(0, 1, x3, x4) V 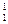x 
& x 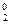&f(1, 0, x3, x4) V 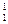x & x 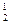&f(1, 1, x3, x4) = Øx1&Øx2&f(0, 0, x3, x4) V Øx1&x2&f(0, 1, x3, x4) V x1&Øx2&f(1, 0, x3, x4) V x1&x2&f(1, 1, x3, x4).
Доведення теореми 4.5.
Теорема буде доведена, якщо показати, що рівність (4.1) виконується для довільного набору змінних (y1, y2, ... , ym, ym+1, ... , yn) .
Підставимо цей довільний набір змінних у ліву й праву частини рівності (4.1).
У лівій частині одержимо f (y1, y2, ... , yn) .
Т. к. ys = 1 тільки, коли y = s, те серед 2m кон’юнкцій y1s1&y2s2&...&ymsm у правій частині (4.1) тільки одна звернеться в 1 – та, у якій y1 = s1,…, ym=sm... Всі інші кон’юнкції рівні 0. Тому в правій частині (4.1) одержимо:
y1y1&y2y2&...&ymym&f(y1, y2, ... , ym, ym+1, ... , yn) = f(y1, y2, ... , yn) .
Теорема 4.5 доведена.
Теорема 4.6 (про подання булевої функції формулою в ДДНФ),
Усяка булева функція f(x1, x2, ... , xn),не рівна тотожно 0, може бути представлена формулою в ДДНФ, що визначається однозначно з точністю до перестановки диз'юнктивних членів.
Доведення.
При m = n одержимо важливий наслідок теореми 4.5:
f(x1,x2,...,xn)=Vx1s1&x2s2&...&xnsn, (4.2)
f(s1, s2, ... , sn) = 1
де диз'юнкція береться по всіх наборах (s1, s2, ... , sn), на яких f = 1.
Очевидно, що розкладання (4.2) є не що інше, як ДДНФ формули f, що містить стільки кон’юнкцій, скільки одиниць у таблиці значень f. Отже, ДДНФ для всякої булевої функції єдина з точністю до перестановки її диз'юнктивних членів.
Очевидно також, що для булевої функції f(x1, x2, ... , xn), тотожно рівної 0, розкладання (2) не існує.
У силу викладеного для одержання формули булевої функції f(x1, x2, ... , xn) у ДДНФ можна скористатися наступним алгоритмом.
Алгоритм 4.3. (Алгоритм подання булевої функції, заданою таблицею, формулою в ДДНФ).
Крок 1. Вибираємо в таблиці всі набори змінних s1, s2, ... , sn, для яких значення f дорівнює 1, тобто f (s1, s2, ... , sn) = 1.
Крок 2. Для кожного такого набору (рядка таблиці) становимо кон’юнкцію x1s1&x2s2&...&xnsn, де xisi = xi, якщо si = 1 й xisi =Øxi, якщо si = 0, i = 1, 2, ... ,n.
Крок 3. Становимо диз'юнкцію всіх отриманих кон’юнкцій. У результаті вийде формула даної функції в ДДНФ.
Приклад 4.15.
Знайдемо формулу в ДДНФ для функції f(x1, x2, x3), заданою таблицею 4.4.
1. Виберемо в таблиці рядка, де f(x1, x2, x3) =1. Це 4-а, 5-а. 6-а й 8-а рядка.
2. Для кожного обраного рядка становимо кон’юнкції за правилом, зазначеному в кроці 2. Одержимо відповідно для чотирьох обраних рядків:
x10&x21&x31 = Øx1 &x2&x3.
x11&x20&x30 = x1&Øx2&Øx3.
x11&x20&x31 = x1&Øx2&x3 .
x11&x21&x31 = x1&x2&x3 .
3. Становимо диз'юнкцію всіх отриманих кон’юнкцій і знаходимо ДДНФ:
f(x1, x2, x3) = Øx1&x2&x3V x1&Øx2&Øx3 V x1&Øx2&x3 V x1&x2&x3.
Переконуємося, що це вираження збігається з отриманим раніше в прикладі 4.13 поданням нашої формули в ДДНФ.
Зауваження. Якщо булева функція задана формулою в ДДНФ, то, застосовуючи алгоритм 4.3 у зворотній послідовності, легко можемо одержати таблицю значень цієї функції.
Теорема 4.7 (про подання булевої функції формулою в ДКНФ),
Усяка булева функція f(x1, x2, ... , xn),не рівна тотожно 1, може бути представлена формулою в ДКНФ, що визначається однозначно з точністю до перестановки диз'юнктивних членів.
Доведення.
Розглянемо функцію Øf(x1, x2, ... , xn). Відповідно до теореми 4.6, якщо вона не дорівнює тотожно 0, існує її формула в ДДНФ. Позначимо цю формулу F1. Очевидно, умова, що функція Øf(x1, x2, ... , xn) не дорівнює тотожно 0, рівносильно умові, що функція f(x1, x2, ... , xn) не дорівнює тотожно 1. Крім того, за законом де Моргана формула F2 º ØF1 перебуває в ДКНФ (заперечення кон’юнкції є диз'юнкція заперечень). За законом подвійного заперечення
F2 º ØF1 º ØØf(x1, x2, ... , xn) º f(x1, x2, ... , xn),
що й доводить теорему.
Для одержання формули булевої функції f(x1, x2, ... , xn) у ДКНФ варто скористатися наступним алгоритмом.
Алгоритм 4.4. (Алгоритм подання булевої функції, заданою таблицею, формулою в ДКНФ)
Крок 1. Вибираємо в таблиці всі набори змінних s1, s2, ... , sn, для яких значення f (s1, s2, ... , sn) = 0.
Крок 2. Для кожного такого набору (рядка таблиці) становимо диз'юнкцію
x1 Øs1Vx2Øs2V...VxnØsn, де xi Øsi = xi, якщо si = 0 і xi Øsi = Øxi, якщо si = 1, i = 1, 2, ... , n.
Крок 3. Становимо кон’юнкцію всіх отриманих диз'юнкцій. У результаті вийде ДКНФ.
Приклад 4.16.
Знайдемо формулу в ДКНФ для функції f(x1, x2, x3), заданою таблицею 4.4.
1. Виберемо в таблиці рядки, де f(x1, x2, x3) = 0. Це 1-ий, 2-ий, 3-ий і 7-ий рядки.
2. Для кожного обраного рядка становимо диз'юнкції за правилом, зазначеному в кроці 2. Одержимо відповідно для трьох обраних рядків:
x11Vx21Vx31 = x1Vx2Vx3.
x11Vx21Vx30 = x1Vx2VØx3.
x11Vx20Vx31 = x1VØx2Vx3.
x10Vx20Vx31 = Øx1VØx2V x3.
3. Становимо кон’юнкцію всіх отриманих диз'юнкцій і знаходимо ДКНФ:
f(x1, x2, x3) = ( x1Vx2Vx3)&(x1Vx2VØx3)&(x1VØx2Vx3)&(Øx1VØx2Vx3).
Це вираження збігається з отриманим раніше в прикладі 4.14 поданням нашої формули в ДКНФ.
Зауваження. Т. к. усього рядків у таблиці функції 2n, те, якщо число диз'юнктивних членів у ДДНФ дорівнює p, а число конъюнктивных членів у ДКНФ дорівнює q, те p+q=2n.
Так, для функції, розглянутої в прикладах 4.15 й 4.16, n = 3, p = 4, q = 4, p + q = 8 = 23.
Дата добавления: 2014-12-22; просмотров: 5071;