МЕТОДИКА СИНТЕЗА АСИНХРОННЫХ СЧЕТЧИКОВ

В ряде случаев от счетчика требуется не высокое быстродействие, а возможно более простая схемы, имеющая меньшее число элементов, меньшую потребляемую мощность и т.д. В этом случае целесообразно использовать асинхронные счетчики.

Упрощение схемы асинхронного счетчика достигается тем, что разрешающий сигнал (положительный перепад для D триггеров, и отрицательный - для JK-триггеров) поступает на тактовые входы c триггеров не в каждом такте, как в синхронных счетчиках, а по возможности, только в те такты когда триггер должен изменять свое состояние (т.е. переключаться из 0 в 1, или наоборот).

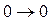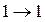В остальные такты работы, когда разряд (т.е. триггер) не изменяет своего состояния, совершая переход , или , разрешающий сигнал стремятся не подавать (а раз нет разрешения - триггер будет находиться в режиме хранения предыдущего состояния), что позволяет иметь произвольные сигналы на информационных входах триггеров. В результате упрощаются уравнения входов триггеров и, как следствие, упрощается схема счетчиков.

Методика синтеза асинхронных счетчиков в основном базируется на методе синтеза синхронных счетчиков с добавлением одного этапа и небольших изменениях в остальных, Этот синтез производится в семь этапов:

1.Определение количества разрядов счетчика по формуле 2.4 (только для двоичных кодов) и составление таблицы функционирования.

2.Определение сигналов, подаваемых на тактирующие входы триггеров.

3.Заполнение прикладных диаграмм Вейча и выделение на них ячеек, соответствующих отсутствию разрешающего сигнала на тактирующих входах триггеров.

4.Заполнение диаграмм Вейча для уравнений входов с использованием прикладных диаграмм Вейча и таблиц переходов используемых триггеров.

5.Считывание с диаграмм Вейча уравнений входов в минимизированном виде с учетом дополнительно появившихся доопределяемых значений (ячеек диаграмм).

6.Перевод уравнений входов в структурный вид в используемом базисе логических элементов.

7.Изображение схемы счетчика.

2.8 АСИНХРОННЫЙ СУММИРУЮЩИЙ ДВОИЧНЫЙ СЧЕТЧИК В КОДЕ ''4-2-1'' с К_сч=8 JK-ТРИГГЕРАХ

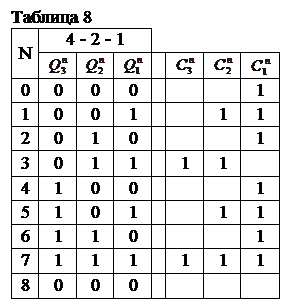1.Определяем количество разрядов, заполняем таблицу функционирования аналогично соответствующему синхронному счетчику (см. п. 2.3.)

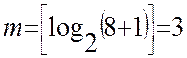
2.Определяем сигналы, подаваемые на тактирующие входы триггеров. Таблица функционирования (табл.8) дополняется справа столбцами (их количество равно числу m разрядов счетчика), в которых отображаются сигналы (функции) на тактирующих входах триггеров всех разрядов.

Условимся символом ''1'' отображать наличие разрешающего сигнала на входе С и символом ''0'' его отсутствие. Заметим, что для синхронного счетчика столбцы для сигналов С заполнились бы в каждом такте N, поскольку в нем каждый триггер в каждом такте (или при каждом появлении счетного сигнала) получает разрешающий сигнал.

При заполнении в таблице сигналов С отмечаются строки (такты) в которых разрешающий сигнал на входах С обязательно должен иметь место (С=1),как это сделано в табл.8. Разрешающий сигнал ''1'' на входе С должен быть, очевидно, тогда, когда триггер изменяет свое состояние, т.е. совершает переход 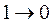или 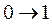. Первый разряд, как это видно из таблицы функционирования (столбец 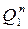) меняет свое состояние при каждом приходе счетного сигнала (в каждом такте), и поэтому в каждом такте он должен получать разрешающий сигнал. Такой сигнал имеет место только на счетном входе счетчика! Следовательно, тактирующий вход С триггера первого разряда необходимо соединить со счетным входом счетчика, как это было сделано в синхронном счетчике, и никаких отличий в нахождении уравнений входов первого разряда по сравнению с синхронным вариантом счетчика нет. Второй разряд на первом такте (при изменении состояния счетчика из 000 в 001) состояния не меняет, б т.е. триггер совершает переход 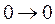, и поэтому разрешающий сигнал на вход С желательно, но не обязательно, не подавать (С=0). На втором такте((табл.8),N=1) происходит изменение состояния триггера, и для этого на его вход С необходимо подать разрешающий сигнал. Аналогично анализируются остальные такты работы и другие разряды. Для простоты, чтобы не загромождать таблицу 8, строки, соответствующие С=0 можно оставлять пустыми.

Заметим, что если бы удалось найти внутри схемы именно такие сигналы для входов (с минимальным числом дополнительных логических элементов). Однако это удается далеко не всегда, в этом случае на входы С приходится подавать сигнал Т_с, возвращаясь к схеме синхронного счетчика. Скажем, счетчики, работающие в коде ГРЕЯ, реализуются только в синхронном варианте.

После заполнения таблицы 8 производится подбор сигналов, подаваемых на входы С. Обычно в качестве таких сигналов используются сигналы со счетного входа 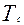, или с прямых, или инверсных выходов триггеров ( 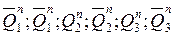). При этом обязательно необходимо учесть специфику работы триггера (например, динамическое управление перепадом). В случае JK триггеров, напомним, разрешающим сигналом на тактирующем входе будет отрицательный перепад ( 1 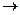0). Именно при таком сигнале триггер получит возможность переключаться, именно такой сигнал у нас закодирован символом «1» в правой части таблицы. Так, первый разряд, тактирующий вход которого подключен к счетному входу счетчика будет иметь возможность переключаться при каждом отрицательном перепаде счетного сигнала.

Произведем подбор сигнала на тактирующем входе второго разряда. Общие требования к сигналу, подаваемому на тактирующие входы следующие:

а) сигнал обязательно должен быть разрешающим, когда триггер меняет свое состояние (там, где С = 1 в табл.8);

б) в остальных тактах (строках) желательно, но не обязательно, чтобы данный сигнал не был разрешающим для триггера (пустые строки в табл.8) , и, если это не удается, то лучшим будет тот сигнал, который создает большее количество нулей (С = 0) в пустых строках столбцов сигналов С. В качестве внутреннего сигнала на тактирующем входе второго разряда, в общем случае могут выступать 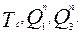Сигнал с выхода второго разряда 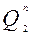использовать нельзя, т.к. триггер не может синхронизировать сам себя!

Проанализируем возможности их использования. Счетный сигнал создает разрешающий перепад 1 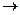0 во всех тактах, в том числе в тех четырех тактах, где он необходим (табл.8), следовательно, сигнал 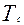вполне может быть использован для управления записью информации во втором триггере. Однако этот сигнал имеет разрешающий перепад и в других тактах, где желательно его не иметь, поскольку при этом триггер будет функционировать как в синхронном счетчике, и никакого упрощения уравнений входов не получится. Попытаемся использовать другие сигналы. Сигнал с выхода третьего разряда использовать нельзя , потому что он имеет за весь цикл работы только один разрешающий перепад 1 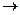0 при переключении счетчика из комбинации 111 в 000, тогда как триггер второго разряда переключается четыре раза.

Наиболее подходящим сигналом, подаваемым на тактирующий вход второго разряда является сигнал с выхода первого разряда 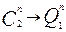, поскольку он, с одной стороны, обеспечивает, когда это необходимо, разрешающий перепад 1 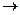0 и не имеет такого во всех (это также удается подобрать далеко не всегда!) остальных случаях. Такой сигнал, создающий максимально возможное число не разрешающих переходов, является лучшим, именно при нем максимально упрощаются уравнения входов.

В случае невыполнения (при возможности, конечно) этого условия, задача синтеза асинхронного счетчика считается нерешенной!

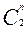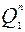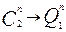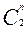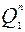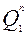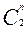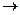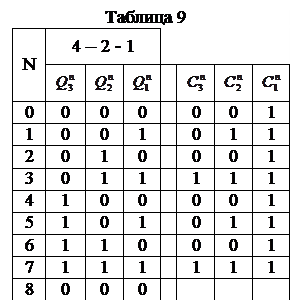
Итак, вход подключаемый к выходу , это условно будем в дальнейшем обозначать . Знак равенства некорректен, поскольку сигналы и в таблице 8 имеет разную кодировку (под = 1 понимается постоянно действующее напряжение, соответствующее логической единице, а под = 1 понимается разрешающий сигнал триггера, в нашем случае переход 1 0). Затем при выбранном сигнале на тактовом входе дозаполняем столбец, отображающий сигнал на входе 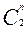, т.е. ставим символ «0» или «1» в пустых строках, как это сделано в таблице 9.

Совершенно аналогично находим сигнал, подаваемый на вход С триггера третьего разряда в качестве этого сигнала, по названным правилам, лучше всего использовать сигнал с выхода второго разряда, поскольку он создает (кроме необходимых единиц) большее количество нулей в пустых строках столбца .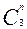

Таким образом, в таблице 9 показаны уже реально действующие сигналы на входах 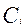, могущие не совпадать с указанными (желаемыми) в табл.8.

Окончательно получаем уравнения входов синхронизации:

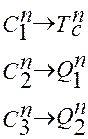( 2.16)

3. Заполняем прикладные диаграммы Вейча по тем же правилам, что и при синтезе синхронных счетчиков, с единственным дополнением, а именно : отмечаем крестиком те ячейки диаграмм, где триггер совершает переход 0 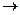0 или 1 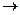1 без разрешающего сигнала на входе С, т.е. отметим ячейки соответствующие комбинациям аргументов 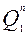; ; 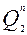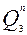,на которых 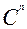= 0 (из табл.0). В прикладной диаграмме 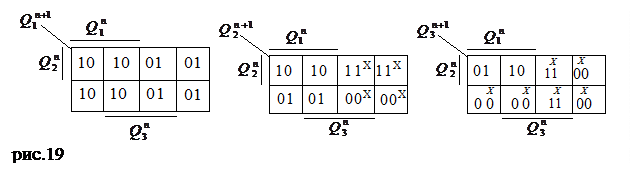Вейча (рис. 19) для первого разряда таких переходов нет. В прикладной диаграмме

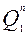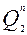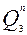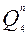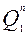
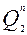
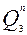
Вейча для второго разряда таких ячеек четыре, например, при = = = =0 (ячейка 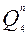) разрешающего сигнала на тактирующем входе 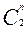нет ( 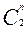= 0 по табл.9). В прикладной диаграмме для третьего разряда ячеек, отражающих переходы 0 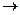0, и 1 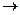1 в отсутствии разрешающего перепада на 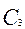- шесть.

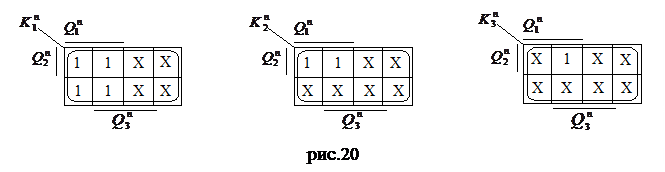4. Заполняем диаграммы Вейча для уравнений входов (рис.20)

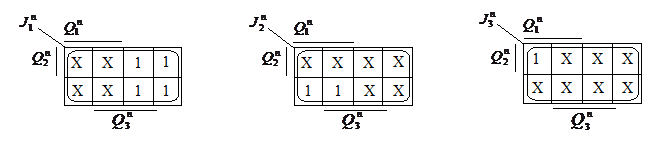аналогично их заполнению при синтезе синхронных счетчиков, за исключением ячеек, отмеченных крестиками. Поскольку эти ячейки, соответствуют переходам 1 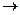1, или 0 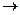0, совершаемым при отсутствии разрешающего сигнала на входе С, то на информационные входы можно подавать любые сигналы. Сравним диаграммы Вейча для уравнений входов асинхронного (рис.20) и синхронного (рис.7) триггеров.

В диаграммах для второго и третьего разряда (рис.20) ячеек, где сигналы могут быть доопределены факультативно (т.е. любым нужным нам образом), существенно больше и, следовательно, уравнения входов асинхронного счетчика получаются существенно проще.

5. Уравнения входов асинхронного счетчика:

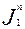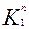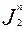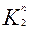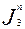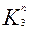= = = = = =1 (2.17)

6. Уравнения входов имеют максимально простой вид, поэтому их перевод в структурную форму производить не надо.

7. По найденным сигналам на тактирующих входах (уравнениям тактирующих входов (2.16)) и по уравнениям информационных входов (2.17) изображаем схему счетчика (рис.21)

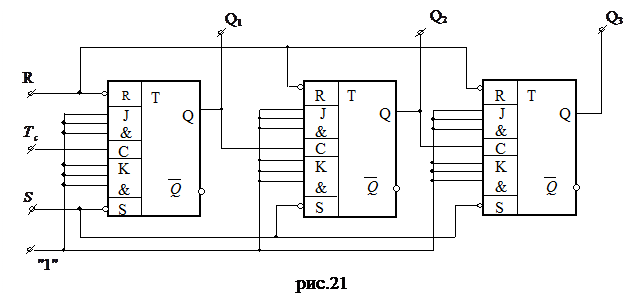Анализ функционирования такого счетчика особенно прост, т.к. каждый разряд переключается из режима хранения в режим инвертирования предыдущего значения выходным сигналом предыдущего разряда (кроме первого). Временные диаграммы приведены на рис.9.