СЧЕТЧИКОВ
Реверсивные асинхронные счетчики также могут быть построены двух видов: с одним счетным входом и одним входом управления; либо с двумя счетными входами. Мы будем рассматривать первый вариант, ограничиваясь, для простоты, четырехразрядными счетчиками. Сравнивая методики синтеза синхронных (п.2.2) и асинхронных (п.2.7) счетчиков, можно заметить, что они отличаются лишь составлением уравнений тактирующих входов и упрощения, за счет появления безразличных состояний в диаграммах Вейча, уравнений входов информационных. Следовательно, можно предположить, что синтез реверсивных асинхронных счетчиков будет отличаться от соответствующего синхронного аналога, лишь фактом объединения уравнений для тактирующих входов (в зависимости от сигнала управления Р) суммирующего и вычитающего асинхронных счетчиков.
Таким образом, последовательность синтеза произвольного асинхронного реверсивного счетчика должна быть следующая:
1. Условимся считать, что счетчик переходит в суммирующий режим при Р = 1, а в режим вычитания при Р = 0.
2. В соответствии с методикой п.2.7 получаем уравнения тактирующих (2.20) и информационных (2.21) входов для суммирующего (Р = 1) и вычитающего (Р = 0) счетчиков, на одном и том же типе триггеров, с одинаковым числом разрядов, и коде в котором они работают.
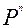 =1
=1 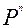 = 0
= 0
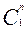 =
= 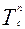
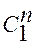 =
= 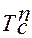
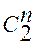 =
= 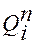 ,
, 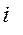 = 1¸4;
= 1¸4; 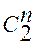 =
= 
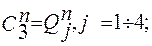
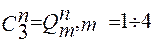 (2.20)
(2.20)
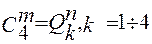 ;
; 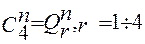
где 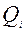 -
- 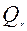 - выходы триггеров (i ¸ r) – го разрядов в прямой или инверсной форме и при использовании, например, JK триггеров:
- выходы триггеров (i ¸ r) – го разрядов в прямой или инверсной форме и при использовании, например, JK триггеров:
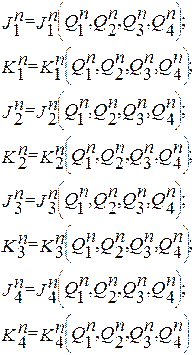
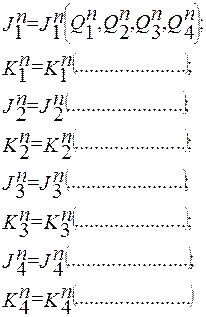 (2.21)
(2.21)
1. Уравнения тактирующих входов реверсивного асинхронного счетчика находят по правилам, изложенным в п.2.5. (выражений 2.10 – 2.13), полагая, что теперь 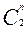 является функцией уже не одного а трех аргументов, т.е.
является функцией уже не одного а трех аргументов, т.е.
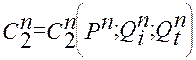 (2.22)
(2.22)
Далее строят таблицу, аналогично табл. 5, 6 где, перебирая все 8 возможных комбинаций переменных 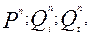 каждой из них ставится в соответствие значение
каждой из них ставится в соответствие значение 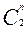 , исходя из выражений 2.20 (табл.10).
, исходя из выражений 2.20 (табл.10).
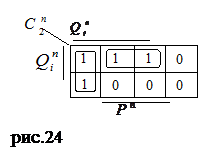
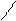
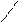





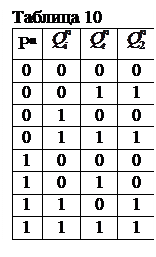 Перенося полученные значения на диаграмму Вейча (рис.24) для уравнения тактирующих входов первого разряда считываем с нее минимизированное выражение для функции
Перенося полученные значения на диаграмму Вейча (рис.24) для уравнения тактирующих входов первого разряда считываем с нее минимизированное выражение для функции 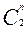 min:
min:
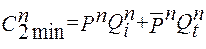 (2.23)
(2.23)
В тех случаях, когда требуется использовать элементы многоступенчатой логики типа К155ЛР1, ЛР3, ЛР4 и т.д. Считывание (минимизацию) с диаграмм Вейча удобно производить «по нулям» (п.2.6 «ПРИЛОЖЕНИЯ»). В этом случае получаем:
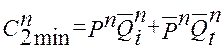 (2.24)
(2.24)
2. Получаем аналогичные уравнения для третьего и четвертого разрядов.
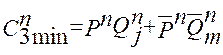 (2.25)
(2.25)
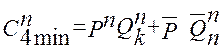 (2.26)
(2.26)
3. Уравнения входов реверсивного асинхронного счетчика, получают из (2.21) по аналогии с п.2.5.
4. По получении уравнениям тактирующих и информационных входов изображаем схему счетчика.
Рассмотренной методикой можно пользоваться при произвольном числе разрядов счетчика, а п.2.-4 также в тех случаях, когда, например, при 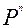 =1 ,
=1 , 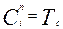 , а при
, а при 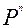 = 0,
= 0, 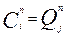 . В этом случае выражение (2.22) приобретает вид:
. В этом случае выражение (2.22) приобретает вид:
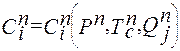 (2.27)
(2.27)
т.е. сигнал 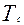 - можно считать обычным аргументом функции
- можно считать обычным аргументом функции 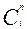 .
.
Дата добавления: 2014-12-20; просмотров: 1048;
