Классификация счетчиков по основанию системы счисления

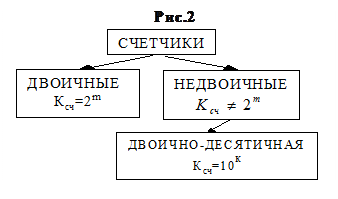Критерием, по которому различаются счетчики, является модуль счета. Двоичный счетчик ( 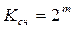) считает всевозможные числа, которые могут быть представлены m - разрядным двоичным натуральным кодом «8 – 4 – 2 – 1».

Недвоичные счетчики используют несколько меньшее число кодовых комбинаций, за счет чего появляются состояния, количество которых L определяется выражением

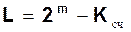,где(2.2)

m – количество разрядов счетчика

К_сч – его модуль счета

В особую группу на практике выделяют двоично-десятичные счетчики, имеющие К_сч = 10, 100, 1000 и т.д.

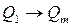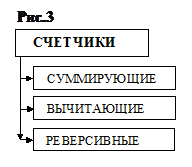
Каждой кодовой комбинации на выходах счетчика ставится в соответствие некоторое число N, отражающее количество подсчитанных импульсов. При поступлении на вход счетчика очередного (N + 1) счетного импульса меняется его состояние, т.е. кодовая комбинация 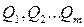, или число, записанное в счетчик. Это число может быть меньше или больше предыдущего. Данное обстоятельство позволяет произвести классификацию счетчиков (рис.3)

Классификация счетчиков по направлению изменения состояний

В суммирующих счетчиках показания увеличиваются при поступлении счетных импульсов, т.е. осуществляется их суммирование. В вычитающих счетчиках показания уменьшаются, т.е. происходит вычитание из числа, записанного в счетчике (а в исходном состоянии, это, как правило, максимальное число, соответствующее кодовой комбинации 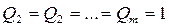) каждого поступающего счетного сигнала. Реверсивные счетчики могут работать как в режиме суммирования, так и в режиме вычитания, в зависимости от внешнего сигнала управления.

Классификация счетчиков по способу

переключения разрядов

Если при поступлении счетного импульса триггеры всех разрядов счетчика переключаются одновременно (или параллельно), то такой счетчик является счетчиком с асинхронным способом переключения разрядов, или просто синхронным счетчиком (рис.4).

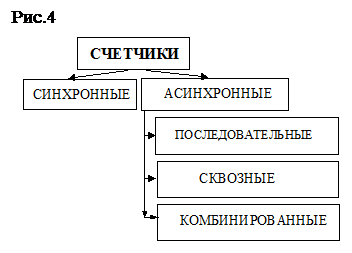Счетчики, у которых триггеры переключаются не одновременно, называются асинхронными. Асинхронные счетчики в свою очередь могут быть последовательными, т.е. такими, у которых триггер последующего разряда переключается сигналом с предыдущего.

В асинхронных счетчиках со сквозным способом переключения счетный сигнал поступает на триггеры через некоторую цепочку логических элементов. Счетчики с комбинированным способом переключения разрядов сочетают в себе какие – либо перечисленные способы, например, группы разрядов переключаются синхронно, а между собой связаны последовательно и т.д.

Показания счетчика (комбинации 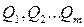) могут быть представлены различными кодами, т.е. соответствием комбинации на выходах и числа записанного в счетчике. Могут быть синтезированы счетчики, работающие как в двоичном, например ''8-4-2-1'', ''5-2-1-1'', так и недвоичных кодах, например, Грея, Джонсона, ''1 из m''. Рассматриваемые ниже методы синтеза счетчиков позволяют проектировать синхронные и асинхронные счетчики, работающие в любом коде.

2.2. МЕТОДИКА СИНТЕЗА СИНХРОННЫХ СЧЕТЧИКОВ

Рассмотрение метода синтеза счетчиков начнем со способов логического проектирования наиболее быстродействующих (с минимальным Т_сч) синхронных счетчиков.

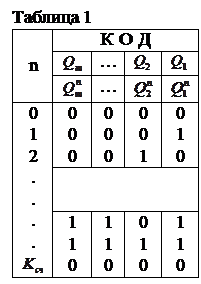
Отправной информацией при синтезе будем считать таблицу функционирования (табл.1), в которой отражены состояния всех разрядов счетчика 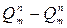при последовательном поступлении на его счетный вход импульса в каждом n - ом такте работы.

Такая таблица может быть составлена, если известны модуль счета – К_сч счетчика и код, в котором работает счетчик, следующим образом. В каждом такте кодовая комбинация записывает по аналогии с выражением (2.2) «ПРИЛОЖЕНИЯ», путем представления десятичного числа n (номера такта) его кодом. 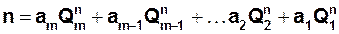(2.3)

Требуемое число разрядов счетчика необходимо для возможности подсчета

К_сч импульсов определяется выражением 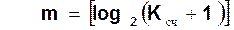(2.4):

(2.4)

где [ ] - означают округление до ближайшего целого числа.

Примечание: формулой 2.4 можно пользоваться только для двоичных кодов.

Для реализации синхронного (параллельного или одновременного) способа переключения разрядов необходимо счетный сигнал подать на входы синхронизации С триггеров всех m разрядов. Тип триггеров, с помощью которых синтезируется счетчик, выбирается исходя из имеющегося их набора в используемой серии микросхем, быстродействия, простоты схемы и т.д. Таким образом, фактически до начала собственного синтеза синхронного счетчика мы имеем его таблицу функционирования и незавершенную схему (рис.5).

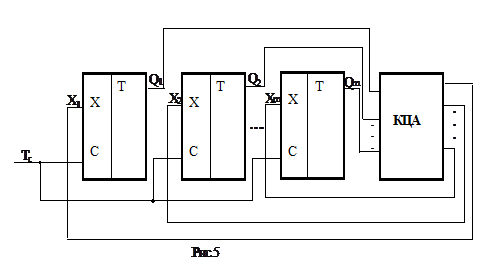Схема счетчика содержит m синхронных триггеров , тактовые входы С которых соединены со счетным входом счетчика, а выходы триггеров являются выходами счетчика. Чтобы не нарушать общности рассуждений, на схеме изображен произвольный триггер с информационным входом (или выходом) Х, в качестве которого может быть, например вход D (у D триггера), входы J и K у универсального JK триггера.

Основная часть проектирования счетчика или собственно синтез состоит в определении сигналов, которые надо подать на информационные входы триггеров всех разрядов 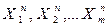для того, чтобы каждый из них переключался в соответствии с таблицей функционирования (табл.1), т.е. определении логических функций вида:

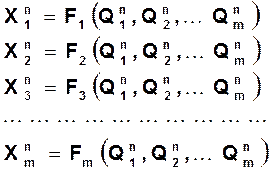
(2.5)

называемых у р а в н е н и я м и в х о д о в триггеров. По этим выражениям строится КЦА – комбинационный цифровой автомат, т.е. завершается синтез счетчика. Физически КЦА осуществляет связь источников сигналов, а это могут быть только выходы триггеров – прямой или инверсный, с нагрузками – информационными входами триггеров, причем в каждом такте эти связи могут быть разными.

Уравнения входов находятся следующим образом. Из заданной таблицы функционирования счетчика можно составить систему уравнений (2.6), заданных таблично, в виде диаграмм Вейча.

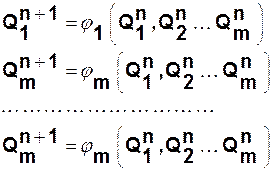(2.6)

называемых п р и к л а д н ы м и у р а в н е н и я м и , поскольку каждая следующая ( n+1) строчка в таблице функционирования показывает чему будет равно 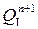(для всех m разрядов), если предыдущее n-ое состояние (предыдущая n - ая строка) описывалось набором .

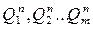Подчеркнем, что прикладные уравнения (2.6) показывают, как должен переключатся каждый триггер с тем, чтобы реализовать заданную таблицу функционирования.

Кроме прикладных уравнений нам известны таблицы переходов (табл.2)

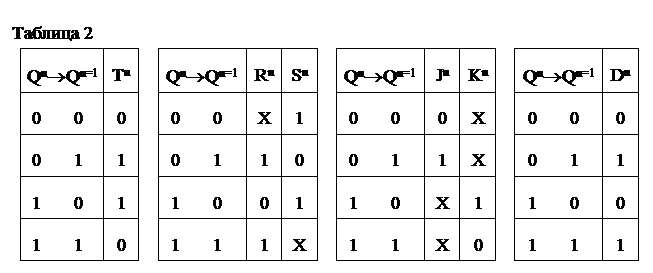
Различных типов триггеров (для RS триггера приведена его разновидность с инверсными входами), показывающих какие сигналы надо подать на информационные входы в n- ом такте, чтобы, при наличии разрешающего сигнала на входе синхронизации, триггер совершил требуемый нам переход: 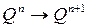(из таблицы функционирования). Знаком Х обозначены безразличные состояния переменной, что физически соответствует возможности подачи произвольного сигнала на вход для совершения соответствующего перехода.

Решая каждое из прикладных уравнений (2.6) совместно с таблицей переходов (табл.2) относительно Хⁿ ,можно решить уравнения входов. Это можно делать разными способами, но главное – получить наиболее простые уравнения входов, что обеспечит простую схемную реализацию устройства.

Воспользуемся с помощью диаграмм Вейча табличным методом нахождения уравнения входов, который позволит достаточно просто их определить в минимизированном виде. Этот метод проиллюстрируем на примере синтеза различных счетчиков.

Таким образом, окончательно можно сформулировать последовательность синтеза синхронных счетчиков. Синтез синхронных счетчиков при заданном модуле счета К_сч и коде (обычно дополнительно задается видом счетчика – суммирующей или вычитающей и типом используемых триггеров) в котором работает счетчик производится в шесть этапов:

1. Определение количества разрядов (по выражению 2.4) и составление таблицы функционирования.

2. Заполнение прикладных диаграмм Вейча.

3. Заполнение диаграмм Вейча для уравнений входов с использованием прикладных диаграмм Вейча и таблиц переходов используемых триггеров.

4. Считывание с диаграмм Вейча уравнений входов в минимизированном виде.

5. Перевод уравнений входов в структурный вид в используемом базисе логических элементов.

6. Изображение схемы счетчика (в соответствии с рис.5)