На JK триггерах.

I. Количество разрядов (триггеров) определяем по 2.4

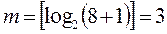
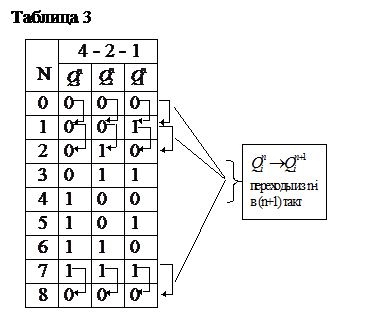Таблица функционирования заполняется с учетом кода, в котором работает счетчик, таким образом, чтобы при подаче счетных импульсов в счетчике последовательно фиксировались все числа от 0 до 7. Так комбинации 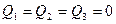соответствует число 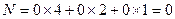; комбинации 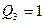; ; 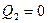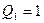,соответствует число 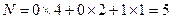.После того, как счетчик исчерпает все свои К_сч=8 состояний, он возвращается в исходное состояние. Таким образом, получаем таблицу 3.

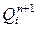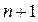Прикладные диаграммы Вейча отображают уравнения (2.6) и заполняют для каждого разряда по таблице функционирования счетчика. Функциями этих диаграмм являются (в ( ) такте), а аргументами 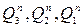(в n-такте).

Заполнение прикладных диаграмм ведется по следующим правилам:

а) Отыскиваем ячейку диаграммы Вейча для первого разряда- 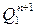,соответствующую N=0,коомбинации 000,или минтерму 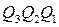(в правом нижнем углу, по правилам, изложенным на рис.6 ''ПРИЛОЖЕНИЯ'').

б) В эту ячейку заносятся две цифры: левая отражает состояние триггера на данном наборе в n-ом такте (в нашем случае 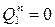), правая - в такте (n+1) (в нашем случае 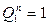), соответствующих переходам показанным вертикальными стрелками в табл.3.

в) Повторяем п. а), б) для ячейки соответствующей N=1,2…7.

г) Повторяем п. а), б), в) для второго и третьего разрядов.

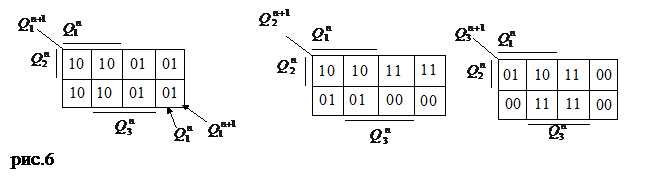Полученные диаграммы представлены на рис.6

3.При заполнении диаграмм Вейча для уравнений входов воспользуемся таблицей переходов триггера, используемого для построения счетчика. Рассматриваемый метод синтеза позволяет проектировать счетчики на любом типе триггеров, однако для каждого типа триггера будут свои уравнения входов и свои особенности функционирования.

Рассмотрим синтез на универсальных JK триггерах.

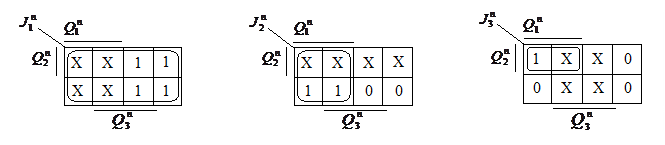
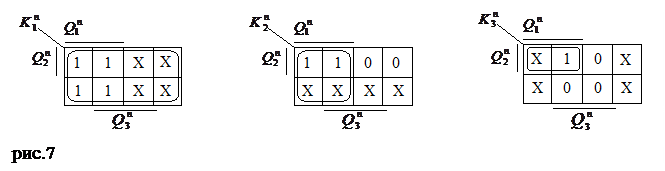Поскольку каждый из трех, используемых для построения счетчика JK триггеров имеет по два информационных входа J и K,необходимо иметь по две диаграммы Вейча на каждый разряд. Аргументы этих диаграмм (рис.7)

Целесообразно располагать в том же порядке, что и на прикладных диаграммах (рис.6).В этом случае заполнение диаграмм Вейча для уравнений входов производится весьма просто. Например, триггер первого разряда при сигнале

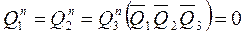переключается из состояния 0 в состояние 1,т.е. совершает переход 0→1.Из таблицы переходов JK триггера (табл.2) видно, что такой переход, совершается при J=1,K=0 или 1 (что условно обозначено X).Значит, в данную ячейку диаграммы Вейча для уравнений входов необходимо внести единицу для уравнений J и ''X'' означающий произвольный сигнал для уравнений K. Аналогично заполняются все остальные ячейки диаграмм Вейча для уравнений входов всех разрядов.

4.Считывание уравнений входов в минимизированном виде производится по правилам, изложенным в п.2.5, 2.6 ''ПРИЛОЖЕНИЯ''. Вариант до определения и объединения единиц в контуры, представлен на рис.7. В результате получаем уравнение входов:

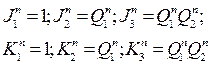(2.7)

5.Для построения схемы, отметим, что уравнение входов (2.7),реализуются с помощью КЦА, которые могут строиться на различных логических элементах. В этом случае уравнения (2.7) необходимо привести в структурный вид, соответствующий требуемому базису, пользуясь правилами и тождествами булевой алгебры. Однако в данном случае, в такой необходимости нет, поскольку у JK триггеров информационные входы по J и по K конъюнктивно связаны, т.е. для сигналов на них подаваемых выполняется операция ''ЗИ'', что отражено знаком &. Следовательно, для реализации уравнений (2.7) внешних элементов не требуется.

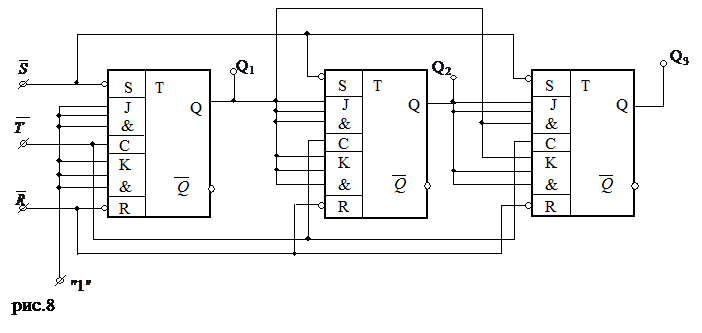
6.Схема синхронного двоичного счетчика, построенная по уравнениям 2.7, приведена на рис.8.

Уравнение входов первого разряда имеют максимально простой вид, поэтому для их реализации достаточно подключить все входы J и K к генератору единицы. Входы J и K второго разряда могут быть подключены двумя способами: соединением всех входов с выходом триггера первого разряда (рис.8) или соединением одного входа J и одного входа K с выходом Q₁ первого разряда и подключением всех оставшихся входов к генератору единицы. Аналогично производится соединение информационных входов триггера третьего разряда. Входы S и R предназначены для синхронной установки перед подачей сигнала Т_с всех триггеров в единицу и 0 соответственно путем подачи на них уровня логического нуля.

Проведем анализ функционирования синтезированного счетчика, для чего построим временные диаграммы сигналов на его счетном входе и всех выходах (рис.9).

Пусть на вход Т_с постоянно поступают счетные прямоугольные импульсы с частотой f_вх. Будем считать, что перед поступлением первого импульса в момент времени t₀ счетчик был обнулен, т.е. .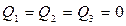

Поскольку JK триггера переключаются по отрицательному перепаду на входе C для построения временных диаграмм необходимо определить по схеме какие сигналы окажутся на входах J и K каждого разряда к моменту прихода отрицательных перепадов (на рис.9 это t₁-t₁₀).

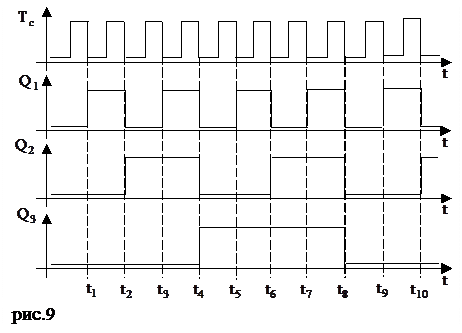Первый разряд Q₁ по каждому перепаду будет инвертировать предыдущее значение, т.к. постоянно .

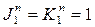Второй разряд Q₂ в моменты t₁,t₃,t_5,t₇,t₉ будет инвертировать предыдущее значение, т.к. несмотря на наличие разрешающего перепада на входе, 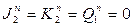. В моменты t₂,t₄,t₆,t₈,t₁₀ – осуществляет инверсию предыдущего состояния, т.к. 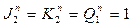(статические).

Третий разряд Q₃ в моменты времени t₁-t₃ осуществляет хранение информации, т.к. несмотря на наличие разрешающих перепадов 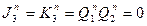(т.к. хотя бы одно из значений, либо Q₁ либо Q₂, либо оба вместе равняются нулю). И лишь в моменты совпадения двух факторов: наличия разрешающего перепада и 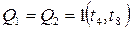триггер Q₃ будет инвертировать свое состояние (т.е. переключаться).

Из временных диаграмм видного сигнала Т_с на два, на четыре, на восемь. В общем случае для любого m-разрядного счетчика, работающего в произвольном двоичном коде частота сигнала f_вых на выходе старшего m-го разряда делится в К_сч раз: 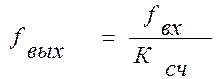(2.7)

Таким образом, такие счетчики могут использоваться в качестве делителей частоты.