Построение эпюр нормальных сил N
Правило знаков для N имеет физический смысл: нормальная сила является положительной, если вызывает растяжение бруса, отрицательной – если сжатие.
Пример 1 (рис. 1.3).
Если на стержень действуют силы, приложенные вдоль его оси, то он находится в условиях растяжения и остается только один внутренний фактор N.
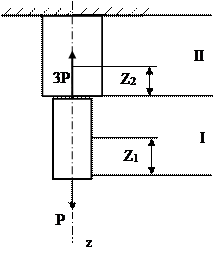 |
Рис. 1.3 Стержень
Порядок построения эпюр:
1. Определяем реакции опор.
2. Разбиваем стержень на участки.
Участок – часть стержня между точками приложения сосредоточенных сил, включая опорные реакции.
3. Записываем аналитические выражения для внутренних силовых факторов.
4. Строим график (эпюру) (рис. 1.4).
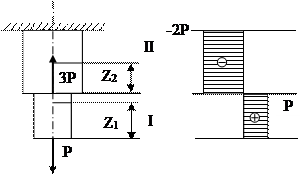
Рис. 1.4 Построение эпюры нормальных сил
Эпюра – график, заштрихованный линиями, перпендикулярными оси.
Используя метод РОЗУ, отбрасывают ту часть, где больше нагрузки.
Внутренний фактор – равнодействующая внутренних сил.
Nz2 = P-3P = -2P
Nz2 = P-3P = -2P
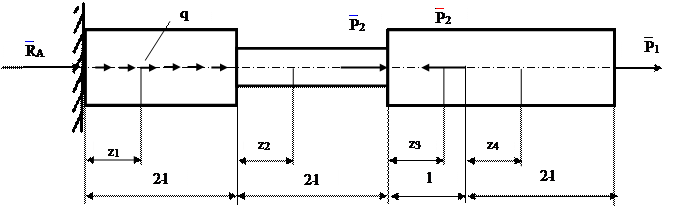
Пример 2 (рис. 1.5).
Построить эпюру нормальных сил N.
q – интенсивность равномерно – распределенной нагрузки.
Опасное сечение в заделке, т.к. там самое большое значение N.
 | |||||
 | |||||
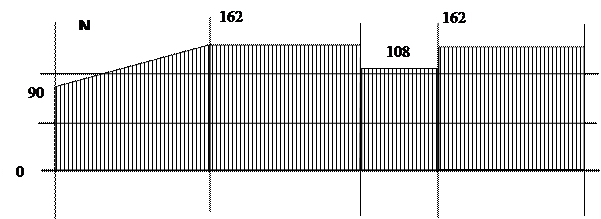 |
Рис. 1.5 Построение эпюры нормальных сил
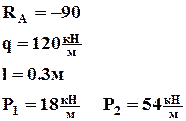
Построим эпюру нормальных сил
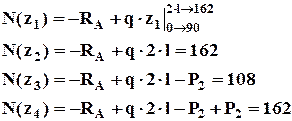
1.2 Построение эпюр крутящих моментов
Под кручением понимается такой вид нагружения, при котором в поперечных сечениях стержня возникает только крутящий момент, а прочие силовые факторы равны нулю. Для крутящего момента, независимо от формы сечения, принято следующее правило знаков.
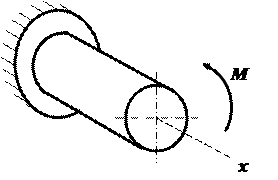 |
Рис. 1.6 Правило знаков для крутящего момента
Если со стороны внешней нормали к сечению вращение осуществляется против часовой стрелки, то крутящий момент положительный (рис.1.6).
Правило знаков носит формальный характер (можно установить произвольно).
 Стержень, в основном работающий на кручение, называется валом.
Стержень, в основном работающий на кручение, называется валом.
Рис.1.7 Схематичное изображение крутящего момента (против часовой стрелки).
Пример(К - 1)
Построить эпюру крутящих моментов (рис 1.9).
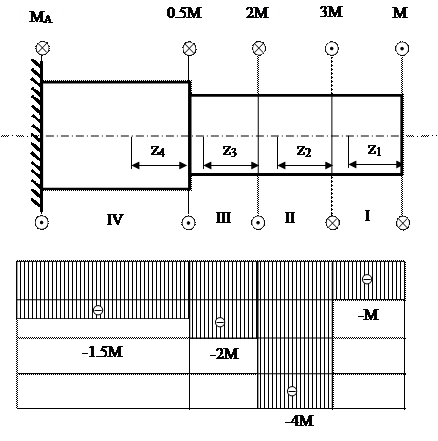 |
Рис.1.9 Построение эпюры крутящих моментов

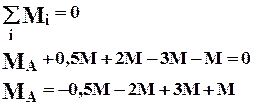
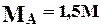
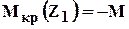
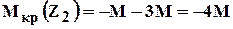
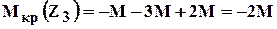
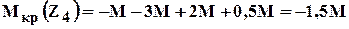
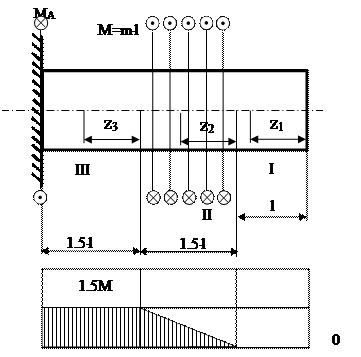 Пример на построение эпюры крутящих моментов (рис 1.10).
Пример на построение эпюры крутящих моментов (рис 1.10).
Рис.1.10 Построение эпюры крутящих моментов
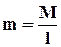
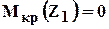
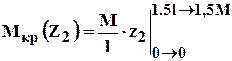
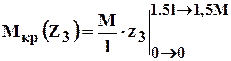
1.3 Построение эпюр поперечных сил Q и изгибающих моментов M для балок
Балка – стержень, в основном работающий на изгиб. При расчете балку принято заменять ее осью, все нагрузки приводятся к этой оси, а силовая плоскость будет совпадать с плоскостью чертежа.
Вал – стержень в основном работающий на кручение.
Виды опор:
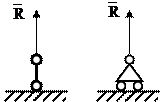 Шарнирно-подвижная опора – опора, в которой может возникать только одна составляющая реакции, направленная вдоль опорного стержня (рис.1.11).
Шарнирно-подвижная опора – опора, в которой может возникать только одна составляющая реакции, направленная вдоль опорного стержня (рис.1.11).
Рис.1.11 Шарнирно-подвижная опора
Шарнирно-неподвижная опора –опора, в которой могут возникать две составляющие реакции: вертикальная и горизонтальная (рис.1.12).
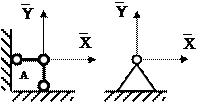 |
Рис.1.12 Шарнирно-неподвижная опора
Заделка(жесткое защемление) – опора, в которой могут быть: вертикальная и горизонтальная реакции и опорный момент (рис.1.13).
 |
Рис.1.13 Заделка
|
|
|
|








|
|

|
|





|
|




 1.3.1 Правило знаков для Q
1.3.1 Правило знаков для Q
 |
1.3.2 Правило знаков для М
Эпюру для М строят на сжатых волокнах.
 | |||
 |
Пример (Э-3)
Построить эпюры внутренних усилий Q и M для однопролетной балки (рис. 1.14).
 |
Рис. 1.14 Расчетная схема
Дано:
Р=0,5qa
M=0,5qa2
Решение:
Вычислим реакции опор.
Освободим балку от связей и заменим их действие реакциями.
Y: RA-P-q·2a+RB=0
Составим уравнения равновесия:
Сумма моментов всех сил относительно точки А равна
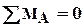
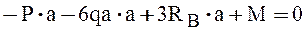
откуда
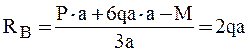
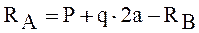
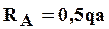
Сумма моментов всех сил относительно точки В равна
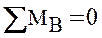
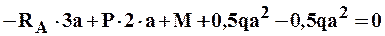
Разделим балку на четыре участка. Применим метод сечений на каждом из участков и запишем выражения для внутренних усилий
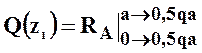
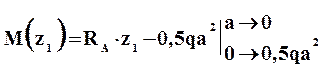
Внутренние усилия на втором участке равны
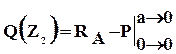
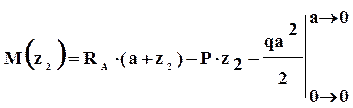
На третьем участке
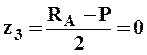
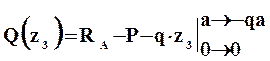
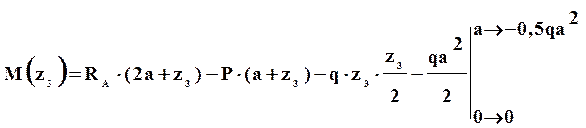
Внутренние усилия на четвертом участке равны
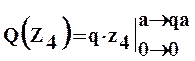
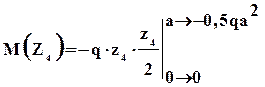
Строим эпюры для M и Q (рис 1.15). Для проверки правильности полученных эпюр могут быть использованы следствия из дифференциальных зависимостей между Q и M.
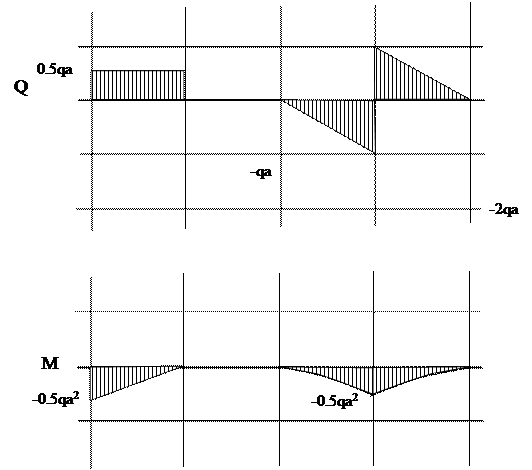
Рис. 1.15 Построение эпюр Q и M
2. Дифференциальные зависимости при изгибе
Пусть стержень закреплен произвольным образом и нагружен распределенной нагрузкой q=f(z), принятое направление q считать положительным (рис. 2.1).
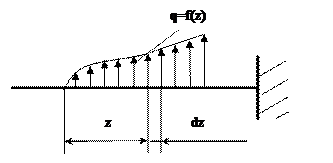
Рис. 2.1 Стержень с распределенной нагрузкой
Выделим из стержня элемент длиной dz и в проведенных сечениях приложим моменты M и M+dM, а также поперечные силы Q и Q+dQ (рис. 2.2). В пределах малого отрезка dz нагрузку q можно считать равномерно распределенной.
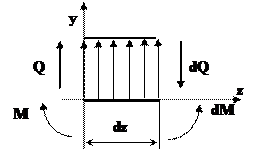
Рис. 2.2 Элемент длиной dz стержня
Приравниваем нулю сумму проекций всех сил на вертикальную ось y и сумму моментов относительно поперечной оси:
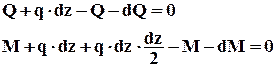
После упрощения получим
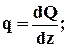
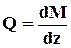
Из полученных соотношений можно сделать некоторые общие выводы о характере эпюр изгибающих моментов и поперечных сил для прямого стержня.
2.1 Правила проверки эпюр
1. Если на участке отсутствует распределенная нагрузка, то есть q = 0, 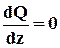 =>Q=const=C1;
=>Q=const=C1; 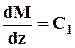 => M=C1×z+D1,то эпюра поперечных сил постоянна, а эпюра изгибающих моментов М изменяется по линейному закону (рис. 2.3).
=> M=C1×z+D1,то эпюра поперечных сил постоянна, а эпюра изгибающих моментов М изменяется по линейному закону (рис. 2.3).
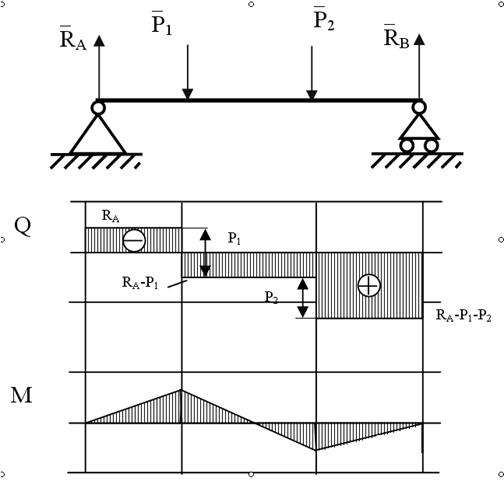
Рис. 2.3 Эпюра поперечных сил и изгибающих моментов
2. Если в сечении приложена сосредоточенная сила, то на эпюре Q скачек на величину этой силы, от начала предыдущего, до начала следующего. А на эпюре М излом, направленный навстречу этой силе.
3. Если первая производная положительная, то момент возрастает слева направо, если отрицательная, то наоборот: +Q => M -Q => M¯.
4.  Если в сечении приложен сосредоточенный момент Мi, то на эпюре Q нет никаких изменений, а на эпюре М скачек на величину этого момента (рис. 2.4).
Если в сечении приложен сосредоточенный момент Мi, то на эпюре Q нет никаких изменений, а на эпюре М скачек на величину этого момента (рис. 2.4).
Рис. 2.4 Эпюра поперечных сил и изгибающих моментов
5. 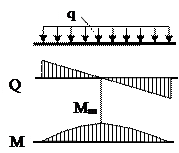 Если на участке приложена равномерно распределенная нагрузка q = const, то Q – наклонная прямая, а М – парабола, выпуклость которой направлена навстречу нагрузке (рис. 2.5).
Если на участке приложена равномерно распределенная нагрузка q = const, то Q – наклонная прямая, а М – парабола, выпуклость которой направлена навстречу нагрузке (рис. 2.5).
Рис. 2.5 Эпюра поперечных сил и изгибающих моментов
6. Если на участке эпюра Q меняет знак и пересекает ось, то эпюра М имеет экстремум в точке пересечения Q с осью.
7. Если ветви эпюры Q сопрягаются без скачка на границах участка, то ветви эпюры М на границе этих же участков сопрягаются без изломов (рис. 2.6).
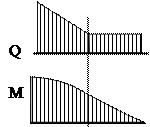
Рис. 2.6 Эпюра поперечных сил и изгибающих моментов
8. Если на участке стержня Q равна нулю, то 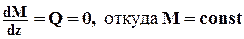 (рис. 2.7)
(рис. 2.7)

Рис. 2.7 Эпюра поперечных сил и изгибающих моментов
3. Напряжения и деформации
|
 | |||
|
Рис. 3.1 Поперечное сечение бруса
Введем понятие касательного и нормального напряжений:
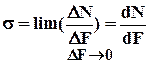 нормальное напряжение
нормальное напряжение
Нормальное напряжение – это предел отношения нормальной составляющей внутренних усилий DN, действующих на элементарную площадку DF при стремлении последней к нулю.

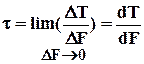 касательное напряжение
касательное напряжение
Касательное напряжение – это предел отношения тангенциальной составляющей внутренних усилий DT, действующих на элементарную площадку DF при стремлении последней к нулю.
Общий вид формул:
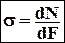
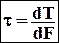
Закон парности касательных напряжений 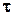
«Вырежем» элементарную площадку dF бруса размером dx на dy (рис. 3.2).
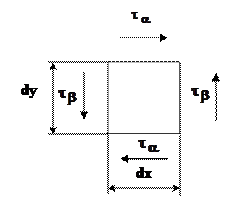
Рис. 3.2 Площадка dF
На двух взаимно перпендикулярных площадках, имеющих общее ребро, касательные напряжения 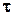 равны по величине и направлены или оба к ребру или оба от ребра.
равны по величине и направлены или оба к ребру или оба от ребра.
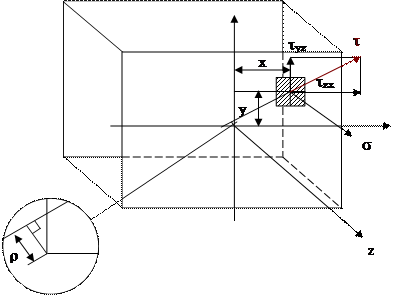
3.1 Интегральные зависимости между s и t и внутренними силовыми факторами
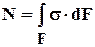
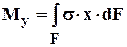
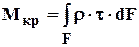
|
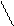

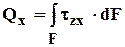
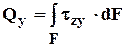
Рис. 3.3Связь между напряжениями и внутренними усилиями
4. Деформации
Ни один из существующих в природе материалов не является абсолютно твердым; под действием внешних сил все тела в той или иной мере меняют свою форму(деформируются).
Изменение формы напряженного тела существенно влияет на распределение в нем внутренних сил, хотя само по себе это изменение формы является, как правило, незначительным и обнаруживается в большинстве случаев только при помощи чувствительных приборов.
Рассмотрим основные виды деформации, которые учитываются при решении задач в сопротивлении материалов.
Дата добавления: 2014-12-20; просмотров: 3536;
