Физическая сторона задачи

Заключается в применении закона Гука.

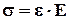(4) где e - относительная деформация,

Е – модуль упругости 1 рода = 2×10⁵ МПа

Объединяем все три стороны задачи

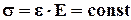(5)

подставляем в интеграл (2)

=>

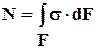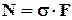
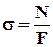(6) s - нормальное напряжение

Найдем растяжение стержня при удлинении, сжатии.

Рис. 6.3 Нормальное напряжение при растяжении

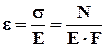E×F – жесткость бруса при растяжении, сжатии.

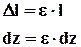
Абсолютная деформация бруса длинной l=e×dz равна

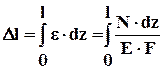где Dl – абсолютная деформация.

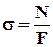
Условия прочности:

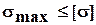
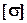- допускаемое нормальное напряжение.

Материалы

Пластичные материалы	Хрупкие материалы
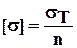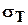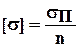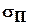- предел текучести материала	- предел прочности материала
n – коэффициент запаса прочности

n – вводится по следующим причинам:

· неточное определение внешних нагрузок

· приближенные методы расчета

· отклонения в размерах деталей

· разброс в механических характеристиках материала.

Для хрупких материалов n больше чем для пластичных материалов, так как у хрупких материалов большая неоднородность структуры.

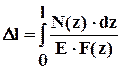
если N(z) = const, F(z) = const

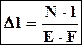
Условие жесткости Dl £ [Dl]

7. Типы задач сопротивления материалов

Мы выполняем расчет по допускаемым напряжениям, при этом вся конструкция считается прочной, если напряжение в опасной точке s_max не превосходит [s] – допускаемого значения (рис. 7.1).

	s

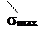Рис. 7.1 Эпюра напряженийs