Процес феодалізації селян і земельні відносини 2 страница

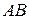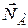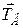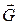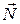Розв’язання. Стержень є невільним тілом. Відкинемо в’язі і замінимо їх дію на стержень силами реакцій: – тиск з боку площини і – натяг нитки. Звільнивши стержень від нитки (після її перепалювання), розглянемо його рух під дією лише двох сил і відносно системи координат Оху. Тут точка О співпадає з початковим положеннім т.А

Покажемо штриховою лінією положення стержня в поточний момент часу і запишемо диференціальні рівняння плоскопаралельного руху цього стержня

; ;

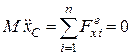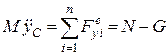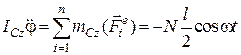. (30.12)

Інтегруємо двічі перше з рівнянь (30.19):

; .

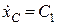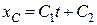Сформулюємо початкові умови:

при 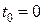маємо ; ,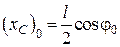

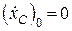тоді

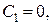
тобто

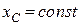Отже, центр мас по відношенню до осі 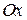знаходиться в стані спокою, тобто центр мас пересувається лише вздовж вертикалі. Такий результат може бути отриманий з третього наслідку теореми про рух центра мас.

В двох останніх рівняннях (30.12) є три невідомі величини 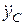, 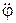і N. Тому для їхнього визначення треба скласти ще одне рівняння, що випливає з обмежень, які накладаються в’язями на рух стержня, тобто

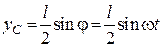Це рівняння є законом руху центра мас стержня вздовж вертикалі. З нього маємо відповідно закони зміни швидкості та прискорення центра мас:

; .

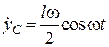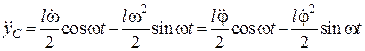Підставляючи отримане значення 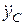до другого рівняння системи (30.12), матимемо:

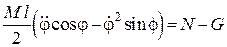. (30.13)

Підставивши значення 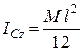до третього рівняння системи (30.12), дістанемо

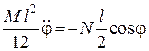
або

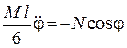. (30.14)

Домножимо рівняння (30.14) на 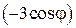і додамо його до рівняння (30.13). Після взаємного знищення деяких доданків, отримаємо:

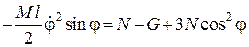звідки

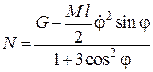У нашому випадку при 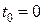: 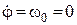; 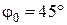реакція площини в точці в момент початку падіння стержня має таке значення:

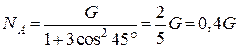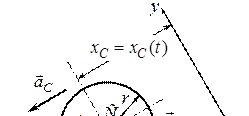Приклад 2. Однорідний циліндр з горизонтальною віссю скочується під дією власної ваги з похилої шорсткої площини. Коефіцієнт тертя ковзання 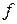. Визначити прискорення осі циліндра, а також знайти кут нахилу 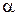площини до горизонту, при якому циліндр котитиметься без ковзання (рис. 30.6).

Розв’язання. Система диференціальних рівнянь плоскопаралельного руху циліндра має вигляд:

;

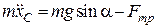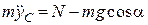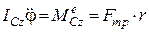. (30.15)

Оскільки циліндр котиться без ковзання, то точка Р – миттєвий центр швидкості 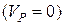. Тому

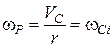а значить

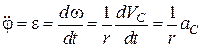З третього рівняння системи (30.15) знаходимо :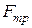

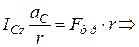
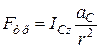З другого рівняння системи (30.15) при 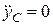знаходимо, що .

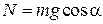З першого рівняння системи (30.15) знаходимо 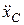:, що дорівнює :

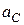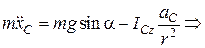
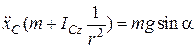звідки

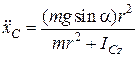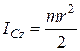, ; або .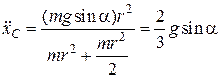

Для того, щоб рух відбувався без ковзання потрібно щоб сила тертя 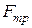при коченні була меншою, ніж сила тертя в момент початку руху.

Остаточно:

; ;

; ,

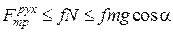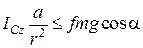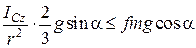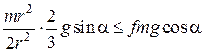звідки

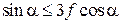, тобто 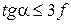і .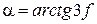

Розділ ХV . ПРИНЦИП ГЕРМАНА - ЕЙЛЕРА - Д’АЛАМБЕРА

Лекція 31

ПРИНЦИП Д’АЛАМБЕРА.

ГОЛОВНИЙ ВЕКТОР І ГОЛОВНИЙ МОМЕНТ СИЛ ІНЕРЦІЇ

31.1. Принцип Д’Аламбера для матеріальної точки

Розглянемо рух невільної матеріальної точки під дією заданих сил. Векторне рівняння руху цієї точки з урахуванням реакцій в’язей має вигляд:

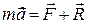Тут 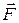– рівнодійна заданих сил, 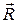– рівнодійна реакцій в’язей.

Якщо 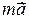перенести в праву частину рівності, то матимемо:

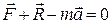. (31.1)

Введемо таке позначення : 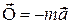. (31.2)

Вектор сили 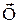який дорівнює добутку маси точки на вектор її прискорення називається даламберовою силою інерції і спрямований він протилежно до вектора прискорення.

Враховуючи (31.2), рівняння (31.1) набуває вигляду:

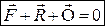. (31.3)

Вектор сили 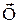який дорівнює добутку маси точки на вектор її прискорення, називається даламберовою силою інерції і спрямований він протилежно до вектора прискорення.

Рівняння (31.3) являє собою принцип Д’Аламбера для матеріальної точки:

Якщо до рухомої невільної матеріальної точки умовно прикласти її силу інерції, тоді геометрична сума заданих сил, реакцій в’язей і умовно прикладеної сили інерції дорівнюватиме нулю.

Отже, за допомогою принципу Д’Аламбера рівнянням динаміки можна надати форми рівнянь статики.

Сила інерції 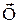– сила фіктивна. Вона, на відміну від фізичних сил, не має свого джерела виникнення.

Третій закон Ньютона рівності дії і протидії на силу інерції не поширюється.

Зауважимо, що даламберова рівновага є лише умовною моделлю або розрахунковою схемою дійсного абсолютного руху точки.

Фізично даламберових сил інерції в дійсності не існує.

Даламберові сили інерції прикладаються умовно, штучно, щоб надати рівнянням руху вигляд рівнянь рівноваги.

Такий метод складання рівнянь руху має назву метода кінетостатики і широко застосовується в інженерних розрахунках при визначенні динамічних реакцій опор твердих тіл.

31.2. Принцип Д’Аламбера для механічної системи

Розглянемо рух невільної механічної системи, що складається з 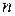матеріальних точок. В загальному випадку на кожну точку можуть діяти задані сили і реакції в’язей.

Застосуємо метод кінетостатики, а попередньо, принцип звільнення від в’язей до кожної точки системи, що розглядається:

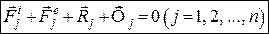. (31.4)

Тут 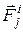– рівнодійна всіх прикладених до точки внутрішніх сил; 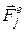– рівнодійна всіх прикладених до точки зовнішніх сил; 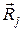– рівнодійна реакцій в’язей, накладених на цю точку; 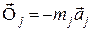– сила інерції точки.

Рівняння (31.3) являють собою принцип Д’Аламбера для механічноїсистеми, який формулюється так:

В рухомій невільній механічній системі в будь-який момент часу для кожної матеріальної точки системи геометрична сума прикладених до неї внутрішніх, зовнішніх сил, реакцій в’язей та її сили інерції дорівнює нулю.

Покажемо, що з принципу Д’Аламбера для механічної системи можна отримати два векторних або шість аналітичних рівнянь, які дозволяють розв’язувати задачі динаміки методами статики.

Підсумовуючи всі 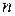рівнянь (31.4), отримаємо:

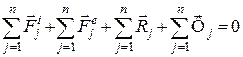
або

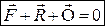. (31.5)

Тут – головний вектор всіх зовнішніх сил; 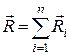– головний вектор реакцій в’язей; 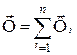– головний вектор сил інерції всіх точок механічної системи. За першою властивістю внутрішніх сил механічної системи маємо .

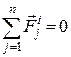З рівняння (31.5) випливає:

Для рухомої невільної механічної системи в будь-який момент часу геометрична сума головних векторів заданих сил, реакцій в’язей і сил інерції всіх точок цієї системи дорівнює нулю.

Якщо векторно домножити радіус-вектор 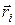точки 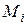на кожне з співвідношень (31.4) і підсумувати всі 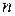рівнянь, то дістанемо:

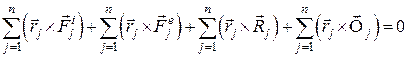
або

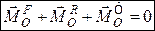. (31.6)

Тут 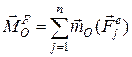– головний вектор-момент відносно центра 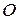всіх зовнішніх сил; 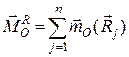– головний вектор-момент відносно центра 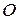реакцій в’язей; 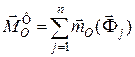– головний вектор-момент відносно центра О сил інерції всіх точок системи. За другою властивістю внутрішніх сил механічної системи маємо .

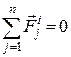З рівняння (31.6) випливає:

Для рухомої невільної механічної системи в будь-який момент часу сума головних векторів-моментів заданих сил, реакцій в’язей і сил інерції всіх точок системи відносно будь якого нерухомого центра дорівнює нулю.

Проектуючи векторні рівняння (31.5) і (31.6) на кожну з трьох координатних осей відповідно, отримаємо шість аналітичних рівнянь:

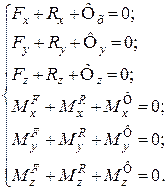(31.7)

Якщо задана механічна система складається з кількох з’єднаних тіл, то рівняння (31.7) можна записати окремо для кожного тіла.

31.3. Головний вектор і головний момент сил інерції

Застосування принципу Д’Аламбера для рухомої механічної системи вимагає вміння обчислювати головний вектор і головний вектор-момент сил інерції.

Знаючи вектори 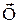та 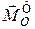та їхні проекції на кожну з трьох координатних осей, можна скласти рівняння (31.7) для зв’язаної механічної системи, що рухається прискорено, з яких потім визначити невідомі величини.

Сили інерції точок механічної системи у загальному випадку утворюють довільну просторову систему сил, яку за допомогою метода Пуансо можна привести до найпростішого вигляду.

Головний вектор сил інерції дорівнюватиме

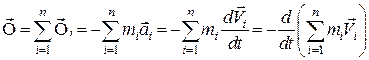. (31.8)

Запишемо формулу для визначення радіус-вектора центра мас механічної системи:

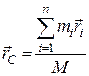, де ,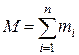

Похідна за часом:

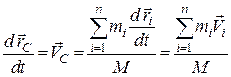звідки

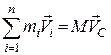Оскільки вираз в дужках формули (31.8) являє собою суму кількості руху точок заданої механічної системи, то зважаючи на попереднє, маємо:

Остаточно маємо:

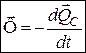. (31.9)

З іншого боку

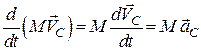
і тому

. (31.10)

Отже, головний вектор всіх сил інерції точок механічної системи дорівнює взятій з від’ємним знаком векторній похідній за часом від головного вектора кількості руху механічної системи (31.9), або взятим з від’ємним знаком добутку маси системи на вектор прискорення центра мас цієї системи (31.10).

Головний вектор-момент сил інерції відносно будь-якого нерухомого центра дорівнює

.

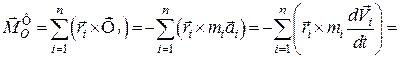
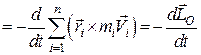Тут 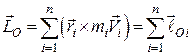– кінетичний момент механічної системи відносно нерухомого центра.

Таким чином, остаточно

. (31.11)

Отже, головний вектор-момент сил інерції точок системи відносно нерухомого центра дорівнює взятій з від’ємним знаком векторній похідній за часом від кінетичного моменту даної системи відносно того самого центра (31.11).

Лекція 32

ЗАСТОСУВАННЯ ПРИНЦИПУ Д’АЛАМБЕРА

32.1. Зведення сил інерції точок твердого тіла до найпростішого вигляду при поступальному, обертальному та плоскопаралельному русі

І. Поступальний рух тіла.

При поступальному русі твердого тіла всі його точки мають геометрично рівні швидкості і прискорення, які дорівнюють швидкості і прискоренню центра мас.

Приймемо центр мас тіла за центр зведення сил інерції. Оскільки обертання тіла навколо центра мас не відбувається, то головний вектор-момент сил інерції відносно центра мас дорівнюватиме нулю, тобто .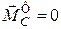

Отже, при поступальному русі твердого тіла сили інерції його точок зводяться до рівнодійної, що дорівнює головному вектору, яка прикладена в центрі мас тіла та має напрям, протилежний до напряму вектора прискорення:

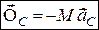. (32.1)

ІІ. Обертання тіла, що має площину матеріальної симетрії, навколо нерухомої головної центральної осі.

В цьому випадку центр мас тіла лежить на осі обертання і є нерухомим, тобто його прискорення 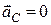, тоді:

.

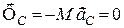Кінетичний момент тіла, що обертається відносно осі обертання, дорівнює:

.

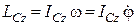При цьому головний вектор – момент сил інерції дорівнюватиме:

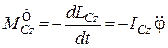
або

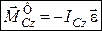.(32.2)

Отже, при обертанні твердого тіла навколо головної центральної нерухомої осі сили інерції точок тіла зводяться до пари сил, що лежить в площині матеріальної симетрії, а вектор – момент цієї пари дорівнює добутку момента інерції тіла на вектор кутового прискорення і має напрям, протилежно до напряму вектора кутового прискорення.

ІІІ. Плоскопаралельний рух твердого тіла, що має площину матеріальної симетрії.

Нехай тіло, що має площину матеріальної симетрії, рухається так, що всі його точки рухаються паралельно до цієї площини (рис. 32.1).

Цей рух можна розкласти на поступальний разом із центром мас т. С і на обертальний рух навколо рухомої осі , яка перпендикулярна до площини симетрії і проходить через центр мас.

Як відомо, при поступальному русі сили інерції зводяться до головного вектора , а при обертальному русі навколо головної центральної осі сили інерції зводяться до пари сил з вектором-моментом 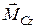, тобто тут маємо два фактори сил інерці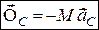ї:

і 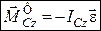. (32.3)

Отже, при русі твердого тіла, що має площину матеріальної симетрії, паралельно до цієї площини, сили інерції точок тіла зводяться до однієї сили, що лежить в площині матеріальної симетрії, яку прикладено в центрі мас, що дорівнює головному вектору сил інерції 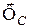, та до однієї пари сил, яка лежить в площині матеріальної симетрії, з вектор-моментом 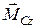, що дорівнює головному моменту сил інерції відносно рухомої осі 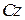, яка проходить через центр мас перпендикулярно до площини мате-ріальної симетрії тіла (рис. 32.1).

Приклад. Кільце, радіуса 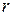і маси 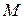, котиться без ковзання за прямолінійною дорогою, маючи в даний момент часу швидкість центра 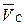та прискорення 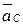(рис. 32.2). Знайти два фактори сил інерції, які діють на колесо в даний момент часу.

Розвязання. Точка дотику колеса і поверхні т.Р –МЦШ. Тоді 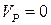. Т.С – центр мас колеса.

Враховуючи (32.3) маємо

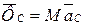та .

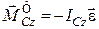Покажемо на рисунку їх напрямки.

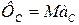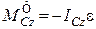За модулем і , де .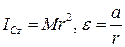

Тоді остаточно маємо .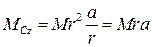

32.2. Визначення додаткових динамічних реакцій при русі зв’язаної механічної системи.

При русі невільної і-ої матеріальної точки повні реакції в’язей 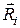складаються з статичних реакцій 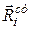і додаткових динамічних реакцій :

.

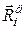Аналогічну рівність задовольняють також головні вектори і головні моменти реакцій в’язей при русі зв’язаного твердого тіла

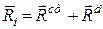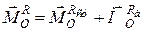; . (32.4)

При цьому статичні реакції задовольняють такі шість рівнянь:

;

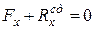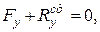
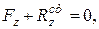
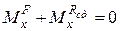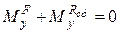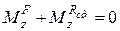; ; . (32.5)

Підставимо в рівняння кінетостатики (31.7) величини проекцій головного вектора і головного момента 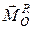реакцій в’язей, визначених рівністю (32.4):

; ;

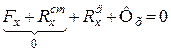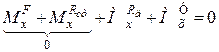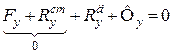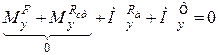; ; (32.6)

; .

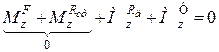Враховуючи в системі рівнянь (32.6) відповідно шість рівнянь (32.5), яким задовольняють статичні реакції, дістанемо рівняння для визначення додаткових динамічних реакцій опор рухомого твердого тіла:

; ;

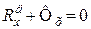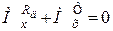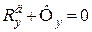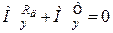; ; (32.7)

; .

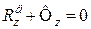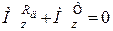Зазначимо, що при складанні рівнянь (32.7) не потрібно враховувати активні сили.

Отже, одним з найпростіших методів визначення додаткових динамічних реакцій є метод кінетостатики.

32.3. Приклад визначення додаткових динамічних реакцій підшипників при обертальному русі механічної системи навколо нерухомої осі

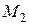Нехай механічна система складається з двох точкових тягарів і масою 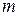, які розташовані на рівних відстанях 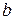від осі обертання 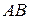(рис. 32.2). Задано: стала швидкість обертання системи , відстань між рівнями розташування тягарів – h, відстань між підп’ятником і шарніром . Система відліку обертаєтьсяразом з тягарями і невагомими стержнями, які їх підтримують.

Необхідно знайти динамічні реакції підшипників.

Розв’язання:

Однакові за модулем сили інерції тягарів дорівнюють:

.

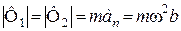За величиною момент пари сил інерції 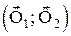дорівнює:

.

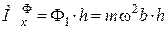Пара сил інерції може бути врівноважена лише парою, що лежить в тій самій або паралельній 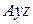площині. Такою парою є пара реакцій в’язей 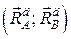що лежать у цій площині. За величиною момент цієї пари дорівнює:

<123 4 5 6 7 >

Дата добавления: 2014-12-20; просмотров: 696;