ВВОДНАЯ ЧАСТЬ

Московский университет имени С. Ю. Витте

КАФЕДРА МАТЕМАТИКИ И ИНФОРМАТИКИ

Мелкумян Б. В., Питерцева Г. А.

ВЫСШАЯ МАТЕМАТИКА

Курс лекций

Для дистанционного обучения

Студентов гуманитарных специальностей

МОСКВА 2012

Авторы – составители:

Мелкумян Б. В., Питерцева Г. А.

Высшая математика: Курс лекций.– М.: Московский университет им. С. Ю. Витте, 2012, _516_ стр.

Научный редактор:

Курс лекцийпредназначен для студентов дистанционной формы обучения гуманитарных специальностей.

Печатается по решению научно-методического совета Московского университета им. С. Ю. Витте.

© Б. В. Мелкумян, Г. А. Питерцева, 2012

© Московский университет им. С. Ю. Витте, 2012

ОГЛАВЛЕНИЕ

· Об авторах-составителях. 6

· От авторов-составителей. 6

ВВОДНАЯ ЧАСТЬ. 6

Что самое трудное в математике?. 7

Нужны ли способности?. 7

Что такое абстракция?. 7

Не затрудняет ли абстракция изучение математики?. 7

Цели и ожидаемые результаты курса. 8

Связь с другими дисциплинами. 8

План изучения курса. 9

График прохождения контрольных мероприятий: 10

ЛИТЕРАТУРА.. 11

Основной список. 11

Дополнительный список. 11

1. Алгебра высказываний. 11

1.1. Аксиоматический метод и его понятийный аппарат. 11

Определение. 11

Аксиома. Аксиоматический метод. 11

Доказательство. Теорема. 12

Особенность аксиоматического метода. 12

Основные методы доказательств. 12

Упражнения для самостоятельного анализа к Разделу 1: 13

Упражнение 1. 13

Упражнение 2. 13

Упражнение 3. 13

Упражнение 4. 14

Упражнение 5. 14

1.2. Алгебра высказываний. Основные законы математической логики. 14

Что есть высказывание. 14

Простые и составные высказывания. 15

Логические операции. 15

Порядок старшинства операций. 19

Основные законы математической логики. 20

Парадоксы логики. 20

Основная цель математической логики. 21

Задачи для самостоятельного решения. 22

1.3. Числа. 23

2. Матрицы. Действия с матрицами. 24

1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу). 25

2) Действие второе. Умножение матрицы на число. 26

3) Действие третье. Транспонирование матрицы.. 27

4) Действие четвертое. Сумма (разность) матриц. 28

5) Действие пятое. Умножение матриц. 29

6) Действие шестое. Нахождение обратной матрицы. 31

2.1. Вычисление определителей. 31

2.2. Вычисление обратной матрицы.. 36

2.3. Решение системы линейных уравнений. 42

Решение системы методом почленного сложения (вычитания) уравнений системы.. 46

2.4. Решение системы по правилу Крамера. 48

2.5. Решение системы линейных уравнений методом Гаусса (последовательного исключения неизвестных) 55

2.6. Несовместные системы. Системы с общим решением. Частные решения. 66

3. Комплексные числа. 77

Понятие комплексного числа. 78

Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел. 81

Сложение комплексных чисел. 81

Пример 1. 81

Вычитание комплексных чисел. 81

Пример 2. 81

Умножение комплексных чисел. 81

Пример 3. 82

Деление комплексных чисел. 82

Пример 4. 82

Пример 5. 83

Пример 6. 83

Тригонометрическая и показательная форма комплексного числа. 83

Пример 7. 84

Пример 8. 87

Возведение комплексных чисел в степень. 89

Пример 9. 89

Пример 10. 90

Пример 11. 90

Пример 12. 90

Пример 13. 91

Извлечение корней из комплексных чисел. 91

Пример 14. 91

Пример 15. 92

Как извлечь корень из произвольного комплексного числа?. 92

Пример 16. 92

Пример 17. 93

Решения и ответы: 95

4. Математические формулы и графики. 97

Математические формулы и таблицы.. 99

Горячие формулы школьного курса математики. 100

Калькулятор для автоматических расчетов. 100

Тригонометрические формулы.. 100

Тригонометрические таблицы.. 101

Графики и свойства элементарных функций. 101

Графики и основные свойства элементарных функций. 101

Как правильно построить координатные оси?. 101

Любой чертеж графика функции начинается с координатных осей. 101

Трехмерный случай. 103

Графики и основные свойства элементарных функций. 104

График линейной функции. 104

Пример 1. 104

График квадратичной, кубической функции, график многочлена. 107

Пример 2. 108

Таким образом, вершина находится в точке 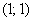....... 108

Кубическая парабола. 109

График функции 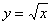............ 112

График гиперболы.. 114

График функции вида 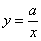( 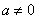) представляют собой две ветви гиперболы. 115

Пример 3. 115

Построить правую ветвь гиперболы 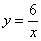......... 115

График показательной функции. 116

График логарифмической функции. 118

Обязательно нужно знать и помнить типовое значение логарифма: 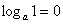. 118

Графики тригонометрических функций. 119

Построим график функции 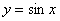.............. 119

График косинуса. 120

Построим график функции 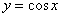.............. 120

В отличие от синуса в косинусе минус «бесследно пропадает». 120

Графики тангенса и котангенса. 121

Графики обратных тригонометрических функций. 122

Построим график арксинуса 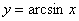................... 122

Построим график арккосинуса 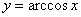................... 123

Арктангенс – функция нечетная: 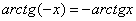. 125

· Об авторах-составителях

Мелкумян Баграт Владимирович – кандидат физико-математических наук, доцент. Читает лекции и проводит семинарские занятия в Московском университете им. С. Ю. Витте по различным разделам дисциплины «Математика» на факультетах экономики и финансов, управления и юридическом. Преподает дисциплины «Базы данных», «Проектирование информационных систем», «Разработка и стандартизация программных средств и информационных технологий» и «Физика» на факультете управления для специальности «Прикладная информатика в экономике» различных форм обучения. Область научных интересов связана с разработкой лазерных устройств и использованием методов математической физики в системах управления.

Питерцева Галина Александровна – кандидат технических наук, доцент, почетный профессор Московского университета им. С. Ю. Витте. Область научных интересов связана с использованием математических методов в экономике РФ. В 2006 году была награждена знаком «Отличник высшего и профессионального образования». Читает лекции и проводит семинарские занятия по дисциплине «Математика» на факультетах экономики и финансов, управления, подготовительных курсах. Является автором курсов лекций и комплекса учебно-методических материалов по Математике для студентов и абитуриентов. Является разработчиком банков тестовых заданий по Математике для центра тестирования и для вступительных экзаменов.

· От авторов-составителей

Математика является точной абстрактной наукой, изучающей количественные соотношения и пространственные формы. Точность математики означает, что основным методом в математических исследованиях являются строгие логические рассуждения. В древности областями применения математики были: землемерие, счет, торговля, архитектура и астрономия. В XVII-XVIII вв. появилась «Высшая математика» с направлениями аналитической геометрии, векторной и матричной алгебры, дифференциального исчисления, интегрального исчисления, дифференциальных уравнений, и т. д. В XIX-ХХ вв. на основе математики развиваются новые дисциплины: теория информации, теория оптимального управления и математическое программирование. В XX-XXI вв., благодаря быстродействующим вычислительным машинам, в использовании математических методов произошел качественный скачок.

Математическое мышление неудержимо проникает в практику экономических и гуманитарных наук, и следует быть к этому готовым.

Эти лекции предназначены для слушателей гуманитарных специальностей, изучающих курс математики в соответствии с учебными программами Московского университета им. С. Ю. Витте. Лекции курса дополняются примерами решения задач и контрольными упражнениями, которые облегчают понимание, показывают пользу теории, а также ликвидируют общеизвестную боязнь перед математикой.

ВВОДНАЯ ЧАСТЬ

Наш курс не отвечает на вопрос: ЗАЧЕМ НУЖНА ВЫСШАЯ МАТЕМАТИКА? Действительно, большинству из вас она никогда не потребуется. Это факт. Но изучение высшей математики предусмотрено учебными планами практически всех ВУЗов, и появляются задания, контрольные работы, которые необходимо сдавать. Тоже факт. Предлагаемый курс отвечает на вопрос: КАК ЭТО РЕШАТЬ?

Лекции носят сугубо практическую направленность, и при изучении той или иной темы мы даже не всегда вам расскажем, ЧТО ЭТО ТАКОЕ и не всегда дадим строгие математические определения.

Но на глобальный вопрос ответим. Один раз. Так ЗАЧЕМ ЖЕ НУЖНА ВЫСШАЯ МАТЕМАТИКА? Изучение высшей математики очень хорошо развивает интеллект, как «фитнес для ума». Если Вы освоили высшую математику, то сможете разобраться в любом предмете, в любой профессиональной деятельности. А может, и станете олигархом, или председателем кабинета министров, как Сергей Юльевич Витте, который имел математическое высшее образование.