Обобщение и ограничение понятий

Обобщение – этологическая операция, состоящая в переходе от понятия с меньшим объёмом, но с большим содержанием, к понятию с большим объёмом, но меньшим содержанием

Пример обобщения:

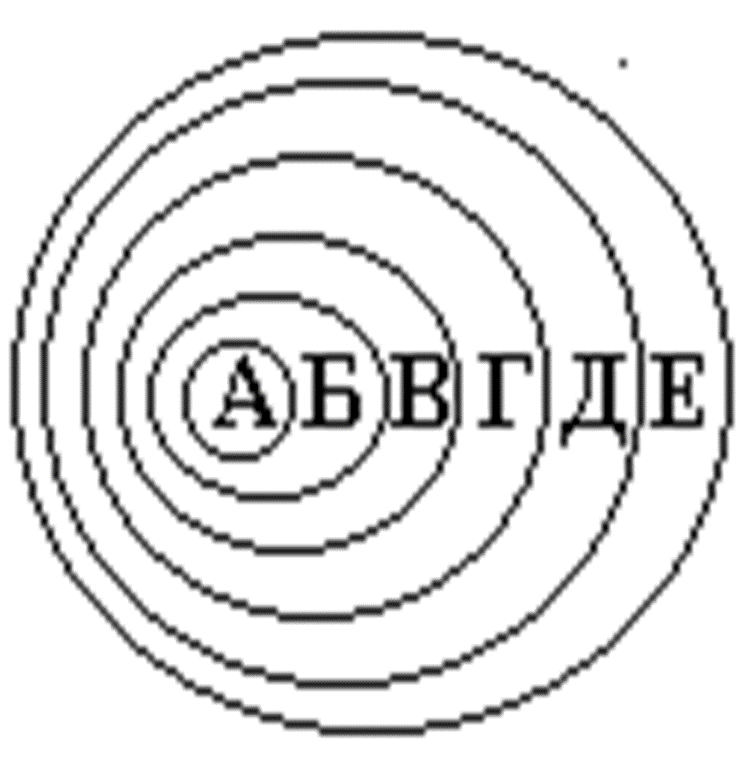
роза (А) - цветок (Б) - растение (В) - живой организм (Г) - организм (Д) - предмет (Е)

На схеме этот процесс обобщения выглядит следующим образом:

Ограничение – это логическая операция перехода от понятия с большим объёмом, но с меньшим содержанием, к понятию с меньшим объёмом, но большим содержанием

Пример ограничения:

- произведение музыкального искусства (Е) - опера (Д)

- опера русского композитора (Г)

- опера русского композитора XIX века (В)

- опера Мусоргского Модеста Петровича (Б) - опера Мусоргского М. П. «Хованщина» (А)

Пределом ограничения является единичное понятие с одним элементом объёма: в нашем случае это понятие А - опера «Хованщина»

Можно обе рассматриваемые нами операции изобразить и такой схемой:

Назначение операций обобщения и ограничения заключается в том, что они придают определённость мышлению, подчиняя его элементарным правилам:

1) обобщение правильно, если мысль осуществляет переход от видового понятия к родовому;

2) ограничение правильно, если мысль осуществляет переход от родового понятия к видовому

ЗАПОМНИТЕ:

ОПЕРАЦИИ ОБОБЩЕНИЯ И ОГРАНИЧЕНИЯ ОСУЩЕСТВЛЯЮТСЯ ТОЛЬКО МЕЖДУ ПОНЯТИЯМИ, КОТОРЫЕ НАХОДЯТСЯ В ОТНОШЕНИЯХ ПОДЧИНЕНИЯ

Логические ошибки:

1) Обобщение и ограничение часто смешивают с мысленным переходом от части к целому и выделением части из целого

2) Ограничение понятий часто происходит с помощью добавления признака: «студент» - «добросовестный студент».

Но имейте в виду, что нередко добавление эпитета не ведёт к ограничению понятия и является излишним:

«девушка» - «молодая девушка» (а кто видел старых девушек?),

«шар» - «круглый шар» (а какие ещё шары бывают?)

Данная ошибка называется плеоназмом (излишеством)

Деление понятий

Для упорядочения знания,поиска закономерных связей и уточнения смысла многих слов человеческим мышлением используется такая интеллектуальная процедура как классификация

Классификация – это распределение предметов какого-либо рода на взаимосвязанные группы (классы) согласно наиболее существенным признакам, присущим предметам данного рода и отличающим их от предметов других родов; при этом каждый класс занимает в получившейся системе своё постоянное, определённое место

В основе любой классификации лежит такая логическая процедура как деление понятий – это логическая операция, раскрывающая объём понятия

Структура деления:

1) Делимым называется родовое понятие, в объёме которого выделяются возможные виды

2) Основание деления – признак, в соответствии с которым выделяются члены деления

3) Члены деления – полученные в результате самой операции соподчинённые виды

Виды деления:

1) Деление по наличию или отсутствию признака, служащего основанием деления (его называют часто дихотомическим делением)

2) Деление по видоизменению признака, положенного в основание этой операции

3) Смешанное деление, когда используются оба вида деления одновременно

Примеры дихотомического деления:

· государства можно разделить на демократические и недемократические,

· людей – на счастливых и несчастливых,

· школьников – на добросовестных и недобросовестных,

· предпринимателей – на удачливых и неудачливых,

· граждан – на дееспособных и недееспособных

Право может быть оформлено (признак – форма выражения) в виде:

· правового обычая,

· юридического прецедента,

· нормативного акта,

· международного договора

Людей по социально-классовому признаку можно разделить на:

· крестьян,

· наёмных работников,

· предпринимателей,

· лиц свободных профессий

Смешанное деление, когда используются оба вида деления одновременно
Пример:

1) политические институты делятся на государственные и негосударственные;

2) среди негосударственных различаются партийные и непартийные;

3) непартийные же включают в себя профессиональные, женские, молодёжные, спортивные, художественные и так далее

Основные правила и ошибки деления:

1) Правило соразмерности

2) Правило исключения

3) Правило одного основания:

4) Правило непрерывности

1)Правило соразмерности – объединение объёмов членов деления должно совпадать с объёмом делимого понятия или объём делимого должен полностью исчерпываться членами деления. (А = В1 + В2 + В3 + ... + Вn)

Это означает, что при делении:

a) не должно быть пропущено ни одного предмета из объёма делимого понятия;

b) не должно появиться ни одного лишнего члена деления

Если данное правило не соблюдается, то возможны две основные ошибки: