Прямолинейно-параллельный фильтрационный поток
Фильтрационный поток называется прямолинейно- параллельным, когда траекториями частиц жидкости являются прямые линии, параллельные между собой, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения равны друг другу.
Наглядным примером такого фильтрационного потока является приток жидкости от прямолинейного контура питания к параллельной к нему прямолинейной батарее скважин, вскрывающих горизонтальный пласт постоянной ширины В на всю его толщину h =const. (рис. 6);
здесь: Рк - давление на контуре питания; Lк – расстояние от контура питания до батареи скважин (галереи).
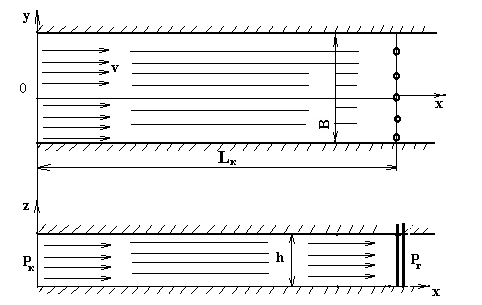
Рис.6
Законы движения частиц жидкости вдоль всех траекторий такого потока совершенно одинаковы, а поэтому для исследования принимаем одну из траекторий, по которой направляем координатную ось ОX, а ось ОY - вдоль контура питания.
Дифференциальное уравнение Лапласса (3.3) в данном случае принимает вид
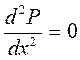 . (3.7)
. (3.7)
Для определения давления в любой точке потока дважды интегрируем уравнение (3.7) при следующих граничных условиях :
при X = 0 P = Pk = const ;
при X = Lk P = Pг = const . (3.8)
В результате двухкратного последовательного интегрирования (3.7) находим
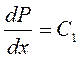 или
или 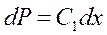 ,
,
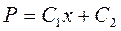 , (3.9)
, (3.9)
где С1 и С2 - произвольные постоянные. Подставляя в (3.9) граничные условия (3.8), получаем
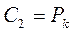 ; . (3.10)
; . (3.10)
Закон распределения давления находим, подставив значения С1 и С2 из (3.10) в выражение общего решения (3.9)
. (3.11)
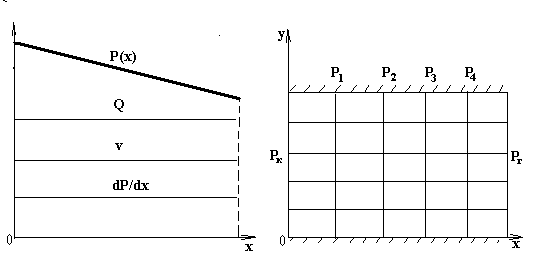 |
Как следует из решения (3.11) пластовое давление Р(x) распределяется вдоль линии тока по линейному закону (рис. 7). В любой плоскости YOZ давление одинаково во всех точках, для которых X = const, т.е. это есть уравнение семейства изобар, перпендикулярных к линии тока OX; изобары и линии тока образуют два семейства взаимно перпендикулярных прямых линий (рис. 8).
Рис.7 Рис.8
Из (3.11) получаем выражение для градиента давления
. (3.12)
Уравнение движения для рассматриваемого случая, как это следует из (3.2), имеет вид:
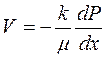 . (3.13)
. (3.13)
Подставив (3.12) в уравнение (3.13), находим выражение скорости фильтрации
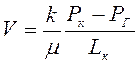 . (3.14)
. (3.14)
Объемный расход жидкости в потоке определяется произведением скорости фильтрации V на площадь поперечного сечения потока w = В*h, т.е
 . (3.15)
. (3.15)
Как видно из решений (3.12), (3.14) и (3.15) градиент давления dP/dx, скорость фильтрации V и расход (дебит) жидкости Q постоянны вдоль потока, т.е. не зависят от координаты X (рис. 7).
Закон движения частиц жидкости Х=Х(t) найдем, используя соотношение между скоростью фильтрации V и средней скоростью движения частиц жидкости VД
или 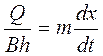 ;
;
откуда 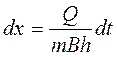
Интегрируя в пределах от 0 до t и от 0 до Х, получаем закон движения частиц жидкости
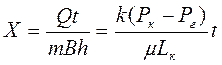 , (3.16)
, (3.16)
т.е. зависимость х =х(t) линейная, как и следовало ожидать, поскольку в рассматриваемых условиях фильтрационный поток движется с постоянной скоростью V (3.14).
Дата добавления: 2019-10-16; просмотров: 708;
