Дифференциальное уравнение установившейся фильтрации несжимаемой жидкости
Вывод дифференциального уравнения установившейся фильтрации несжимаемой жидкости по закону Дарси строится на основе уравнения неразрывности, уравнений движения и уравнений состояния жидкости и пористой среды.
В рассматриваемом случае (r = const) без учета деформации пористой среды (m = const) уравнение неразрывности (2.11) принимает вид
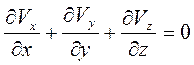. (3.1)
Уравнения установившегося движения жидкости по закону Дарси (2.4) в поле силы тяжести принимают вид
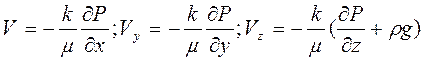. (3.2)
По уравнениям (3.2) находим производные
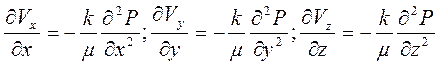
и подставляем их выражения в уравнение (3.1), получаем
,
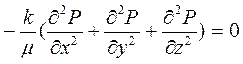откуда
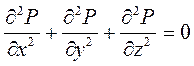, (3.3)
т.е. Ñ2 P=0, или divgradP=0 . (3.4)
Если ввести потенциал скорости фильтрации (2.6)
Ф =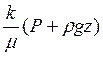 
и подставить в уравнения движения (3.2), то последние принимают вид
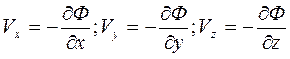. (3.5)
Дифференцируя (3.5) по соответствующим координатам и подставляя результаты в уравнение (3.1), получим
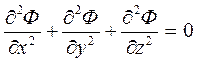, (3.6)
т.е потенциал скорости фильтрации Ф(x,y,z) так же, как и давление Р(x,y,z), удовлетворяет уравнению Лапласса. Функции, удовлетворяющие уравнению Лапласа, являются непрерывными, имеющими непрерывные частные производные первого и второго порядка, называются гармоническими.
Решения уравнения Лапласса, как решения линейного однородного дифференциального уравнения, имеют следующие свойства:
1) произведение частного решения на произвольную постоянную, есть также решение этого уравнения;
2) сумма частных решений есть также решение этого уравнения;
Если, например, Р1, Р2, Р3,...., Рn - есть решения уравнения (3.3), то функция
Р =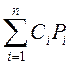 
, где Сi – const
также удовлетворяет уравнению (3.3).
На основе дифференциального уравнения (3.3) или (3.6) исследуются фильтрационные характеристики всех (трех) одномерных фильтрационных потоков несжимаемой жидкости в недеформируемой пористой среде:
1) прямолинейно-параллельный;
2) плоско-радиальный;
3) радиально-сферический.
Одномерным называется фильтрационный поток жидкости, в котором скорость фильтрации и напор(давление) являются функциями только одной координаты, отсчитываемой вдоль линии тока.
Задача исследования установившегося фильтрационного потока заключается в определении законов распределения давления, скорости фильтрации и расхода (дебита) жидкости, а также в определении закона движения частиц жидкости вдоль их траектории.
Ниже производятся исследования отмеченных выше фильтрационных потоков несжимаемой жидкости в однородных коллекторах.
Дата добавления: 2019-10-16; просмотров: 488;