Распределение Максвелла.

Полная энергия системы равна сумме ее потенциальной и кинетической энергий.

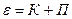
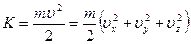
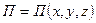
Рассмотрим распределение Больцмана, в котором энергия системы представлена в виде суммы двух слагаемых. По свойству потенциальной функции, выражение можно разложить на произведение двух сомножителей, каждый из которых является функцией определенного вида энергии:

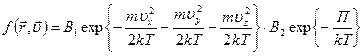
В таком виде выражение называется функцией распределения Максвелла-Больцмана. Сомножитель, зависящий от кинетической энергии, называется функцией Максвелла, а сомножитель, зависящий от потенциальной энергии – функцией Больцмана.

Найдем вероятность того, что молекула имеет скорость в интервале .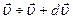

Плотность вероятности этого – функция распределения Максвелла.

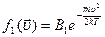
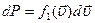
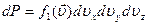
Определим константу 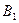из условия нормировки: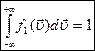

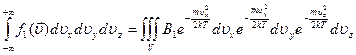, так как компоненты скорости независимы, то

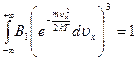. Обозначим константу 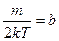, , 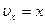тогда после замены мы получим табличный интеграл:

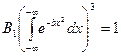, значение интеграла 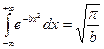, отсюда получим

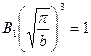, следовательно:

.

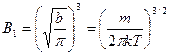Таким образом 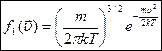- плотность вероятности молекул иметь скорость в интервале от 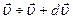, распределение молекул по проекциям координат.

Теперь найдем вероятность того, что молекулы имеют скорость в интервале 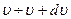по абсолютному значению (по модулю). Для этого перейдем от распределения проекций скоростей к распределению по модулю скорости. Удобнее переход сделать в системе сферических координат.

Оператор Лапласа дает коэффициент перехода от декартовой системы координат к сферической:

,

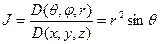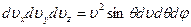
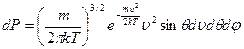
Нас интересуют только абсолютные значения, поэтому:

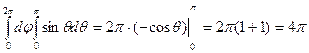, с учетом вычисленных интегралов:

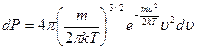, отсюда плотность вероятности:

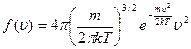
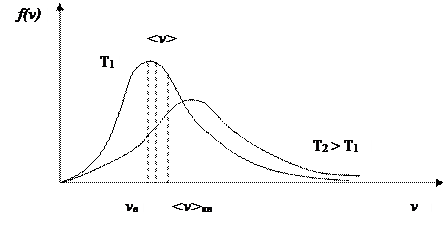
Зная плотность распределения молекул по абсолютному значению скорости, мы можем рассчитать три характеристические скорости движения молекул идеального газа.

Средняя арифметическая скорость:

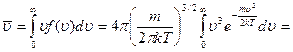выделим для замены переменной

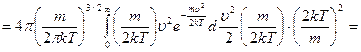
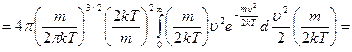сделаем замену переменной

и учтем, значение табличного интеграла: 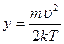, , 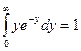получим после сокращения констант:

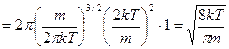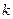, где - постоянная Больцмана, 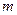- масса молекулы, преобразуем, умножив числитель и знаменатель дроби на число Авогадро:

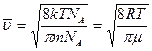, где 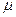- молярная масса компоненты системы.

Результат: 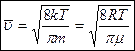- средняя арифметическая скорость движения молекул идеального газа.

Средняя квадратичная скорость:

,

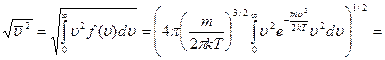сделаем замену переменной:

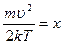, тогда 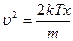, , 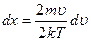отсюда ,

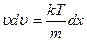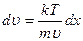, разделим переменные и найдем связь между 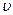и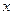

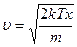, подставим полученное значение в дифференциал:

, .

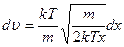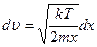Подставим все в интеграл:

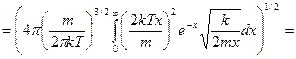преобразуем,

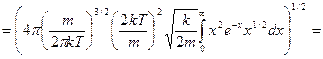
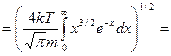, учтем значение табличного интеграла: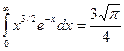

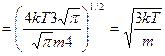, таким образом

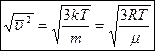- средняя квадратичная скорость.

Наиболее вероятная скорость:

Наиболее вероятная скорость – это скорость, соответствующая максимуму кривой распределения молекул по скоростям, т.е. должно выполнятся условие:

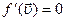
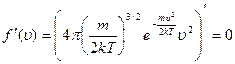
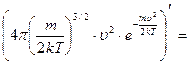обозначим константу 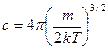и найдем производную произведения

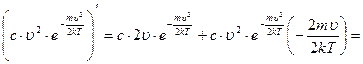
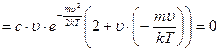
так как величина 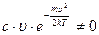, то должно выполняться условие:

, ,

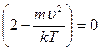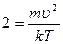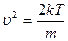
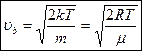- скорость наиболее вероятная.

При комнатной температуре средняя арифметическая скорость движения молекул:

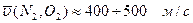, а характеристические скорости водорода в 4 раза больше.

Как посчитать число молекул, скорости которых лежат в заданном диапазоне?

Если 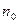- число молекул в единице объема, то 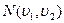- число молекул, скорости которых распределены в интервале от 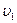до 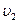равно:

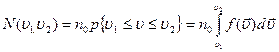, если учесть что 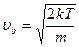, и введя переменные 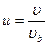, , 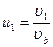, 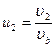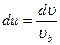то

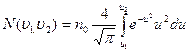- такой вид более нагляден, для анализа формы кривой распределения Максвелла. В книгах имеются таблицы интеграла: 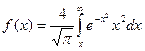с их помощью упрощаются вычисления величины .

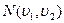Из таблиц в частности находим, что:

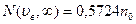
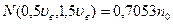
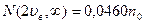
Т.о. большая часть молекул имеет скорости в сравнительно небольшом интервале около наиболее вероятной, а молекул со скоростями вне этого интервала сравнительно мало.

Для экспериментальной проверки было проделано много опытов. Самый известный – опыт Штерна (1920). На оси двух коаксиальных цилиндров ( 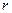и 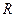) расположена платиновая нить, покрытая слоем 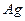. Нить нагревали током, серебро испарялось, и его атомы хаотично вылетали по всем радиальным направлениям. При этом они имели и различные скорости движения. Воздух внутри цилиндров откачивался, чтобы столкновения молекул серебра с молекулами воздуха не искажали картину. Атомы серебра равномерно покрывали поверхность внешнего цилиндра, что указывало на равновероятность всех направлений их скорости. Затем во внутреннем цилиндре - узкая щель, диафрагмирующая пучок атомов по направлению (скорости любые по величине). Внешний цилиндр приводили во вращение ( 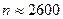) об/мин.

В зависимости от скорости атомы попадают на разные участки поверхности вращающегося цилиндра, согласно формуле на участок АВ:

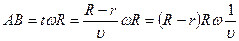Þ .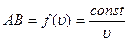

Чем больше атомов осаждается на стенке, тем толще пленка. Измеряя толщину пленки, можем определить число атомов, обладающих скоростью, лежащей в некотором диапазоне, т.е. построить диаграмму, которая при сглаживании схожа с кривой распределения Максвелла .