Вывод выражения для излучательной способности.
Это выражение впервые было получено М.Планком, который, опираясь на известный ему экспериментальный материал, предположил, что энергия световой волны пропорциональна не квадрату ее амплитуды, а частоте n, т.e. Есв = hn , где h - коэффициент пропорциональности, известный теперь как постоянная Планка ( h = 6,62× 10 -34 Дж сек.), причем про-цесс излучения происходит не непрерывно, а отдельными порциями - квантами. В связи с этим предположением энергия диполей также изменяется скачком от E1 до Е2. Однако мы приведем более простой вывод, принадлежащий А.Эйнштейну. Основная идея этого вывода состоит в том, что кроме спонтанных актов излучения, происходящих с вероятностью А i k существуют вынуженные элементарные акты излучения и поглощения под действием внеш-ней периодической силы, вероятности которых Вi k или Вk i , в зависимости от направления перехода.
Рассмотрим систему, состоящую из большого числа (No) диполей, находящуюся в сос-тоянии равновесия с тепловым излучением, спектральная плотность энергии которого( т.е. излучательная способность) равна en,Т .
Обозначим энергию диполя до момента излучения через E1, a энергию диполей после излучения – E2 ; число диполей в состояниях е1 и Е2 - через N1и N2 . Количество спонтанных переходов из состояния с энергией е1 в состояние с энергией Е2 равно D 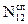 = A12 N1 .B то же время под действием теплового излучения, характеризующегося излучательной способ-ностью en,Т происходят вынужденные переходы как из состояния 1 в состояние 2, так и обратно.Число этих переходов равно D
= A12 N1 .B то же время под действием теплового излучения, характеризующегося излучательной способ-ностью en,Т происходят вынужденные переходы как из состояния 1 в состояние 2, так и обратно.Число этих переходов равно D 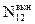 = n1В12 en,Т , D
= n1В12 en,Т , D 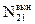 = N2 B21en,Т .
= N2 B21en,Т .
В состоянии теплового равновесия число переходов из состояния I в состояние 2 должно равняться числу переходов из состояния 2 в состояние l.Ha основании этого запишем D 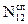 + D
+ D 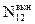 = D
= D 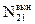 или А12N1 +n1В12 en,Т = N2 B21en,Т .
или А12N1 +n1В12 en,Т = N2 B21en,Т .
Отсюда находим en,Т :
en,Т = 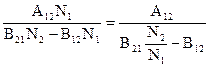 .
.
Для оценки отношения N2 / n1 используем представления классической статистики, позволяющей на основании распределения Больцмана вычислить число частиц с заданной энергией:
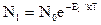 ;
; 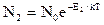 , где N0 -общее число частиц в системе. Отсюда
, где N0 -общее число частиц в системе. Отсюда
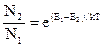 .
.
Тогда с учетом того, что, как показывает эксперимент,В12 =В 21 , получим
en,Т = 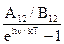 .
.
В последнем выражении использовано представление Планка, что E1 –E2 = hn. Отношение A12 / B12 не может быть вычислено в нашем курсе. Строгий расчет показывает, что оно рав-но hn3 /с2 , где с – скорость света. Поэтому выражение для излучательной способности при-обретает следующий вид:
en,Т = 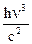
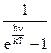 .
.
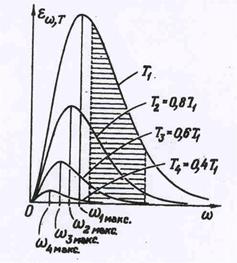 Рис.61 Зависимость излучатель-
ной спосбности от частоты и
температуры.
Рис.61 Зависимость излучатель-
ной спосбности от частоты и
температуры.
| Графическая зависимость излучательной способности приведена на рис.61, где по оси частот отложена угло-вая частота w =2nn.
§ 13-3 Законы Стефана- Больцмана и Вина.
Из рис.61 видно, что для каждой температуры излучательная способность имеет максимальное значение при определенной частоте излучения. Для определения этой частоты проведем исследова-ние на экстремум величины en,Т , предварительно проведя замену перемен-ной в целях сокращения записи. Введем новую переменную х:
х = 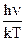 ;
тогда n = ;
тогда n = 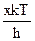 ; n3 = ; n3 = 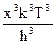 и dn = и dn = 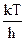 dx .
Теперь выражение для излучательной способности приобретает такой вид: dx .
Теперь выражение для излучательной способности приобретает такой вид:
|
en,Т = 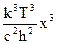
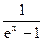 .
.
Вычисляя первую производную и сокращая полученный результат на постоянную величи-ну, имеем:
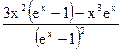 = 0.
= 0.
Из этого выражения видно, что оно равно нулю, если числитель дроби равен нулю, откуда для определения экстремального значения х получаем трансцендентное уравнение:
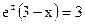 .
.
Можно показать,что это уравнение имеет решение (приближенное значение х м =2,8214 ), для простоты обозначим его а',т.е. х М = а', или hnМ / kT = а', откуда следуетзакон Вина:
nМ =аТ.
В этом выражении постоянная а является комбинацией других постоянных: а = a’ , k / h .
Определим интегральную излучательную способность Ет (она называется энергети-ческой светимостью) как еT = 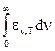 , или в обозначениях новой переменной:
, или в обозначениях новой переменной:
ET = 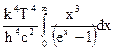 .
.
Интеграл в этом выражении является табличным,его величина равна л4 / 15.0бозначая через s комбинацию постоянных 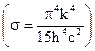 получаем следующее выражение для энергети-ческой светимости: ЕТ = sТ4, которое известно как законСтефана-Больцмана.
получаем следующее выражение для энергети-ческой светимости: ЕТ = sТ4, которое известно как законСтефана-Больцмана.
Сравним теоретические выводы с практикой.Экспериментальные данные показывают, .что при комнатной температуре максимум излучения лежит в далекой инфракрасной об-ласти, излучение в видимой области практически отсутствует. При температуре, приближающейся к 1000 К, максимум по-прежнему в инфракрасной области, однако и из-лучение в видимой части спектра становится заметным ( см.рис.61). В силу того, что интен-сивность от длинных, красных волн, к коротким, фио-летовым, падает, наибольшая интен-сивность излучения приходится на красную часть спектра - это температура «красного каления». По мере роста температуры различие в интенсивностях падает, излучение приоб-ретает желтый, а затем белый цвет. При температуре между 5000 и 6000° К максимум про-ходит через область спектра, к которой человеческий глаз наиболее чувствителен. Тем-пературе 5900 К отвечает температура поверхности Солнца, лучеиспускательная способ-ность которого близка к лучеиспускательной способности абсолютно черного тела. Такое излучение воспринимается глазом как белый, дневной свет. При более высоких темпера-турах максимум смещается в ультрафиолетовую область, а интенсивность в фиолетово - голубой области становится большей, чем в красной. Излучение приобретает голубой отте-нок.
Теория атома Бора.
Изучая прохождение а-частиц (ядер атомов гелия) через тонкую золотую фольгу, английский ученый Э.Резерфорд обнаружил, что большинство этих частиц свободно прохо-дит через многочис-ленные слои атомов, и вещество в этих экспериментах ведет себя как крупное сито.свободно пропускающее довольно тяжелые заряженные частицы. Для объяс-нения полученных результатов Резерфорд разработал так называемую планетарную модель атома, где основная масса сосредоточена в ядре, размеры которого крайне малы,а электро-ны, входящие в состав атома, вращаются вокруг этого ядра. Планетарная модель хорошо объясняла поведение а- частиц, но противоречила выводам классической физики: двигаясь с ускорением любая заряженная частица должна излучать электромагнитные волны. Энергия электрона в этом случае должна быстро уменьшаться,и он должен упасть на ядро.
Датский физик Н.Бор сумел разрешить это противоречие, сформулировав три постулата, которые легли в основу боровской теории строения атома. Эти постулаты гласили:
1.в атоме существуют стационарные орбиты, на которых электрон не излучает и не пог-лощает энергии,
2.радиус стационарных орбит дискретен; его значения должны удовлетворять условиямквантования момента импульса электрона:
m v r = n 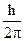 , где n - целое число,
, где n - целое число,
3.при переходе с одной стационарной орбиты на другую электрон испускает или поглощаетквант энергии, причем величина кванта в точности равна разности энергий этих уровней:
hn = E1 – Е2.
Из этих постулатов видно,что фактически Бором были введены новые - квантовые представления о свойствах электрона в атоме. Покажем,что в этих предположениях энергия элек-трона также становится дискретной (квантуется).
Пусть Ze - заряд ядра атома, вокруг которого вращается один электрон массы m. Радиус орбиты обозначим г, а скорость электрона на орбите - v. Тогда уравнение движения электрона можно записать в следующем виде:
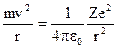 ,
,
где сила, стоящая в правой части этого уравнения, представляет собой кулоновскую силу взаимодействия двух зарядов: е и Ze, a величина v2 /r характеризует центростремительное ускорение электрона. Сокращая знаменатели обеих частей этого уравнения и используя выражение второго постулата Бора, получаем систему из двух уравнений, где неизвестными являются скорость v и радиус орбиты r :
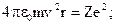
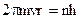 .
.
Деля почленно одно уравнение на другое, получаем: v = 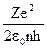 .Подставим выражение
.Подставим выражение
для скорости во второе уравнение нашей системы и найдем выражение для радиуса орбиты:
r = 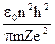 .
.
Общая энергия электрона на орбите складывается из его кинетической энергии и потен-циальной энергии его взаимодействия с зарядом ядра:
Wo = Т кин + Uпот ,
или 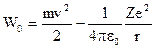 .
.
Знак минус отражает тот факт,что заряд электрона - отрицательный. Подставляя в это выражение полученные ранее значения скорости и радиуса, находим:
W0 = 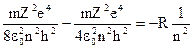 ,
,
где 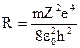 называют постоянной Ридберга .
называют постоянной Ридберга .
Таким образом общая энергия электрона в атоме оказывается отрицательной, и онаувеличивается с ростом n.
Частота излучения, которое соответствует переходу с орбиты номера n на орбиту с номером m, равна:
n = 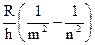 .
.
Если атомы являются изолированными и не участвуют в других взаимодействиях, то допускаемые частоты образуют набор отдельных спектральных линий, соответствующих различным значениям чисел n и m. Обычно такое состояние атомов наблюдается в газах. Каждому химическому элементу соответствуют свои спектральные линии - на этом основан спектральный анализ, позволяющий по наблюдаемому набору линий установить химичес-кий состав исследуемого объекта. При исследовании спектров испускания наблюдаются узкие светящиеся линии, а если свет проходит через холодный газ, то наблюдаются темные линии на тех местах, которые соответствуют положению линий излучения горячим газом. Эти темные линии называются спектрами поглощения.
При очень низких температурах электроны в атомах стремятся занять орбиты с наименьшими значениями энергии, но при конечных температурах за счет энергии теплового движения атомов электроны могут приобретать дополнительную энергию и переходить на более высоколежащие орбиты, степень заселенности которых определяется распределением Больцмана: чем выше значения энергии, тем меньшее количество электронов занимают данный уровень. Поэтому в обычном состоянии атомы больше поглощают электромагнитные волны ( набор разрешенных частот может лежать в любом диапазоне), чем излучают. Для того, чтобы процесс излучения преобладал над процессом поглощения, атому необходимо сообщать энергию. Приобретая эту энергию, атомы переходят в возбужденное состояние, но оно является энергетически невыгодным, и обычно через очень короткий промежуток времени электроны возбужденного атома переходят на орбиты с меньшей энергией. Процесс перехода является случайным, поэтому значение начальной фазы и направления колебаний векторов электрического и магнитного полей изменяются от одного атома к дру-гому хаотическим образом. Получающееся электромагнитное излучение является некоге-рентным. Однако существует возможность своебразной синхронизации процессов излуче-ния. Использование такой возможности определяет принцип действия генераторов корот-коволнового излучения - мазеров и лазеров.
Дата добавления: 2019-10-16; просмотров: 671;
