Диффузионные уравнения

Пусть вдоль полупроводника имеется градиент концентрации свободных носителей заряда, создание которого возможно с помощью освещения образца, его неравномерного нагрева и т.д.

В общем случае, ток проводимости состоит из геометрической суммы дрейфового и диффузионного токов.

Дрейфовые составляющие плотности тока проводимости определяются по закону Ома.

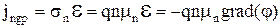, (3.6.1)

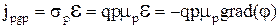, (3.6.2)

где 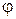- электрический потенциал, n и р концентрации электронов и дырок, которые в общем случае не являются равновесными.

Диффузионная составляющая тока зависит от градиента концентрации свободных носителей заряда

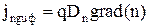, (3.6.3)

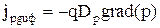. (3.6.4)

Диффузионный ток создает объемные заряды, поле которых вместе с внешним полем обуславливает дрейфовый ток.

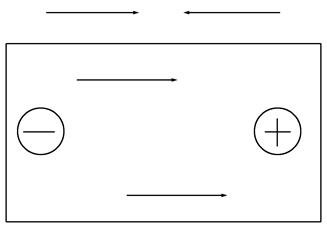
В представленном на рисунке 3.4 случае, когда p₁>p₂, левая часть будет заряжаться отрицательно, а правая положительно и внутреннее электрическое поле полупроводника, обусловленное объемными зарядами, направлено против внешнего поля.

В общем случае, ток носителей одного вида в полупроводнике равен сумме диффузионного и дрейфового тока:

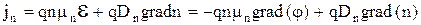, (3.6.5)

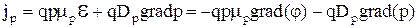. (3.6.6)

Если рассматривать токи в каком либо одном направлении, то уравнения (3.6.5), (3.6.6) можно переписать в виде

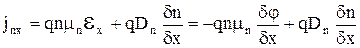, (3.6.7)

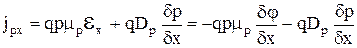. (3.6.8)

Полная плотность тока равна:

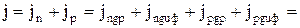
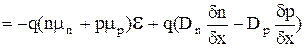. (3.6.9)

Направления токов определяют обычно в зависимости от направления градиентов потенциала j и концентраций. Знаки токов учитывают при записи уравнений.

Связь между дрейфовой подвижностью носителей и коэффициентами диффузии выражается с помощью уравнений Эйнштейна

Рис. 3.5

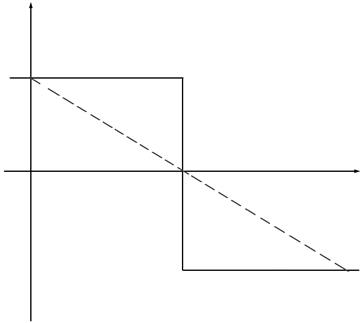
Рис. 4.1

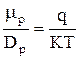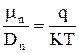, . (3.6.10)

Подвижность носителей пропорциональна коэффициенту диффузии.

Контактные явления