Эвольвента и ее свойства.

Эвольвента образуется путем перекатывания производящей прямой KyNy без скольжения по основной окружности радиуса rb.
Радиус произвольной окружности – ry. ONy || tt
Из треугольника ONyKy следует, что
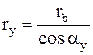 (1)
(1)
Т.к. KyNy перекатывается без скольжения по основной окружности, то 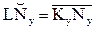
rb(qy + ay) = rb.tg ay
qy = tg ay - ay (2)
qy = inv ay
qy – инволюта;
Уравнения (1) И (2) являются уравнениями эвольвенты в параметрической форме.
aу – угол профиля эвольвенты для точки Ку, лежащей на произвольной окружности.
a – угол профиля эвольвенты для точки К, лежащей на делительной окружности радиуса r.
Угол профиля эвольвенты для точки Кb, лежащей на основной окружности, равен нулю: ab=0.
Свойства эвольвенты.
1. Форма эвольвенты зависит от радиуса основной окружности. При стремлении rb 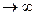 ,эвольвента превращается в прямую линию (пример рейка).
,эвольвента превращается в прямую линию (пример рейка).
2. Производящая прямая KyNy является нормалью к эвольвенте в данной тоске.
3. Эвольвента начинается от основной окружности. Внутри основной окружности точек эвольвенты нет.
§4.4 Элементы эвольвентного зубчатого колеса.
Делительной окружностью называется окружность стандартных шага р, модуля m и угла профиля a.
Шаг – расстояние между одноименными точками двух соседних профилей зубьев, измеренные по дуге соответствующей окружности.
Модулем называется часть диаметра делительной окружности, приходящаяся на один зуб.
Модуль m,[мм] – стандартная величина и определяется по справочникам, исходя из трех рядов:
1 ряд – наиболее предпочтительный;
2 ряд – средней предпочтительности;
3 ряд – наименее предпочтительный.
Модуль характеризует высоту зуба. Чем больше зуб, тем более шумной становится зубчатая передача.
Угол профиля – угол между касательной к эвольвенте в данной точке и радиус-вектором данной точки (см. чертеж эвольвенты).
Угол профиля для точки, лежащей на делительной окружности, является величиной стандартной и равной 20о(хотя лучше 25о).
Дата добавления: 2019-07-26; просмотров: 737;
