Применение линейной регрессии в прогнозировании
Прогнозирование - это самостоятельная отрасль науки, которая находит широкое применение во всех сферах человеческой деятельности. Существует большое разнообразие видов и способов прогнозирования, разработанных с учетом характера рассматриваемых задач, целей исследования, состояния информации. Этим вопросам посвящено много книг и журнальных статей. Покажем на примере линейной регрессии применение эконометрических моделей в прогнозировании значений экономических показателей.
В обыденном понимании прогнозирование - это предсказание будущего состояния интересующего нас объекта или явления на основе ретроспективных данных о прошлом и настоящем состояниях при условии наличия причинно-следственной связи между прошлым и будущим. Можно сказать, что прогноз - это догадка, подкрепленная знанием. Поскольку прогностические оценки по сути своей являются приближенными, может возникнуть сомнение относительно его целесообразности вообще. Поэтому основное требование, предъявляемое к любому прогнозу, заключается в том, чтобы в пределах возможного минимизировать погрешности в соответствующих оценках. По сравнению со случайными и интуитивными прогнозами, научно обоснованные и планомерно разрабатываемые прогнозы без сомнения являются более точными и эффективными. Как раз такими являются прогнозы, основанные на использовании методов статистического анализа. Можно утверждать, что из всех способов прогнозирования именно они внушают наибольшее доверие, во-первых, потому что статистические данные служат надежной основой для принятия решений относительно будущего, во-вторых, такие прогнозы вырабатываются и подвергаются тщательной проверке с помощью фундаментальных методов математической статистики.
Оценка параметров линейной регрессии представляет собой прогноз истинных значений этих параметров, выполненный на основе статистических данных. Полученные прогнозы, оказываются достаточно эффективными, так как они являются несмещенными оценками истинных параметров.
Применим модель линейной регрессии (8.2.4) с найденными параметрами (8.2.8) и (8.2.9) для определения объясняемой переменной 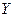 на некоторое множество ненаблюдаемых значений объясняющей переменной
на некоторое множество ненаблюдаемых значений объясняющей переменной 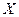 . Точнее говоря, поставим задачу прогнозирования среднего значения
. Точнее говоря, поставим задачу прогнозирования среднего значения 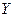 , соответствующего некоторому значению
, соответствующего некоторому значению 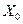 объясняющей переменной
объясняющей переменной 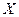 , которое не совпадает ни с одним значением
, которое не совпадает ни с одним значением 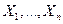 . При этом
. При этом 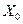 может лежать как между выборочными наблюдениями
может лежать как между выборочными наблюдениями 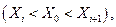 так и вне интервала
так и вне интервала 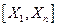
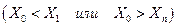 . Прогноз значения
. Прогноз значения 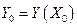 может быть точечным или интервальным. Ограничимся рассмотрением точечного прогноза, т.е. искомое значение определим в виде
может быть точечным или интервальным. Ограничимся рассмотрением точечного прогноза, т.е. искомое значение определим в виде
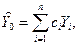 (8.5.1)
(8.5.1)
где 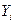 - наблюдаемые значения случайной величины
- наблюдаемые значения случайной величины 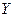 , а
, а 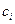 - коэффициенты (веса), которые должны быть выбраны так, чтобы
- коэффициенты (веса), которые должны быть выбраны так, чтобы 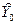 был наилучшим линейным несмещенным прогнозом, т.е. чтобы
был наилучшим линейным несмещенным прогнозом, т.е. чтобы 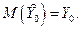
Из (8.5.1) для наблюдаемых значений
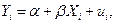
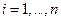
находим
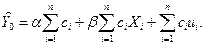
Так как по свойству математического ожидания ( (2.5.4) - (2.5.5))
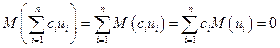 ,
,
то
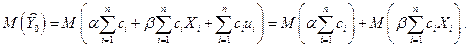
Но так как в правой части под оператором математического ожидания стоят только постоянные числа, то
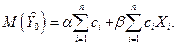
Учитывая соотношение 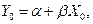 можем сказать теперь, что
можем сказать теперь, что 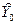 будет несмещенным линейным прогнозом для
будет несмещенным линейным прогнозом для 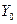 тогда и только тогда, когда
тогда и только тогда, когда
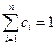 и
и 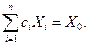 (8.5.2)
(8.5.2)
Следовательно, всякий вектор 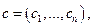 удовлетворяющий условиям (8.5.2), делает выражение (8.5.1) несмещенным линейным прогнозом величины
удовлетворяющий условиям (8.5.2), делает выражение (8.5.1) несмещенным линейным прогнозом величины 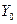 . Поэтому надо найти конкретное выражение весов
. Поэтому надо найти конкретное выражение весов 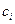 через известные нам величины. Для этого решим задачу минимизации дисперсии величины
через известные нам величины. Для этого решим задачу минимизации дисперсии величины 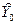 :
:
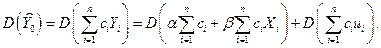
Так как под оператором дисперсии в первом слагаемом правой части уравнения стоят постоянные числа, то
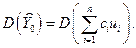
С учетом предположений b) и c) и пользуясь свойствами дисперсии (2.5.4) и (2.5.6), имеем:
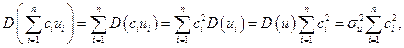
где 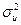 - среднеквадратическое отклонение случайной величины
- среднеквадратическое отклонение случайной величины 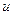 .
.
Составим оптимизационную задачу минимизации дисперсии 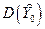 с ограничениями (8.5.2):
с ограничениями (8.5.2):
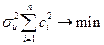
при ограничениях
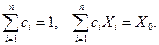
Так как множитель 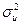 не зависит от
не зависит от 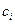 и не влияет на минимальное значение целевой функции, то функцию Лагранжа (см. (2.3.8) ) сконструируем следующим образом:
и не влияет на минимальное значение целевой функции, то функцию Лагранжа (см. (2.3.8) ) сконструируем следующим образом:
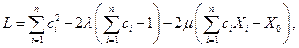
где 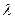 и
и 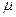 - множители Лагранжа. Необходимые условия оптимальности точки
- множители Лагранжа. Необходимые условия оптимальности точки 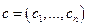 имеют вид (см. (2.3.9)):
имеют вид (см. (2.3.9)):
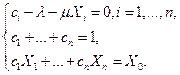 (8.5.3)
(8.5.3)
Просуммировав первое уравнение по 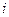 , с учетом второго уравнения получим:
, с учетом второго уравнения получим:
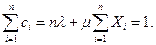
Отсюда находим множитель Лагранжа
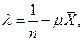
где 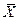 - среднее значение случайной величины
- среднее значение случайной величины 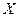 . Полученное значение
. Полученное значение 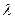 вновь подставим в первое уравнение системы (8.5.3) и найдем
вновь подставим в первое уравнение системы (8.5.3) и найдем
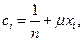
где 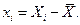 Обе части полученного выражения умножим на
Обе части полученного выражения умножим на 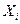 и вновь просуммируем по
и вновь просуммируем по 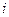 . Тогда, с учетом третьего уравнения в (8.5.3) , получим:
. Тогда, с учетом третьего уравнения в (8.5.3) , получим:
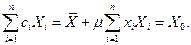
Отсюда найдем другой множитель Лагранжа:
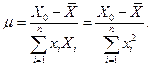
(здесь мы учли тот факт, что 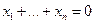 ). Следовательно,
). Следовательно,
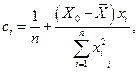
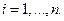
Подставляя эти значения в (8.5.1) , получим несмещенную линейную оценку. Конкретный вид этой оценки имеет вид:
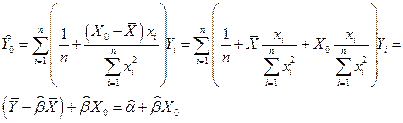
(в последних двух преобразованиях использованы соотношения (8.2.8) и (8.2.9)). Следовательно, наилучшей несмещенной линейной оценкой 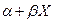 будет
будет 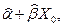 где
где 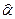 и
и 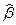 - параметры, полученные методом наименьших квадратов. С помощью формул (8.3.3) и (8.3.4) вычислим дисперсию
- параметры, полученные методом наименьших квадратов. С помощью формул (8.3.3) и (8.3.4) вычислим дисперсию 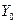 :
:
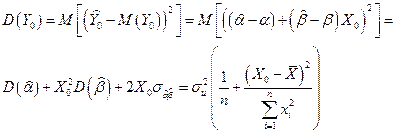
где 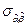 - ковариация между
- ковариация между 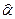 и
и 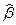 (см. (2.5.12)). Вывод: дисперсия прогноза возрастает по мере удаления рассматриваемой точки от среднего значения выборки, использованной для расчета параметров
(см. (2.5.12)). Вывод: дисперсия прогноза возрастает по мере удаления рассматриваемой точки от среднего значения выборки, использованной для расчета параметров 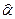 и
и 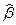 .
.
Дата добавления: 2019-07-26; просмотров: 495;
