Основные показатели оценки качества формы кривой выходного напряжения

Как было отмечено выше, кривая выходного напряжения инвертора содержит в своем составе кроме первой, так же и высшие гармоники, кото­рые вызывают дополнительные потери мощности, помехи и риск возникновения резонанс­ных процессов в цепях потребителей. Отметим, что множество современных приборов и устройств рассчитано именно на синусоидальное питающее напряжение, Для улучшения гармонического состава выходного напряжения инвертора на его выходе устанавливают выходные фильтры. Поэтому-то вопрос расчета выходных фильтров инверторов напряжения на заданныйкоэффициент гармоник очень важен в современной преобразовательной технике, так как является необходимым условием нор­мального функционирования приборов и ус­тройств потребителей, задавая ограничение по нелинейности выходного напряжения инвертора.

Рассмотрим основные показатели оценка качества формы кривой выходного напряжения.

Качество выходного напряжения принято оценивать следующими интегральными критериями:

Коэффициент несинусоидальности формы кривой выходного напряжения, k_н:

k_н=U₁/U, (32)

где: U₁ – действующее значение 1-ой гармоники напряжения;

U– действующее значение напряжения с учетом всех гармоник.

Коэффициент гармоник (или коэффициент искажения синусоидальности кривой напряжения), k_Г – это отношение действующего значения напряжения всех высших гармоник к действующему значению напряжению первой гармоники:

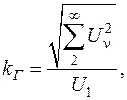(33)

где ν – номер гармоники;

U_ν – действующее значение ν – ой гармоники напряжения.

Для cинусоидального напряжения k_г=0.

Коэффициент несинусоидальности можно определить через коэффициент гармоник:

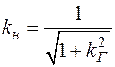. (34)

Для сравнительной оценки качества напряжения выходе инвертора удобно пользоваться коэффициентом режекции гармоники.

Коэффициент режекции гармоники, k_N – отношение действующего значения первой гармоники напряжения к первой учитываемой низшей из высших гармонических составляющих, умноженное на квадрат номера учитываемой гармоники:

k_N=(U₁/Uν )•ν ² . (35)

Для синусоидального напряжения коэффициент режекции k_N=∞.

Используя коэффициент режекции гармоники несинусоидального периодического напряжения, подведенного ко входу фильтра, можно

определить приблизительное значение требуемого произведения индуктивности на емкость однозвенного фильтра при заданном коэффициенте гармоник на выходе фильтра с помощью соотношения:

ω²LC=(1+k_г.выхk_N/ν ²)/(1+k_г.выхk_N), (36)

где k_г.вых– требуемое значение коэффициента гармоник на выходе фильтра.

ω =2πf– угловая частота выходного напряжения инвертора.

L, C– индуктивность и емкость выходного фильтра, соответственно.

Для двух сравниваемых двух форм напряжений при одинаковом качестве напряжения на выходе фильтра отношение 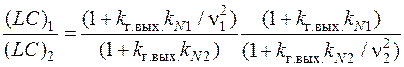(37):

(37)

позволяет оценить относительные затраты индуктивности и емкости однозвенного фильтра.

Пример: Даны два напряжения, подведенные ко входу фильтра и содержащие основную гармонику и высшую гармонику:

u₁=sinωt+(1/3) sin3ωt;

u₂= sinωt+(1/3) sin11ωt.

Требуемый коэффициент гармоник на выходе сглаживающего фильтра k_г.вых=0,1.

Сравним эти напряжения по критерию минимальных затрат индуктивности и емкости однозвенного L-C фильтра.

Решение:

Оценим эти напряжения путем сравнения коэффициентов гармоник их. Поскольку амплитуды основных и высших гармоник этих напряжений одинаковы, то и коэффициенты гармоник этих напряжений тоже одинаковы:

k_г1= k_г2=1/3=0,33.

Таким образом, различие между качеством напряжений установить не удается. Оценим эти напряжения с помощью коэффициента режекции гармоники. Используя соотношение (37) и учитывая, что коэффициент гармоник на выходе фильтра k_г.вых.=0,1, получим:

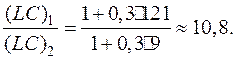
Т.е. в случае использования напряжения U₂, в составе которого находится 11-ая гармоника, требуемое произведение индуктивности на емкость однозвенного фильтра в 10 раз меньше, чем для напряжения U₁, в составе которого находится 3-ья гармоника._.

Ранее было установлено, что амплитуда любой гармоники выходного напряжения, содержащего один импульс на интервале полуволны, при широтном способе регулирования величины этого напряжения (смотри рисунок 5,д) определяется по формуле (4):

U_mν=[4U_d/(νπ)]sin(νγπ/2),

где U_d -среднее значение величины входного напряжения;

ν -номер гармоники;

γ- коэффициент скважности.

При широтно - импульсном регулирование величины выходного напряжения инвертора каждая полуволны этого напряжения содержит несколько прямоугольных импульсов, скважность которых γ регулируется в пределах от 0 до 1. Отметим, что частота следования этих прямоугольных импульсов напряжения равна несущей частоте, f_н.

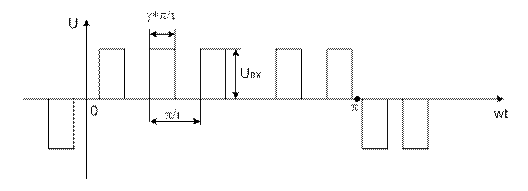
Рисунок 15. Однополярная форма кривой выходного напряжения при ШИР модуляции

U_d – уровень амплитуды импульса;

ν = 1;3;5;… порядковый номер гармоник;

i – число импульсов, формируемых интервале одной полуволны выходного напряжения;

γ- коэффициент скважности импульсов.

Период следования прямоугольных импульсов напряжения, Т^´=π/i.

Амплитуда ν –ой гармоники выходного напряжения (U_mν) с однополярной ШИМ по прямоугольному синусу (смотри рисунок 15), определяется по формуле:

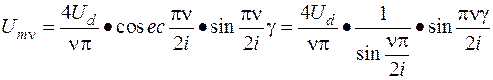(38)

Действующие значения напряжения переменного тока

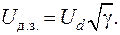(39)

Коэффициент гармоник формы напряжения, k_г, (для прямоугольного синуса)

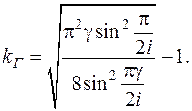(40)

Гармонический состав тока нагрузки

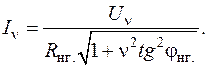(41)

Гармонический состав выходного напряжения с однополярной ШИМ и паузой между импульсами полуволн, равной 30⁰ , не содержит 3-ью и кратные ей гармоники.

Амплитуда любой высшей гармоники напряжения для этой формы выходного напряжения при регулировании коэффициента скважности γ в диапазоне от 0 до 1определяется по формуле

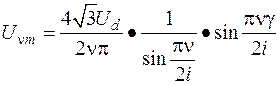(42)

Вопросы для самоконтроля:

1. Дайте определение понятию «коэффициент гармоник».

2. Дайте определение понятию «несинусоидальность формы кривой».

3. Дайте определение понятию «коэффициент режекции».