Графическое изображение статистического распределения
Статистическое распределение изображается графически (для наглядности) в виде так называемых полигона и гистограммы. Полигон, как правило, служит для изображения дискретного (т. е. варианты отличаются на постоянную величину) статистического ряда.
Полигоном частот называют ломаную, отрезки которой соединяют точки с координатами 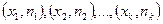 ; полигоном частостей - с координатами
; полигоном частостей - с координатами 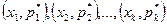 .
.
Варианты ( 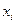 ) откладываются на оси абсцисс, а частоты и, соответственно, частости - на оси ординат.
) откладываются на оси абсцисс, а частоты и, соответственно, частости - на оси ординат.
Для непрерывно распределенного признака (т.е. варианты могут отличаться один от другого на сколь угодно малую величину) можно построить полигон частот, взяв середины интервалов в качестве значений 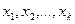 . Более употребительна так называемая гистограмма.
. Более употребительна так называемая гистограмма.
Гистограммой частот (частостей) называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению 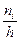 - плотность частоты. Отношения
- плотность частоты. Отношения 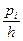 и
и 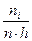 также являются плотностью частоты.
также являются плотностью частоты.
Очевидно, площадь гистограммы частот равна объему выборки, а площадь гистограммы частостей равна единице.
Пример 8.3. Построить полигон частостей для примера 8.1.
Решение:
Статистический ряд распределения данной задачи имеет вид
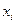
| ||||||
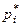
| 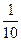
| 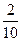
| 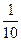
| 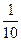
| 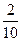
| 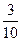
|
Отложив по оси х значения 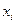 , а по оси у -
, а по оси у - 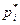 , построим полигон частостей (рис.8.2).
, построим полигон частостей (рис.8.2).
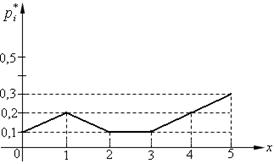
Рис. 8.2.
Заметим, что 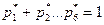 .
.
Как видно, полигон частостей является статистическим аналогом многоугольника распределения.
Пример 8.4.Измерили рост (с точностью до см) 30 наудачу отобранных студентов. Результаты измерений таковы:
178, 160, 154, 183, 155, 153, 167, 186, 163, 155,
157, 175, 170, 166, 159, 173, 182, 167, 171, 169,
178, 165, 156, 179, 158, 171, 175, 173, 164, 172.
Построить: а) интервальный статистический ряд; б) используя результаты построить гистограмму частостей.
Решение:
а) Для удобства проранжируем полученные данные:
153, 154, 155, 155, 156, 157, 158, 159, 160, 163,
164, 165, 166, 167, 167, 169, 170, 171, 171, 172,
173, 173, 175, 175, 178, 179, 179, 182, 183, 186.
Отметим, что X - рост студента - непрерывная случайная величина. При более точном измерении роста значения случайной величины X обычно не повторяются (вероятность наличия на Земле двух человек, рост которых равен, скажем 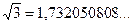 метров, равна нулю!).
метров, равна нулю!).
Как видим, 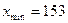 ,
, 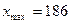 . По формуле Стерджеса, при
. По формуле Стерджеса, при 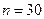 , находим длину частичного интервала
, находим длину частичного интервала
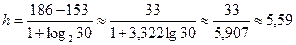
Примем 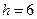 . Тогда
. Тогда 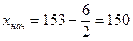 . Исходные данные разбиваем на 6 (
. Исходные данные разбиваем на 6 ( 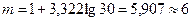 ) интервалов: [150, 156), [156, 162), [162, 168), [168, 174), [174, 180), [180, 186).
) интервалов: [150, 156), [156, 162), [162, 168), [168, 174), [174, 180), [180, 186).
Подсчитав число студентов ( 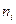 ) попавших в каждый из полученных промежутков, получим интервальный статистический ряд:
) попавших в каждый из полученных промежутков, получим интервальный статистический ряд:
| Рост | [150,156) | [156,162) | [162,168) | [168,174) | [174, 180) | [180, 186) |
| Частота | ||||||
| Частость | 0,13 | 0,17 | 0,20 | 0,23 | 0,07 | 0,10 |
б) Длина интервала равна 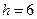 . Находим высоты
. Находим высоты 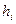 прямоугольников:
прямоугольников:
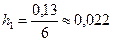 ,
, 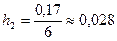 ,
, 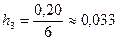 ,
, 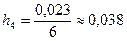 ,
, 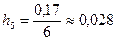 ,
, 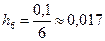 .
.
Построим гистограмму частостей (рис. 8.3).
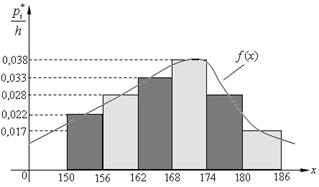
Рис. 8.3.
Гистограмма частот является статистическим аналогом дифференциала функции распределения (плотности) 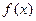 случайной величины X. Сумма площадей прямоугольников равна 1.
случайной величины X. Сумма площадей прямоугольников равна 1.
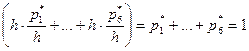 ,
,
что соответствует условию 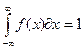 для плотности вероятностей
для плотности вероятностей 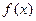 . На рис. 8.3 показана и плотность вероятностей
. На рис. 8.3 показана и плотность вероятностей 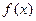 .
.
Если соединить середины верхних оснований прямоугольников отрезками прямой, то получим полигон того же распределения.
Дата добавления: 2017-03-29; просмотров: 321;
