Неравенство Чебышева
Рассмотрим ряд утверждений и теорем из большой группы так называемых предельных теорем теории вероятностей, устанавливающих связь между теоретическими и экспериментальными характеристиками случайных величин при большом числе испытаний над ними. Они составляют основу математической статистики. Предельные теоремы условно делят на две группы. Первая группа теорем, называемая законом больших чисел, устанавливает устойчивость средних значений, т.е. при большом числе испытаний их средний результат перестает быть случайным и может быть предсказан с достаточной точностью. Вторая группа теорем, называемая центральной предельной, устанавливает условия, при которых закон распределения суммы большого числа случайных величин неограниченно приближается к нормальному.
В начале рассмотрим неравенство Чебышева, которое можно использовать для: а) грубой оценки вероятностей событий, связанных со случайными величинами, распределение которых неизвестно; б) доказательства ряда теорем закона больших чисел.
Теорема 7.1. Если случайная величина X имеет математическое ожидание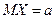 
и дисперсию DX, то для любого 
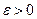справедливо неравенство Чебышева
 .
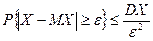| (7.1) |
Отметим, что неравенство Чебышева можно записать в другой форме:
 .
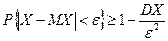| (7.2) |
В форме (7.2) оно устанавливает нижнюю границу вероятности события, а в форме (7.1) – верхнюю.
Неравенство Чебышева справедливо для любых случайных величин. В частности, для случайной величины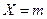 
, имеющей биноминальное распределение, с математическим ожиданием 
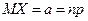и дисперсией 
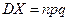, оно принимает вид
 ,
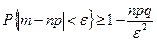| (7.3) |
для частости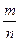 
или 
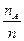события в n независимых испытаниях, в каждом из которых оно может произойти с вероятностью 
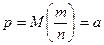, дисперсия которых 
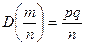, неравенство Чебышева имеет вид
 .
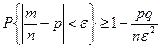| (7.4) |
Оценку вероятности попадания случайной величины Х в промежуток 
дает неравенство Маркова.
Теорема 7.2 (Неравенство Маркова). Для любой неотрицательной случайной величины Х, имеющей математическое ожидание MX и 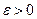, справедливо неравенство:
 .
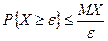| (7.5) |
Неравенство (7.5) можно переписать в виде
 .
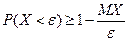| (7.6) |
Пример 7.1. Оценить с помощью неравенства Чебышева вероятность того, что отклонение случайной величины Х от своего математического ожидания будет меньше трех средне квадратических отклонений, т.е. меньше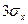 
.
Решение:
Полагая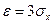 
в формуле (7.2), получаем
.
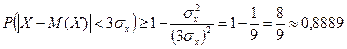Эта оценка называется правилом трех сигм.
Теорема Чебышева
Основное утверждение закона больших чисел содержится в теореме Чебышева. В ней и других теоремах закона больших чисел используется понятие «сходимости случайных величин по вероятности».
Случайные величины 
сходятся по вероятности к величине А (случайной или неслучайной), если для любого 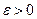вероятность события 
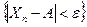при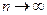 
стремится к единице, т.е.
(или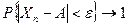 
). Сходимость по вероятности символически записывают так:
.
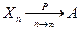Следует отметить, что сходимость по вероятности требует, чтобы неравенство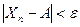 
выполнялось для подавляющего числа членов последовательности (в математическом анализе - для всех n > N, где N - некоторое число), а при 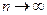практически все члены последовательности должны попасть в ε-окрестность А.
Теорема 7.3 (Закон больших чисел в форме П.Л. Чебышева). Если случайные величины 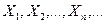независимы и существует такое число С>0, что 
, 
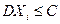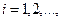то для любого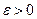
 ,
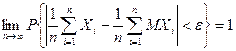| (7.7) |
т.е. среднее арифметическое этих случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий:
.
Доказательство. Так как 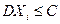, 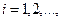то
.
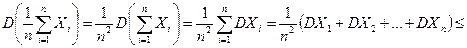
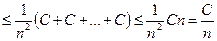Тогда, применяя к случайной величине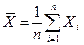 
неравенство Чебышева (7.2) имеем
 .
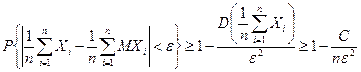| (7.8) |
Переходя к пределу при 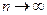и учитывая, что вероятность любого события не превышает 1, получаем .
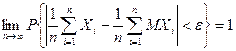Следствие.Если случайные величины 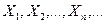независимы и одинаково распределены, 
, 
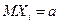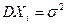, то для любого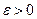
 ,
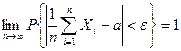| (7.9) |
т.е. среднее арифметическое случайных величин сходится по вероятности к математическому ожиданию а:
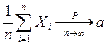
Доказательство. Так как
,
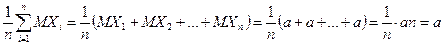а дисперсии случайных величин 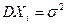, т.е ограничены, то применив теорему Чебышева (7.7), получим утверждение (7.9).
Следствие теоремы Чебышева обосновывает принцип «среднего арифметического» случайных величин Хi, постоянно используемый на практике. Так, пусть произведено n независимых измерений некоторой величины, истинное значение которой а (оно неизвестно). Результат каждого измерения есть случайная величина Хi. Согласно следствию, в качестве приближенного значения величины а можно взять среднее арифметическое результатов измерений:
.
Равенство тем точнее, чем больше n.
На теореме Чебышева основан также широко применяемый в статистике выборочный метод, суть которого в том, что о качестве большого количества однородного материала можно судить по небольшой его пробе.
Теорема Чебышева подтверждает связь между случайностью и необходимостью: среднее значение случайной величины 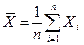практически не отличается от неслучайной величины 
.
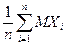Теорема Бернулли
Теорема Бернулли исторически является первой и наиболее простой формой закона больших чисел. Она теоретически обосновывает свойство устойчивости относительной частоты.
Теорема 7.4 (Закон больших чисел в форме Я. Бернулли). Если вероятность появления события А в одном испытании равна р, число наступления этого события при n независимых испытаниях равно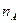 
, то для любого числа 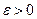имеет место равенство
 ,
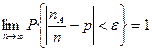| (7.10) |
т.е относительная частота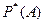 
события А сходится по вероятности к вероятности р события А: 
.
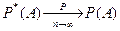Доказательство. Введем случайные величины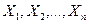 
следующим образом: 
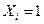, если в i-м испытании появилось событие А, а если не появилось, то 
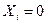. Тогда число А (число успехов) можно представить в виде
.
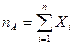Математическое ожидание и дисперсия случайных величин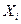 
равны: 
, 
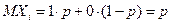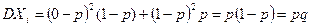. Закон распределения случайных величин Xi имеет вид
| Хi | ||
| Р |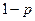 
| р |
при любом i. Таким образом, случайные величины Xi независимы, их дисперсии ограничены одним и тем же числом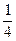 
, так как
.
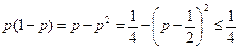Поэтому к этим случайным величинам можно применить теорему Чебышева
.
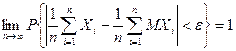Но
, 
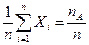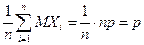
Следовательно,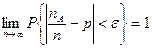 
.
Теорема Бернулли теоретически обосновывает возможность приближенного вычисления вероятности события с помощью его относительной частоты. Так, например, за вероятность рождения девочки можно взять относительную частоту этого события, которая, согласно статистическим данным, приближенно равна 0,485.
Неравенство Чебышева (7.2) для случайных величин
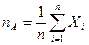
принимает вид
 .
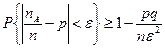| (7.11) |
Обобщением теоремы Бернулли на случай, когда вероятности pi появления события А в каждом из n испытаний различны, является теорема Пуассона:
 ,
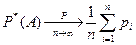| (7.12) |
где pi - вероятность события А в i-м испытании.
Пример 7.2. Вероятность наличия опечатки на одной странице рукописи равна 0,2. Оценить вероятность того, что в рукописи, содержащей 400 страниц, частость появления опечатки отличается от соответствующей вероятности по модулю меньше, чем 0,05.
Решение:
Воспользуемся формулой (7.11). В данном случае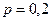 
, 
, 
, 
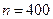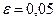. Имеем 
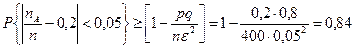, т.е. 
.
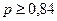Дата добавления: 2017-03-29; просмотров: 264;