Центральная предельная теорема
Центральная предельная теорема представляет собой вторую группу предельных теорем, которые устанавливают связь между законом распределения суммы случайной величины и его предельной формой - нормальным законом распределения.
Сформулируем центральную предельную теорему для случая, когда члены суммы имеют одинаковое распределение. Эта теорема чаще других используется на практике. В математической статистике выборочные случайные величины имеют одинаковые распределения, так как получены из одной и той же генеральной совокупности.
Теорема 7.5. Пусть случайные величины 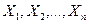 независимы, одинаково распределены, имеют конечные математическое ожидание
независимы, одинаково распределены, имеют конечные математическое ожидание 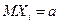 и дисперсию
и дисперсию 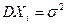 ,
, 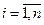 . Тогда функция распределения центрированной и нормированной суммы этих случайных величин стремится при
. Тогда функция распределения центрированной и нормированной суммы этих случайных величин стремится при 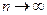 к функции распределения стандартной нормальной случайной величины:
к функции распределения стандартной нормальной случайной величины:
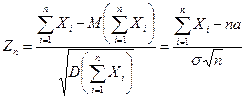 , ,
| (7.13) |
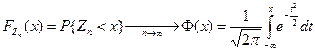
Из соотношения (7.13) следует, что при достаточно большом n сумма Zn приближенно распределена по нормальному закону: 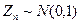 . Это означает, что сумма
. Это означает, что сумма 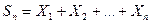 приближенно распределена по нормальному закону:
приближенно распределена по нормальному закону: 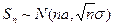 . Говорят, что при
. Говорят, что при 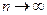 случайная величина
случайная величина  асимптотически нормальна.
асимптотически нормальна.
Напомним, что:
1. Случайная величина X называется центрированной и нормированной (т.е. стандартной), если MX = 0, a DX = 1.
2. Если случайные величины 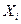 ,
, 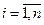 независимы,
независимы, 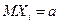 ,
, 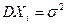 , то
, то
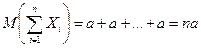 ,
,
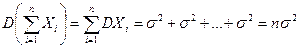 .
.
3. 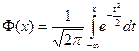 - функция Лапласа,
- функция Лапласа, 
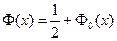 , где
, где 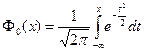 - нормированная функция Лапласа.
- нормированная функция Лапласа.
Формула (7.13) позволяет при больших n вычислять вероятности различных событий, связанных с суммами случайных величин. Так, перейдя от случайной величины
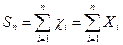
к стандартной случайной величине, получим:
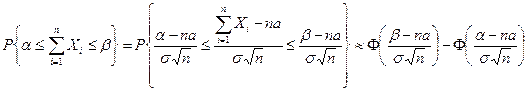 ,
,
Или
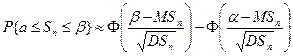 . .
| (7.14) |
Формула (7.14) определяет вероятность того, что сумма нескольких случайных величин окажется в заданных пределах. Часто центральную предельную теорему используют, если n>10.
Пример 7.3.Независимые случайные величины 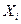 распределены равномерно на отрезке
распределены равномерно на отрезке 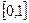 . Найти закон распределения случайной величины
. Найти закон распределения случайной величины 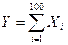 , а также вероятность того, что
, а также вероятность того, что 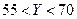 .
.
Решение:
Условия центральной предельной теоремы соблюдаются, поэтому случайная величина Y имеет приближенно плотность распределения
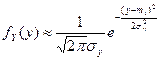 .
.
По известным формулам для математического ожидания и дисперсии в случае равномерного распределения находим:
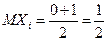 ,
, 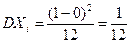 ,
, 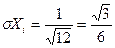 .
.
Тогда
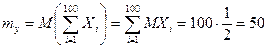 ,
,
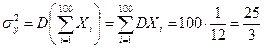 ,
, 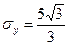
Поэтому
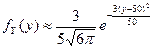 .
.
Используя формулу (7.14), находим
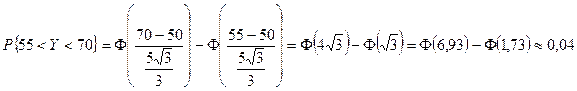 ,
,
т.е. 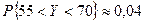 .
.
Дата добавления: 2017-03-29; просмотров: 264;
