Проектирование механизма изменения вылета стрелы

Изменение вылета стрелы обеспечивает горизонтальное перемещение поднятого груза в определенных пределах.

Изменение вылета стреловых кранов и специальных крановых установок производят изменением наклона стрелы в вертикальной плоскости.

Механизмы изменения вылета стрелы могут иметь как гибкую (рис. 136), так и жесткую связь привода со стрелой (рис. 138).

Для расчета механизма изменения вылета стрелы должно быть установлено: схема механизма с необходимыми параметрами, которые в процессе проектирования будут уточняться (рис. 136); грузоподъемность Q; вес стрелы G_c; натяжение каната S механизма подъема груза 5; скорость подъема (опускания) стрелы 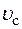; режим работы крана.

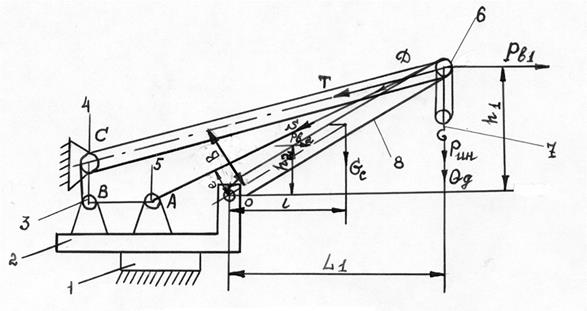
Рис. 136. Схема механизма изменения вылета стрелы с гибкой связью

Изменение угла наклона стрелы 8 осуществляется стреловой лебедкой 3 с помощью стрелового полиспаста (блоки 4, 6 и канат).

По конструкции механизмы изменения вылета с канатным полиспастом аналогичны механизмам подъема груза. Они включают двигатель, редуктор, лебедку, тормоза, стреловой полиспаст.

Для изменения вылета к стреле необходимо приложить силу Т

(рис. 136), которую определяют из уравнения моментов всех сил, действующих на стрелу при ее проекции L₁ , относительно оси её вращения (·)О.

,

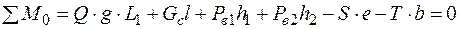где 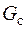- вес стрелы;

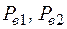- ветровые нагрузки на груз и стрелу соответственно;

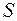- натяжение каната механизма подъема груза;

e, b, h₁, h₂, L₁- плечи действия сил .

Из данного выражения следует

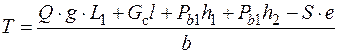. (150)

Увеличение плеч b и e , относительно оси поворота стрелы, приводит к уменьшению требуемой силы T. Центробежную силу и силу инерции груза в данном случае не учитывают.

Максимальное натяжение каната на барабане определяют по выражению

.

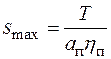При изменении вылета от максимального до минимального значений расстояния между осями обоймы полиспаста уменьшится на величину 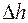. Тогда средняя скорость навивки каната на барабан u_кбудет равна

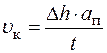, (149)

где 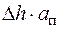-длина каната, навиваемого на барабан;

t - время изменения вылета.

По силе натяжения каната S_max механизма изменения вылета, определенной для крайних и нескольких промежуточных положении стрелы, строится диаграмма загрузки привода, по ней можно определить среднеквадратический момент и требуемую мощность двигателя.

Наибольшая мощность N_max (кВт) при установившемся движении, соответствующая максимальному вылету при силе S_max, равна

.

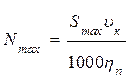Далее расчеты аналогичны расчетам механизма подъема груза (подр. 8.6).

Обычно натяжение каната механизма изменения вылета стрелы имеет максимальное значение в крайнем нижнем положении стрелы, постепенно уменьшаясь по мере её подъема. Но так как грузоподъемность зависит от вылета стрелы, то необходимо провести расчеты силы T натяжения каната для нескольких значений вылета стрелы и найти её максимальное значение.

Из данных рассуждений и анализа выражения (148) следует, что величина силы Т зависит не только от вылета стрелы, но и от компоновки механизмов подъема и опускания груза и стрелы.

Так как потребное усилие Т для подъема стрелы зависит от компоновки стрелы 8 (рис. 137), грузовой 5 и стреловой 3 лебедок и блоков 4, 6 стрелового полиспаста (положения точек О, А, В, С, Д), то, очевидно, можно сформулировать и решить задачу поиска рациональных параметров компоновки стрелы, механизмов подъема и опускания груза и стрелы.

Найти координаты точек О, А, В, С, Д установки стрелы, грузовой и стреловой лебедок и блоков стрелового полиспаста из области их возможных значений, при которых потребное усилие T для подъема стрелы будет минимальным. Геометрия компоновки элементов поворотной части представлена на рисунке 137.

Математически данную задачу можно сформулировать следующим образом:

;

;

.

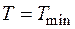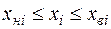Здесь - ограничения на координаты положения i -й точки установки элементов поворотной части.

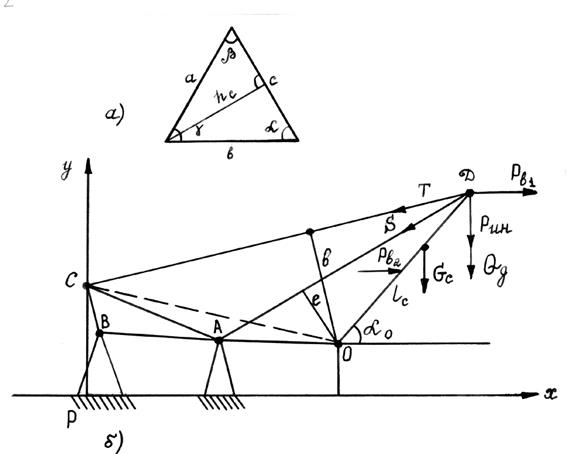
Рис. 137. Геометрия компоновки элементов поворотной части крана

Для решения данной задачи необходима разработка математической модели, выражающей усилие T в функции от нагрузок и координат положения элементов поворотной части.

При разработке математической модели будем полагать, что известны координаты 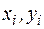точек О, A, В, C, D и соответствующие нагрузки на поворотную часть (рис. 137).

Данная задача решается в следующей последовательности при фиксированном угле подъема стрелы:

1.Находятся длины сторон l_ij треугольников по известным координатам их вершин

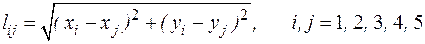
2. Определяются необходимые углы 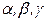соответствующих треугольников (рис. 137, а)

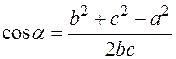и т.п.

3. Находятся плечи действия сил 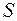и 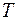, используя соотношения типа

.

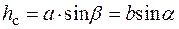4. По выражению (150) вычисляется сила T.

Для решения задачи выбора рациональных параметров механизма целесообразно использовать один из методов поисковой оптимизации, основанный на выборе направлений поиска минимума силы Т по результатам последовательных вычислений целевой функции. Алгоритм поиска рациональных параметров механизма представляет собой многошаговое решение задачи динамического программирования методом наискорейшего спуска [25]. Идея метода оптимизации заключается в следующем:

1. Вычисляется значение Т₀ для начальной точки поиска (при начальных значениях параметров ). Эта точка соответствует наихудшему решению.

2. Даются приращения каждому параметру 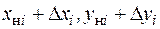и вычисляются значения T_i .

3. Вычисляется градиент 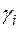для каждого параметра

.

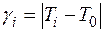4. Находится градиент 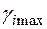, свидетельствующий, что изменение параметра i , соответствующего 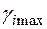, позволяет достигнуть мень­шего значения критерия оптимальности T^* , чем изменение других параметров. Рациональное значение параметров на данном шаге поиска будет .

5. Вычисления по пунктам 2-4 повторяются с учетом найденных T^* и .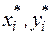

6. Поиск прекращается после анализа значений критерия Т во всей области изменения параметров.

В результате решения задачи находятся Т_min и соответствующие ему рациональные значения параметров компоновки элементов вращающейся части крана x_iрац и y_iрац.

При жесткой подвеске стрелы крана (рис. 138) в качестве механизма ее подъема обычно применяется гидродомкрат или, реже, винтовой домкрат.

Принципиальная схема механизма (рис. 138) аналогично во многом схеме механизма подъема направляющей пусковой установки (подр. 8.4), но имеет ряд особенностей, связанных с видом и распределением нагрузок.

В данном случае при проектировании необходимо произвести климатический и силовой расчеты механизма.

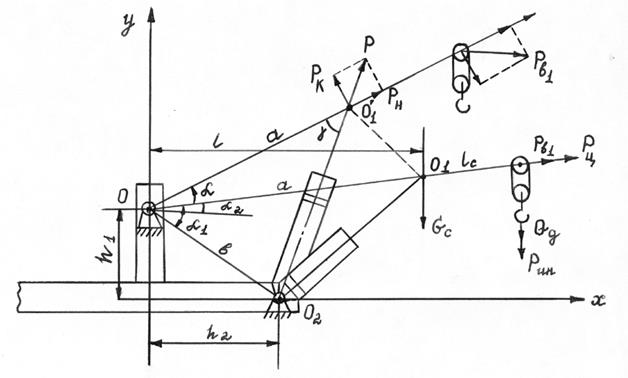
Рис. 138. Принципиальная схема механизма изменения