Расчет рамы транспортной машины методом конечных элементов
Типовая опорная рама для размещения элементов специальной части ТМ (ТЗМ, ПУ) представляет собой сварную конструкцию из специальных профилей (рис. 130),основу которой составляют левая и правая продольные балки 1, соединенные между собой поперечными связями 2, ребрами. 3, 5 и накладками 4, 7. Ниши 8, 9, 10 предназначены для монтажа элементов специальной части. Все балки и связи свариваются из гнутых профилей и имеют коробчатое сечение.
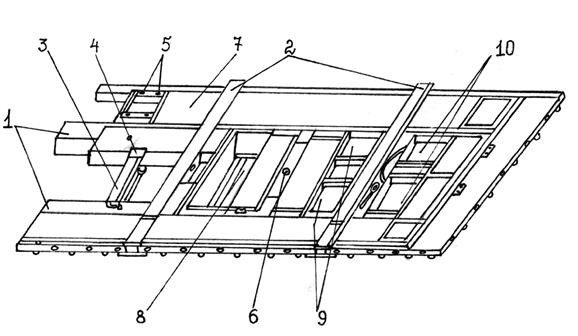
Рис. 130. Опорная рама
Опорная рама крепится шарнирно в трех точках к раме базового шасси. Такое крепление значительно снижает передачу крутящих моментов на опорную раму при движении АНО. Конструкция опорной рамы может быть представлена стержневой КЭ-моделью в виде некоторой совокупности прямолинейных одномерных КЭ-стержней постоянного поперечного сечения. Число КЭ зависит от особенностей конструктивно-силовой схемы и характера действующих нагрузок.
Опорная рама выполнена конструктивно симметричной относительно продольной оси, при развеске ТМ достигается и симметрия нагрузок от веса элементов оборудования. В силу симметрии конструкции и внешней нагрузки проведем расчет правой половины опорной рамы.
В качестве расчетного случая примем транспортирование изделий с максимальной скоростью. В этом случае опорная рама, плоская в геометрическом отношении, будет нагружена силовыми факторами, перпендикулярными плоскости рамы, динамические нагрузки учтем с помощью коэффициента кд. Элементы рамы будут нагружены изгибающими Муи крутящими Мк моментами и вертикальной поперечной силой R, действующими в плоскости, перпендикулярной плоскости рамы.
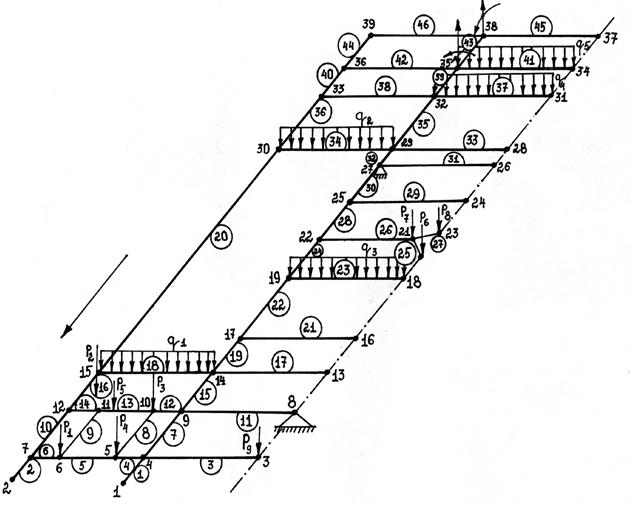
Рис.131. КЭ-модель опорной рамы
Расчетная схема правой части рамы с нумерацией узлов и КЭс нагрузками в плоскости, перпендикулярной плоскости рамы, представлена на рис. 131.
На опорную раму действуют следующие нагрузки:
Р1, Р2, Р3, Р4 - вес агрегата питания;
Р5- вес топливного бака агрегата питания;
Р6, Р7, Р8- вес лотка с досылателем;
Р9- вес крановой установки;
q1, q2-распределенные нагрузки от веса ложементов и снарядов;
q3- распределенная нагрузка от веса элементов электрооборудования;
q4, q5-распределенные нагрузки от веса элементов ЗИП.
Учитывая характер нагружения, опорную раму, представленную на рисунке 131, разбиваем на 46 стержневых КЭ, в которых будут действовать деформации изгиба, кручения и вертикальная поперечная сила в одной плоскости, перпендикулярной к плоскости рамы. Расчетная схема содержит 39 узлов, неизвестными в которых будут три перемещения: поступательное и два угловых (показаны только в узлах 35 и 38), положительные направления которых представлены на рисунке 132.
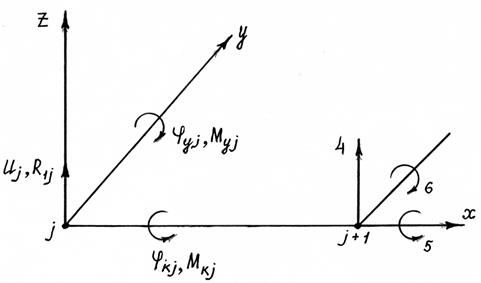
Рис.132. Положительные направления узловых перемещений и сил для стержневого КЭ при деформационных воздействиях в вертикальной плоскости
Вектор перемещений j-го узла е-го КЭ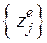 
в ЛСК при деформационных воздействиях в вертикальной плоскости (рис. 132) составим в виде
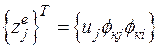, (138)
где uj – поступательное перемещение узла j по направлению z;
jкj, jуj – повороты узла j относительно осей х и y.
Перемещениям соответствуют обобщенные реакции
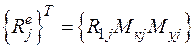. (139)
Матрица жесткости стержневого КЭ [Ке]для плоской модели при нагрузке в вертикальной плоскости представим в виде
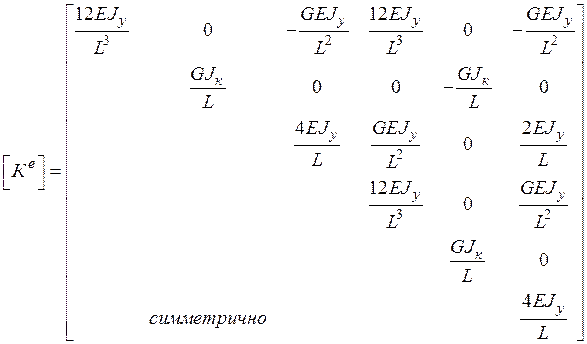. (140)
Здесь Е - модуль упругости первого рода; A - площадь поперечного сечения стержня; L - длина стержня; Jу - осевой момент инерции сечения относительно оси y; G - модуль упругости второго рода; Jк - полярный момент инерции сечения (при кручении).
В рассматриваемом случае вектор узловых усилий, эквивалентный внешней распределенной нагрузке, приложенной к стержневому КЭ, имеет вид
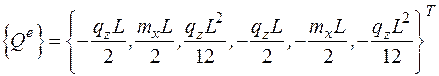. (141)
Здесь q, mx - равномерно распределенные нагрузки вдоль соответствующих осей.
Алгоритм расчета плоской стержневой модели включает следующие модули.
Модуль 1. Подготовка исходных данных.
Основные параметры КЭ - модели: число узлов М, число жестких опор Ма, число КЭ N; число нагруженных KЭ Np.
Массивы информации, описывающие узловые элементы:
массив координат узлов в ГСК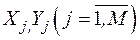 
;
массив жестких опор, содержащий порядковый номер узла j, некоторые компоненты i вектора перемещений которого равны нулю; элемент массива i j содержит нуль, если i -я компонента вектора перемещений неизвестна, и единицу, если эта компонента равна нулю;
массив узловых нагрузок, в j-й строке которого размещаются: порядковый номер нагруженного узла и действующие в нем сосредоточенные силы и изгибающие моменты.
Массивы информации об КЭ:
массив топологии, в е-й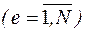 
строке которого последовательно размещаются номера узлов, с которыми связан этот КЭ и номер (признак) типа КЭ;
массив характеристик КЭ (А, Jу, Jк, Е, G);
массив нагрузок, в i -й строке которого последовательно размещаются: номер е КЭ, к которому приложены внешние нагрузки, а также их значения.
Модуль 2. Формирование матрицы индексов.
Матрица индексов размером М ´ lП содержит глобальную нумерацию неизвестных КЭ - модели от 1 до (М× lП). Здесь lП - число узловых перемещений (степеней свободы) узла. Пoрядок автоматического формирования матрицы индексов изложен в учебном пособии [14].
Модуль 3. Расчет MЖ стержневого КЭ в ЛСК.
В алгоритме реализуется поэлементный подход, позволяющий производить последовательную обработку КЭ, что обеспечивает экономию памяти ЭВМ. Вычисляются коэффициенты МЖ е-го КЭ, при этом его длина L определяется по координатам Xj, Yj начального узла j и Xj+1, Yj+1 конечного узла j+1, заданным в исходных данных
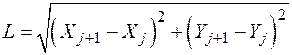(142)
Рассчитываются направляющие косинусы между осями ГСК и ЛСК для е-го КЭ
, 
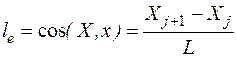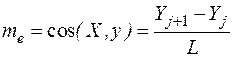. (143)
Модуль 4. Преобразование МЖ [Ke] и вектора распределенной нагрузки {Qe} e-го КЭ в ГСК.
Для этого формируется матрица [T0], которая в данном случае имеет вид
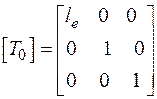, (144)
а полная матрица преобразования координат [T]
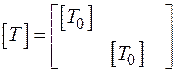(145)
МЖ и вектор распределенной нагрузки преобразуются в ГСК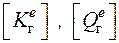 
по выражениям
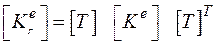, (146)
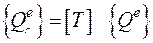. (147)
Модуль 5. Формирование глобальной МЖ и глобального вектора внешней нагрузки.
Глобальная МЖ конструкции [K] формируется путем суммирования из МЖ [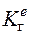 
] соединяющихся в узлах в соответствии с глобальной нумерацией неизвестных, приведенной в матрице индексов [14, 32].
Вектор внешних суммарных узловых сил {P}образуется расстановкой в соответствии с глобальной нумерацией неизвестных сосредоточенных нагрузок, взятых из исходных данных, и суммированием элементов векторов распределенной нагрузки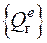 
для КЭ, соединяющихся в узлах.
Модуль 6. Учет кинематических закреплений конструкции.
Информация для учета кинематических закреплений конструкции содержится в исходных данных (в массиве жестких опор). Если i-я компонента вектора перемещений по условиям закрепления конструкции равна нулю, то общее число неизвестных уменьшается на единицу, а в матрице [K] и в векторе {P} исключаются соответствующие строки и столбцы. Число неизвестных (уравнений) в системе уменьшается и будет составлять{Z*}.
Модуль 7. Решение системы алгебраических уравнений.
В результате решения системы уравнений находится вектор неизвестных перемещений {Z*} узлов конструкции в ГСК.
Модуль 8. Расчет внутренних силовых факторов.
В векторе {Z*} с помощью матрицы индексов выделяется вектор перемещений е -го КЭ в ГСК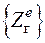 
, который преобразуется в ЛСК 
по выражению (142). Рассчитываются узловые силы е-го КЭ, для чего необходимо снова формировать MЖ е-го КЭ. Данные операции проводятся в цикле по всем КЭ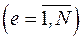 
. В результате расчета будут найдены узловые нагрузки 
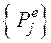для j -го узла
.
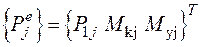По значениям внутренних силовых факторов для элементов рамы определенного типа устанавливают наиболее нагруженное (опасное) поперечное сечение. Для расчета на прочность необходимо выяснить наиболее напряженную точку в опасном сечении и вид напряженного состояния в этой точке для правильного составления условия прочности по методу допускаемых напряжений. Для прямоугольного поперечного сечения (рис. 133) в зависимости от соотношения сторон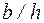 
и полученных соотношений между Mk и My наиболее напряженной может оказатьcя одна из трех точек: А, В или С. Для более напряженной точки вычисляется эквивалентное напряжение.
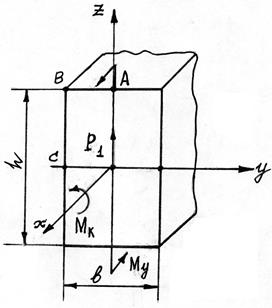
Рис. 133. Напряженное состояние сечения стержня
Модуль 9. Формирование результатов расчетов.
Результаты расчетов представляются в виде таблиц значений перемещений 
и нагрузок 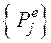в узлах.
При реализации разработанного алгоритма возможно проведение с помощью ЭВМ следующих исследований:
расчет НДС плоских стержневых конструкций при различных видах нагружения и условий закрепления, используя соответствующие МЖ КЭ;
выбор рациональных значений геометрических характеристик сечений стержней конструкции;
определение оптимальных соотношений между размерами элементов стержневой конструкции.
Глава 10
Дата добавления: 2019-04-03; просмотров: 347;