ВОПРОС. Как распределяются невязки fх и fу в приращения координат? 3 страница

Известны методы нивелирования поверхности параллельными ли-­
ниями, магистралями и по квадратам. Наиболее широкое распространение нашел последний способ особенно при планировочных работах на строительных площадках на открытой местности, со слабо выраженным рельефом. .

9.7.2. Нивелирование поверхности по квадратам начинают с разбив­ки на местности сетки квадратов с помощью теодолита и ленты. Сначала разбивают квадрат со сторонами 100-200 м и больше, после чего каждый из них разбивают на более мелкие квадраты со сторонами 10, 20 или 50м.

Точки закрепляют забитыми вровень с землей колыш­ками, а рядом забивают сторожок, на котором пишут номер точки.

9.7.3. Порядок нивелирования квадратов зависит от их размера и предельной длины визирного луча в 150 м. При размерах квадратов 100х100 м нивелируют каждый квадрат в отдельности. Нивелир устанав­ливают в центре квадрата и, приведя его в рабочее положение, берут отсчеты а₁, в₁, с₁, д₁ по рейке, последовательно установленной в каж­дой вершине квадрата. Затем нивелир переносят в центр следующего квадрата, приводят его в рабочее положение и берут отсчеты а₂, в₂, с₁₂, д₂ по рейке, установленной в вершинах. и так нивелируют все квадраты. В этом случае правильность отсчетов по рейкам контроли­руют по равенству отсчетов в₁ - а₁ = в₂ – а₂, где а₁, в₁ - отсчеты по рей­кам с первой станции; а₂, в₂ - отсчеты по рейкам на тех же верши­нах, но со второй станции. Допустимое расхождение ±20мм.

Если стороны квадратов 10 – 20 м, то с одной станции можно ни­велировать несколько квадратов. В этом случае вершины квадратов принимают связующими точками, которые образуют ход, нивелирование производится аналогично продольному нивелированию.

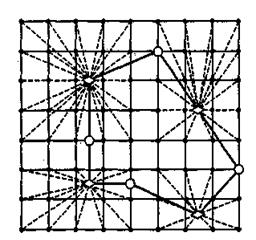
Рис.3.38. Схема нивелирова­ния по квадратам:

Для одной из вершин квадрата дается привязка к реперу государственного ни­велирования. Ситуацию при нивелировании по квадратам снимают спо­собом перпендикуляров от ближайших вершин квадратов.

9.7.4. Камеральные работы начинают с проверки результатов изме­рений. Вычисляют превышения и определяют фактическую невязку в нивелирном ходе. Сравнивают ее с допустимой, которую вычисляют по формуле

f_{h доп} = ± 4 √ К , где К - число станций хода.

Если полученная фактическая невязка меньше допустимой, то ее рас­пределяют поровну в превышения хода с обратным знаком. По исходной отметке и увязанным превышениям вычисляют отметки остальных вершин хода Н_111/4= H_1/5 + h. Затем вычисляют отметки остальных вершин квадратов через горизонт инструмента Н = ГИ -отсчет на точке.

Вычисления ведутся с точностью до 0,01м.

9.7.5. Для составления плана на чертежную бумагу наносится сетка квадратов в масштабе, выписываются отметки и наносится ситуа­ция. По отметкам вычерчиваются горизонтали. План вычерчивается в условных знаках для данного масштаба.

9.8. Поправка за кривизну Земли и рефракцию.

9.8.1. Поправка за кривизну Земли при определении высоты точки земной поверхности выражается формулой ρ = S² / 2 R,

где S - длина визирного луча от инструмента до рейки,

R - радиус Земли, равный 6371 км.

Как видно, поправка за кривизну Земли растет пропорциональ­но квадрату расстояния от инструмента до рейки. Например, при рас­стояниях равных 100, 200, 300, 1000 м ρ соответственно равно: 0,8, 3,1 , 7,1 и 7,8 мм.

9.8.2. Поправка за рефракцию q возникает из-за неравномерной плотности земной атмосферы. С увеличением высоты плотность умень­шается, поэтому луч визирования, преломившись в слоях земной ат­мосферы различной плотности, пойдет по кривой, обращенный вогну­тостью к поверхности Земли (рис. 3.39).

Поправка за рефракцию В₁В₂ при длине визирного луча прибли-­
зительно равна

q = 1/7 ρ = 1/14 S² / R.

Сумарная поправка в отсчете по рейке за кривизну Земли и рефракцию будет

f = ρ – q = S² / 2 R - 1/7 S² / 2R = 0.43 S² / R.

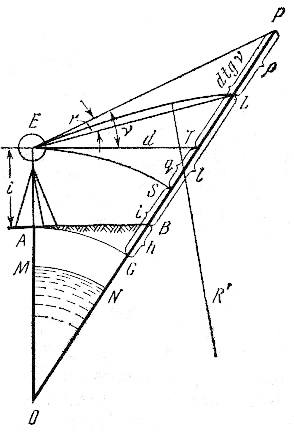
Рис.3.39. Поправка за рефракцию

9.8.3. Если учитывать влияния кривизны Земли. и рефракции при нивелировании (а это нужно делать, см. п.1.5.), то формулы превышений примут вид: h = i- (в - f) при нивелировании впе­ред, а при нивелировании из середины: h =(а – f₁) - (в – f₂) .

ВОПРОС. Объясните, почему при производстве нивелирования на станции инструмент устанавливают точно в середине между рейками на задней и передней точках? Выберите правильный ответ.

I. Исключения влияния ошибки за непараллельность визирной оси трубы и оси цилиндрического уровня (п. 9.8.5).

2. Для исключения влияния кривизны Земли и рефракции (9.8.6).

Выбранный Вами ответ проверьте.

Для приведения визирного луча в горизонтальное положение в
нивелире необходимо иметь уровень, с помощью которого и устанав-­
ливают визирную ось горизонтально. Если нивелир поставить в любой, точке между двумя пикетами, то в этой точке можно установить ось в горизонтальное положение. Следовательно, приведение луча в горизонтальное положение не зависит от положения точки, в которой ус­тановлен нивелир. Поэтому верным будет второй ответ. Вернитесь к формуле и подумайте, каковы будут величины поправок за кривизну Земли и рефракцию, если расстояния от нивелира до реек будут равны. Начертите чертеж.

9.8.5. Действительно, при нивелировании из середины расстояния от нивелира до реек будут равны, а, следовательно будут равны и поп­равки за влияние кривизны Земли и рефракцию. При раскрытии скобок они сократятся и формула примет обычный вид.

9.9. Тригонометрическое нивелирование.

9.9.1. Тригонометрическое нивелирование имеет целью создание высотной основы для топографических съемок и при решении различ­ных инженерных задач. Тригонометрическое нивелирование выполняется наклонным лучом визирования с помощью теодолита. Его достоинством является возможность передачи высотных отметок на большие расстояния.

9.9.2. Для определения превышения h между точками А и В (рис.3.40) в одной из точек А устанавливают теодолит-тахеометр, а в точке В рейку, наводят трубу на верх визирного знака /рейки/ и измеряют угол наклона υ.

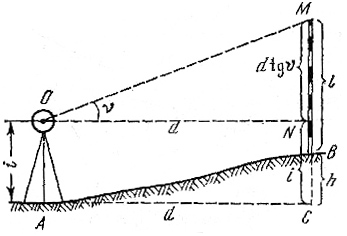
Рис. 3.40.Тригоноетрическое нивелирование

Если горизонтальное проложение линии АВ - d, высота инструмента и рейки соответственно i и l , то как следует из рисунка l + h = h´ + i или

h = h´ + i - l

Поскольку h´ = d tgυ

то превышение между точками А и В будет равно

h = d tgυ+ i - l

Эта формула получена без учета кривизны Земли и рефракции.

Поскольку превышения в тригонометрическом нивелировании вычисляют до 0,01м, а значение поправки за кривизну Земли и рефракцию f = 0,01 м при расстоянии между инструментом и рейкой в 300 м, то поправка вводится в превышения, определенные для расстояний свыше 300м.

ВОПРОС. Можно ли в формуле приравнять i и l ?

Выберите ответ и проверьте его.

1. Да, можно (п. 9.9.3.)

2. Нет, нельзя (п. 9.9.4)

Ответ 9.9.3. Действительно, если приравнять iиl, т.е. навести гори­зонтальную нить сетки нитей на отсчет по рейке, равный i, то iиl, в формуле сократятся и формула упростится и примет
h = d tgυ. Этот прием находит широкое применение при топогра-
фической съемках, при определении превышений методом тригонометрического нивелирования.

Ответ 9.9.4. Как можно приравнять iиl? Практически на рейке нужно отложить величину, равную высоте прибора и при измерений вертикального угла навести горизонтальную нить на эту точку. Можно это сделать при тригонометрическом нивелировании? Конечно. Тогда какой вид примет формула?

9.9.5. Если расстояние между точками измеряют дальномером с вертикальной рейкой, то подставив в формулу вместо d его значение d=К lcos²υ после несложных преобразований получим:

h = 1|2 К lsin²υ или h = 1|2 D lsin2υ ,

где D - расстояние, измеренное дальномером.

При определении превышений по этим тахеометрическим форму­лам, пользуются тахеометрическими таблицами.

9.9.6. По общим правилам теории погрешностей можно определить среднеквадратическую ошибку m_h превышения, определяемого мето­дом тригонометрического нивелирования.

Действующие инструкции допускают расхождения в превышениях двух соседних точек 4 см на каждые 100 м расстояния между точками.

Раздел 4. ПЛАНОВЫЕ ТОПОГРАФИЧЕСКИЕ СЪЕМКИ

Глава 10. Съемка местности и ее виды.

10.1. Съемка местности

10.1.1. Съемкой называется совокупность угловых и линейных изме­рений, производимых на земной поверхности для создания планов, карт, профилей.

Съемки подразделяются на два основных вида: наземные и воз­душные или аэрофотосъемка.

В зависимости от целевого назначения наземные съемки подраз­деляются на горизонтальную или контурную в результате, которой получают план с изображением только ситуации без отображения рельефа и горизонтально-вертикальную или топографическую для получения плана с изображением как ситуации, так и рельефа.

Для получения только рельефа или его высотных характеристик применяют высотную или вертикальную съемку.

В зависимости от применяемых инструментов по наименованию их, съемки классифицируются на:

- теодолитную, выполняемую теодолитом и мерной лентой, по ре­зультатам которой получают ситуационный или контурный план;

- тахеометрическую, производимую теодолитом-тахеометром с изображением на плане ситуации и рельефа местности;

- мензульную, выполняемую при помощи мензулы и кипрегеля. План вычерчивается непосредственно во время съемки с изображением рельефа и ситуации;

- фототеодолитную, которая производится фототеодолитом. План может быть, как контурный так и топографический;

- аэрофотосъемку, выполняемую специальными фотокамерами с самолета. Производится в сочетании с геодезическими работами, необ­ходимыми для привязки снимков к местности в плановом и высотном отношениях;

- буссольную, выполняемую с помощью буссоли. Применяется в основном, как дополнительная при других видах съемок;

- глазомерную, производимую на папке-планшете с помощью компаса и визирной линейки. Имеет место для получения ориентировоч­ного плана местности.

10.2. Способы съемки подробностей

(ситуации и рельефа) местности

10.2.1. Съемку ситуации и рельефа на местности выполняют сле­дующими способами: перпендикуляров или прямоугольных координат, полярных координат, угловых и линейных засечек, обхода и створов.

Выбор способа зависит от вида съемки, условий местности, т.е. от снимаемых объектов и рельефа, а также от масштаба, в котором строится план.

Съемка подробностей производится по характерным точкам /пи­кетам/.

Пикеты могут быть контурные, которые выбираются на изломах контуров, высотные - выбираемые в характерных точках рельефа и контурно-высотные.

Успех съемки во многом зависит от правильного выбора пикетов. На местности они не закрепляются.

Способ перпендикуляров или прямоугольных ординат применяется при горизонтальной съемке контуров, расположенных вблизи тео­долитного хода. Съемка производителя относительно сторон теодолитного хода (рис.4.1а).

Из характерной точки «а» на сторону 2-3 опускают перпен­дикуляр и рулеткой замеряют его длину (15,8 м), затем по стороне хода от начальной точки 2 до перпендикуляра берут второй замер лентой (11,5м). Таким образом, на каждую характерную точку берут два замера перпендикулярно друг другу.

Перпендикуляры на местности строят с помощью эккера (устрой­ство и работа с ним даны в п.5.7).

Длины перпендикуляров не должны превышать 40 м для съемки 1:2000, 20м для 1:500 (при работе с эккером) и 5, 10 м (без экке­ра), т.к. с увеличением длины перпендикуляров возрастает погрешность определения положения снимаемых точек.

Способ полярных координат - применяют при съемке ситуации и рельефа местности. Съемка производится с точки теодолитного хода 2, являющейся полюсом, относительно сто­роны 2-3, принимаемой за полярную ось (рис.4.1б).

В точке 2 устанавливают теодолит и нулевым отсчетом на лимбе горизонтального круга направляют по стороне 2-3. Положение снимаемой точки В определится горизонтальным углом b=59°45 и расстоянием Д = 28,5м, измеренных по дальномеру (две полярные ко­ординаты). Высотные положения этой точки получают по углу наклона n являющейся третьей полярной координатой.

По углу наклона и расстоянию по формуле тригонометрии вычис­ляют превышения h.

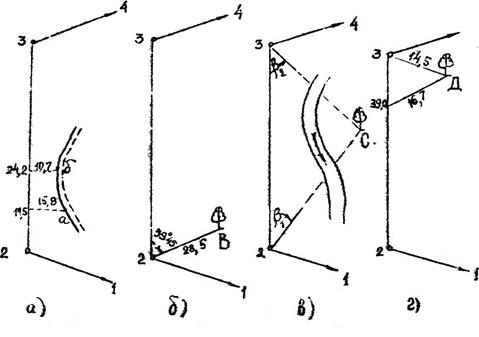
Рис.4.1 Способы съемки подробностей при теодолитной съемке

Способ угловых засечек - применяют при съемке труднодоступ­ных точек (рис.4.1в). Сторону 2-3 теодолитного хода принимают за базис. С точки 2 между базисом и направлением на снимаемую труднодоступную точку С замеряют горизонтальный угол b₁. Затем замеряют горизонтальный угол b₂ с точки 3. Положение точки С на плане определится засечкой двух нап­равлений по углам b₁ и b₂.

Способ линейных засечек - применяют, когда снимаемые объек­ты расположены вблизи планового обоснования. Положение точки Д (рис.4.1г) определяют двумя замерами 16,7 и 14,5 м относительно стороны рабочего обоснования.

Способ створов применим тогда, когда снимаемый объект рас­положен по створу стороны теодолитного хода, в данном способе определяют расстояние лентой или рулеткой по створу от точки 3 до точки Е (рис.4.1д).

Способ обхода - применяется на застроенных участках при съем­ке контуров леса и других объектов и заключается в том, что по грани­цам данного контура прокладывают теодолитный ход, который опреде­ляет контур объекта.

ВОПРОС. В какой съемке применяют способ перпендикуляров?

1. В тахеометрической (п. 10.2.2)

2. В теодолитной (п. 10.2.3).

Ответ 10.2.2. Неправильно. Тахеометрическая съемка - горизонтально-вер­тикальная. Для определения положения точки по высоте способ перпендикуляров не имеет применения. В этой съемке применяют полярный способ

Ответ 10.2.3. Правильно. Способ перпендикуляров применим при теодолитной съемке.

ВОПРОС. В каких съемках применяют способ угловых засечек?

1. В любых съемках (п. 10.2.4).

2. В теодолитной (п. 10.2.5).

Ответ 10.2.4. Действительно, этот способ применяют при любой съемке, но этот способ дает только плановое положение точки.

Ответ 10.2.5. Правильно, применим.

Глава 11. Теодолитная съемка.

11.1. Общие сведения..

11.1. Теодолитная съемка производится на относительно неболь­ших участках земной поверхности с целью получения плана данной местности с изображением на нем местных предметов (ситуации).

Съемка производится следующими инструментами и приборами: теодолитом, 20 или 30 м стальной лентой с комплектом шпилек, эк­лиметром, рулеткой, эккером с применением вешек.

Она делится на два основных этапа:

1. Полевые работы - выполняются в поле, где производится измерение горизонтальных углов, длин сторон теодолитного хода и съемка подробностей.

2. Камеральные работы - выполняются после полевых измерений и они сводятся к обработке материала, полученного в результате съемки в поле и построению плана.

ВОПРОС. Что следует понимать под теодолитной съемкой?

1. Съемка местности, снимаемая теодолитом (11.1.2).

2. Горизонтальная съемка контуров местности и местных пред­метов, выполняемая теодолитом и стальной мерной лентой (п. 11.1.3).

Ответ 11.1.2. Ваш ответ будет неполным, так как теодолитом производят и другие съемки, в частности, тахеометрическую.

Ответ 11.1.3. Ответ верный. Кратко и конкретно отвечает, что съемка горизонтальная характеризуется съемкой ситуации без отображения рельефа местности.

11.2. Полевые работы.

11.2.1. В полевые работы входит проложение теодолитного хода, который является съемочным обоснованием, и съемка подробностей. Подробно о полевых работах в теодолитных ходах рассмотрено в п.8.2

После проложения теодолитного хода приступают к съемке под­робностей, которая опирается на этот теодолитный ход. Известно несколько способов съемки подробностей, но применяют как правило способ перпендикуляров или ординат, а также ли­нейных засечек.

Объектами съемки являются местные недвижимые предметы, как например: леса, огороды, пашни, водоемы, дороги, строения и другие естественные и искусственные сооружения, относящиеся к ситуации. Съемка подробностей заключается в определении на местности харак­терных точек контуров местных предметов: повороты, изгибы и т.д.

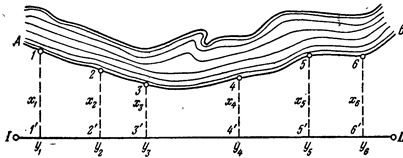
Рис. 4.2. Принцип съемки ситуации

Пример: Из характерной точки 1,2,…п (рис. 4.2) на сторону теодолитного хода 1-2 промеряется по перпендикуляру расстояние.. Второй замер делают по стороне 1-2 от начальной точки хода до основания перпендикуляра. Таким образом, определи­лось положение любой характерной точки. И так ведут съемку каждой характерной точки ситуации. Замеры делают до десятых долей метра. Прямые углы на местности строят с помощью эккера ( п. 5.7).

ВОПРОС. Какова роль характерных точек?

1. От характерных точек зависит степень передачи подобия снимаемых объектов на плане (п. 11.2.2)

2. Роль их незначительна, так как снимают их с меньшей точностью, чем точки теодолитного хода (п. 11.2.3).

Ответ 11.2.2. Совершенно правильно. Именно от правильного выбора характерных точек зависит подобие передачи снимаемых местных предметов на план. Поэтому точки, по которым снимаются подробности, должны быть характерными.

Ответ 11.2.3. Неверно. Роль их значительная при передаче подобия. Снимают их с меньшей точностью потому, что при неправильном измерении положения точки, ошибка будет только в данной точке и не повлечет за собой ошибку в определении положения других точек, как это име­ет место в теодолитном ходе.

Результаты съемки подробностей заносят в абрис.

Абрис составляют для каждой стороны хода отдельно. На обыч­ной бумаге в схематичной форме изображают заснятые контуры по характерным точкам с обозначением местных предметов в условных зна­ках. Абрис составляется в карандаше.

Для каждой характерной точки выписываются значения двух проме­ров (рис.4.3).

ВОПРОС. Что такое абрис и его назначение?

1. Схематичный чертеж, составленный в полевых условиях по дан­ным измерений (п. 11.2.5).

2. Зарисовка местности (п. II.2.6).

Ответ 11.2.5. Действительно, это схематичный чертеж, на котором предс­тавлены снимаемые объекты по характерным точкам относительно ли­ний теодолитного хода. Он служит исходным материалом при составлении плана.

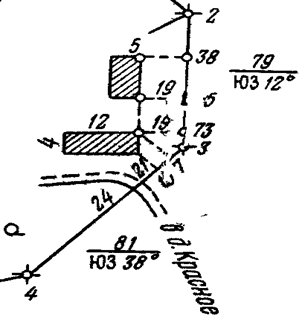
Рис.4.3.Способ перпендикуляров

Ответ 11.2.6. Такое определение будет не точным. Абрис является исходным материалом для изображения подробностей на плане. Поэтому аб­рис должен составляться исключительно по тем характерным точкам, которые были взяты на местности при съемке подробностей.

11.3. Камеральные работы (построение план)

11.3.1. План строят на листе ватмана и начинают с построения координатной сетки. Размер стороны квадрата сетки в зависимости от масштаба, в котором строят план, может быть 4, 5 и 10 см. Чаще принимают 10 см.

Координатную сетку строят с помощью линейки Дробышева или циркуля, поперечного масштаба и линейки.

Рассмотрим построение с помощью циркуля, поперечного масшта­ба и линейки. Нa листе бумаги с угла на угол по диагоналям проводят прямые линии. Из точки пересечения циркулем-измерителем откладывают по к ним отрезки произвольной, но равной длины так, чтобы оставались по ля сверху и снизу примерно по 10 см., а с боков около 5 см.

Концы отрезков соединяют прямыми линиями и получают прямоугольник. Стороны прямоугольника делят пополам и через середины противоположных сторон проводят прямые, которые должны пройти че­рез точку пересечения диагоналей, из середины каждой стороны в обе стороны откладывают отрезки, равные стороне координатной сетки (в нашем случае 10 см) и точки деления противоположных сторон сое­диняют прямыми линиями. Все остальные лишние линии стирают.

Правильность построения сетки проверяют по диагоналям квад­ратов координатной сетки. Вертикальные линии сетки принимаются параллельными осевому меридиану или оси Х, а горизонтальные - оси У.

ВОПРОС. С какой целью вычерчивается координатная сетка?

1. Чтобы привязать теодолитный ход (п. 11.3.2).

2. Для точности нанесения точек теодолитного хода по их коор­динатам (п. 11.3.3).

Ответ 11.3.2. Ответ неверный. Теодолитные хода привязыва-ют к геодезическим пунктам государственной сети посредством измерений на мест­ности для передачи координат с геодезического пункта на первую точку теодолитного хода, но не к координатной сетке.

Ответ 11.3.8. Правильно. При нанесении на план точек по их координа­там часто приходится откладывать отрезки, превышающие нормальный раствор циркуля-измерителя, поэтому для более точной накладки пред­варительно строят сетку квадратов.

ВОПРОС. Почему необходимо проверять построение координатной сет­ки?

1. Потому, что от нее зависит точность построения плана (п.11.З.4).

2. Координатная сетка является основой при построении плана, на которую наносят вершины теодолитного хода, поэтому она должна быть построена без ошибок (п. 11.3.5).

Ответ 11.3.4. Не совсем так. Точность построения плана, зависит не только от точности построения координатной сетки, а также от масштаба, точности съемки и т.д.

Ответ 11.3.5. Ответ правильный и полный.

11.3.6. Координаты координатной сетки определяют таким образом, чтобы теодолитный ход разместился в середине плана. Для этого из ведомости координат берут min и max значения координат Х и У. Округляют их по max значению, в большую сторону до ближай­шего числа, кратного стороне координатной сетки.

Для нашего примера со стороной 10 см при масштабе плана 1:1000, сторона координатной сетки равна 100 м.

Max значения X = 126,04 , У= 103,59, следовательно, округляют до 200 м.

Аналогично делают по min значениям.

В нашем примере min значения X и У равны 0 (точка № 1).

Имея в виду, что на план будет нанесена ситуация не только внутри теодолитного хода, но и за его пределами, необходимо добавить квадраты координатной сетки со следующим min значением ко­ординатной сетки - 100 по осям координат Х и У.

Таким образом, определились крайние значения координат сетки от -100 до +200. Подписывают координаты около координатной сет­ки, затем наносят точки на план (рис.4.4).

Рис. 4.4. Построение координатной сетки

ВОПРОС. Определите необходимое число квадратов координатной сетки размером стороны 10 см для построения плана масштаба 1:500, последующим значениям координат теодолитного хода:

Хmax = 123,8 Уmax = 67,18

Хmin = -56,05 Уmin = - 109,85

1. 4x4 квадрата (п. 11.3.7).

2. 5 х 5 квадрата (п. 11.3.8).

Решение вопроса начинают с определения размера стороны квадрата координатной сетки с учетом масштаба. Масштаб дан 1:500, следовательно, в I см - 5 м, а в 10 см - 50 м.

Ответ 11.3.7. Ответ неправильный. В данном решении исходили из варьирования координат от max до min. значений по осям X и У, а именно по Х координаты меняются от 123,39 до -56,05, т.е. в сумме на 179,94 м, аналогично по У - на 177,03 и

После деления этих сумм на 50 м получают по 4 квадрата по X и У.

Ответ 11.3.8. Ответ верный, max и min значения координат по X и У округляют до ближайших к ним значениям координатной сетки в сторону увеличения по max и в сторону уменьшения по min. По Х эти значения будут 150 и –100, по У - 100 и -150 м.

Таким образом, потребуется по 5 квадратов.

11.3.9. Для накладки точек теодолитного хода сетку подписы-вают так, чтобы весь ход разместился в средней части листа.

В начале по вычисленным координатам определяют квадрат, где должна находятся вершина теодолитного хода (рис.4.5).

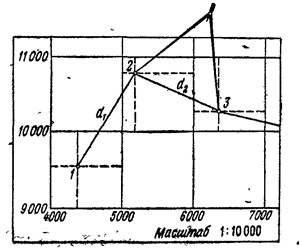
Рис. 4.5. Нанесение на план точек теодолитной съемки

Непосредственно накладку каждой точки хода производят с помощью циркуля-измерителя и поперечного масштаба. Вначале по координатам точки устанавливают, в каком квадрате она находится. Затем циркулем-измерителем откладывают соответст-вующие отрезки в масштабе по сторонам квадрата, применяя поперечный масштаб (см. п.3.2.I.). Соединяют подученные отрезки прямой линией. Аналогично накладывают остальные точки.

Правильность накладки теодолитного хода на план проверяют сравнением дирекционных углов по каждой стороне, измеренных транс­портиром непосредственно с плана с вычислениями, а также длины сторон измеренных по плану с помощью поперечного масштаба с ее горизонтальными проекциями,

ВОПРОС. С какой целью проверяют накладку теодолитного хода на план?

1.Чтобы вскрыть ошибки в теодолитном ходе:

а) при его проложении (п. 11.3.9).

б) при его вычислении (п. 11.3.10).

2. Теодолитный ход является рабочим обоснованием, на базе которого строится план, поэтому он должен быть нанесен 6eзошибочно (п.11.3.11).

Ответ 11.3.10. Неправильно. Так как ошибки, допущенные теодолитном ходе в процессе полевых измерений или при вычислении координат, вскрывают ранее с помощью проме-жуточных контролей и невязок (см. п.8.3.21).

Ответ 11.3.11. Правильно. Теодолитный ход является основой, по которой строится план местности.

11.4. Построение ситуации на плане.

11.4.1.. После проверки правильности нанесения теодолитного хода приступают к накладке на план ситуации, т.е. контуров и предметов местности, используя при этом абрис съемки подробностей.

Каждую характерную точку наносят по двум замерам. Один за­мер с абриса берут по стороне хода и с помощью измерителя и попе­речного масштаба в масштабе плана откладывают на соответствующей стороне плана от начальной точки стороны. Второй замер от конца этого отрезка по перпендикуляру.

Таким образом, получают положение характерной точки местнос­ти на плане. Соединяя характерные точки, взятые на одном предмете местности или контуре, получают на плане их изображение.

ВОПРОС. Можно ли использовать простую линейку при накладке ситуации на план?

1. Можно (п. 11.4.2).

2. Это зависит от масштаба, в котором строится план (п. 11.4.3).

Ответ 11.4.2. Ответ не совсем правильный. В одних случаях можно, в других нельзя. Это зависит от масштаба плана.

Ответ 11.4.3. Ответ правильный. Как известно на линейке наименьшее де­ление равно I ми. В зависимости от численного масштаба, в котором строят планы, наименьшее деление на линейке может соответствовать 0,5 м (при М 1:500) или 5 м (при М 1:5000). Отсюда следует исходить. При крупном масштабе можно, при мелком - нет.