РАЗМЕЩЕНИЕ РЕБЕР ЖЕСТКОСТИ

Гибкость стенки пролетной балки в ее средней части

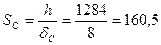
Здесь h и δ_C — высота и толщина стенки соответственно.

Обычно при 160<S_С<265 для малоуглеродистой стали ус­танавливают поперечные и одно продольное ребро жесткости. Поперечные ребра (диафрагмы) выполняются из листового проката. Ширину выступающей части ребра (рис. 10.9) опре­деляют по условию: 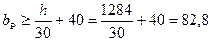мм.

Принимается ширина b_Р=90мм. Толщина ребра из усло­вия обеспечения его устойчивости: 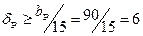мм.

Момент инерции ребра относительно плоскости стенки должен быть 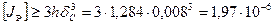м⁴, фактический же с учетом двух частей стенки шириной 20δ_С по обе стороны от ребра

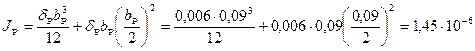м⁴.

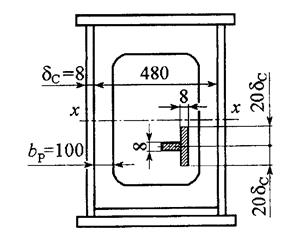
Рис. 10.9. Установка большой диафрагмы

Поскольку 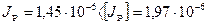м⁴, увеличим толщину ребра до δ_Р=8 мм, а ширину b_Pдо 100 мм. Тогда 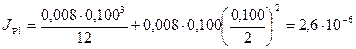м⁴, что больше требуемого значения.

Шаг поперечных ребер для обеспечения прочности рельса должен быть

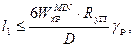
где 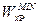— минимальный момент сопротивления рельса; R_уп=350 МПа — нормативное сопротивление материала рельса; D=128 кН — давление колеса тележки (см. рис. 4.3); γ_р=0,5 — коэффициент условий работы рельса.

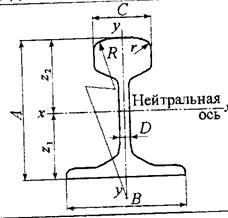
В соответствии с этими условиями при ширине поверхности катания колеса (диаметром D_K=400 мм) В₁ =80 мм(табл.7.1) устанавливается рельс с шириной головки 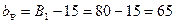мм. Этому размеру соответствует рельс Р43, минимальный момент сопротивления которого 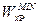= 208 см³ (табл. 10.2).

Таблица 10.2

Основные данные железнодорожных рельсов

Тип рельсов	Основные размеры, мм	ГОСТ на конструкцию и размеры
A	B	C	D	R	r
Р8 Р11 Р18	80,5				-		ГОСТ 6368-82
Р24 Р43 Р50				10,5 14,5			ГОСТ 7173-54 ГОСТ 7174-75
1Р65 2Р65							ГОСТ 8161-75
Тип рельсов	Расчетные данные	Масса 1 м рельса, кг
Площадь поперечного сечения, см2	z1, см	z2, см	Моменты инерции, см4	Моменты сопротивления, см3
Jx	Jy	W1	W2	W3
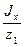
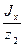
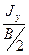
Р8 Р11 Р18 Р24 Р43 Р50 1Р65 2Р65	10,76 14,28 22,88 31,79 65,99 82,65 82,79	2,89 3,96 4,31 5,33 6,85 7,05 8,13 8,17	3,61 4,09 4,69 5,47 7,15 8,15 9,87 9,87	60,21 126,6 238,4 497,8	9,88 17,06 40,68 86,1	20,86 31,99 55,36 93,39 217,3 -	16,66 30,93 50,81 91,02 208,3 -	3,66 5,17 10,17 18,72	8,42 11,18 17,91 24,90 44,65 51,67 64,72 64,98

При этих параметрах шаг поперечных ребер

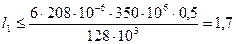м.

Учитывая, что верхний пояс пролетной балки достаточно тонок, для обеспечения его прочности при действии местных напряжений от давления колес тележки принимаем конструк­тивно шаг малых диафрагм 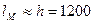мм, шаг больших диа­фрагм l_Б=3l_М=3·1200=3600 мм.

Проверка прочности поперечного ребра по условию ра­боты его верхней кромки на сжатие делается по формуле

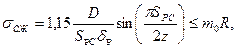
где 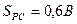- длина линии контакта рельса и пояса над ребром; B=0,114м - ширина подошвы рельса Р43 (см. табл. 10.2). Тогда 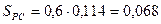м, D=128 кН; R=243МПа - расчетное сопротивление материала при сжатии; 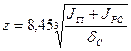- расчетная зона распределения давления колеса по ребру; 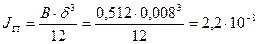м⁴- момент инерции пояса; 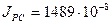м⁴ - момент инерции рельса (см. табл. 10.2); 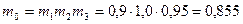- коэффициент условий работы.

Тогда 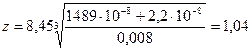м.

Таким образом, напряжение сжатия 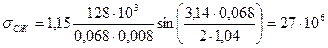Па, что намного меньше допустимого напряжения т₀R = 0,855 • 243 = 208 МПа.

Проверку прочности верхнего пояса между диафрагмами необходимо проводить в силу того, что он испытывает напряжения от местного изгиба, деформируясь совместно с рельсом.

Величины местных напряжений:

вдоль оси балки

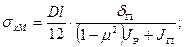(10.1)

поперек оси балки

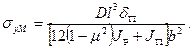(10.2)

В этих выражениях l=1,2 м — расстояние между диафраг­мами; δ_П=0,008 м — толщина пояса; μ— коэффициент Пуассона; J_P=14,89·10^-6 м⁴ — момент инерции рельса; b=0,48м — размер «в свету» между стенками балки.

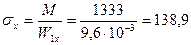МПа.

Подставив числовые значения параметров в формулы (10.1) и (10.2), имеем:

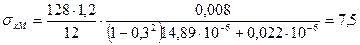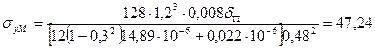МПа,

МПа.

Прочность пояса с учетом напряжений σ_x общего изгиба балки проверяется по приведенным напряжениям для плоского напряженного состояния:

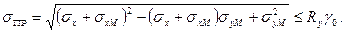(10.3)

Подставим в это уравнение параметры, полученные выше:

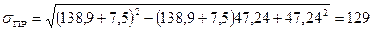МПа.

Расчетное сопротивление материала:

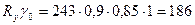МПа>129 МПа,

и следовательно, прочность верхнего пояса обеспечена.

Местная устойчивость стенок при действии нормальных напряжений обеспечивается установкой диафрагм. Проверка производится по условию (8.11):

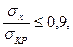
где 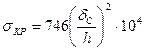- критическое напряжение, при котором происходит потеря устойчивости.

Подставив значения толщины δ_С и высоты стенки h в середине пролета, имеем

МПа.

Отношение нормальных напряжений (σ_x =138,9 МПа) к критическим 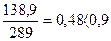, что говорит о достаточно высокой устойчивости стенок.

Продольное ребро жесткости.

При жесткости 160≤S≤265, как указывалось в начале раздела, рекомендуется ставить одно продольное ребро. В нашем примере 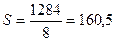, и в силу незначительного превышения границы необходимость установки продольного ребра жесткости отпадает.