ПРОЧНОСТЬ ПРОЛЕТНОЙ БАЛКИ ПРИ ЕЕ ОБЩЕМ ИЗГИБЕ В ДВУХ ПЛОСКОСТЯХ

Проверку прочности балки в средней части пролета про­изводим при действии нагрузок комбинации 1.1. Б.

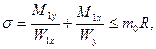(10.5)

где 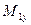и — и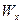згибающий момент и момент сопротив­ления в вертикальной плоскости. Значения 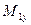=1333 кН·м и 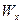=9,6·10^{-3 м3} берем из выше произведенных расчетов; 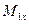и 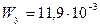м³ - изгибающий момент и момент со­противления в горизонтальной плоскости; R=243 МПа — расчетное сопротивление материала; т₀=0,855 — коэффициент условий работы (см. выше).

Схема приложения горизонтальных нагрузок приведена на рис. 10.10. |

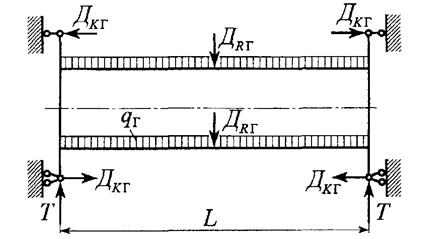
Рис. 10.10. Схема приложения горизонтальных нагрузок

Горизонтальные инерционные нагрузки рассчитываются по формуле

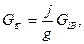
где 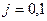м/с² — ускорение крана при пуске механизма; g=9,81 м/с² — ускорение силы земного притяжения; 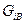- расчетные силы веса изделий, создающих инер­ционные нагрузки.

При 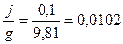горизонтальные инерционные нагрузки будут равны:

от распределенной нагрузки 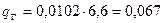кН/м;

от веса кабины 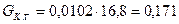кН;

от привода передвижения 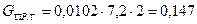кН;

от веса груза и тележки 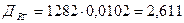кН.

Суммарный горизонтальный момент в среднем сечении пролета определим по выражениям

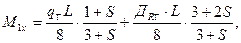(10.6)

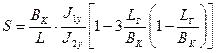, (10.7)

где В_K=5,6 м — база крана; 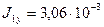м⁴ — момент инер­ции пролетной балки в горизонтальной плоскости (см. выше); 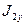— момент инерции концевой балки в горизон­тальной плоскости,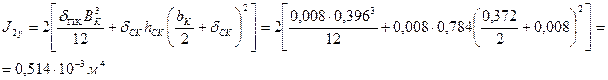

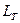- база тележки.

Подставляя численные значения параметров в формулы (10.6), (10.7), получим:

,

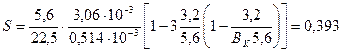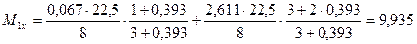кН·м.

Напряжения в балке определяем по формуле (10.5):

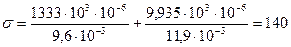МПа, что не превышает сопротивления материала 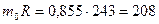МПа.