ПРОЧНОСТЬ И УСТОЙЧИВОСТЬ СТЕНОК

Стенка под рельсом

Стенка под рельсом нагружена нормальными напряжениями от общего изгиба, местными нормальными напряжениями от давления колес тележки и касательными напряжениями среза от поперечной силы при общем нагружении балки и дополнительными касательными напряжениями от эксцентриситета нагрузки.

Нормальные напряжения в стенке от общего изгиба на уровне верхнего пояса

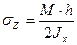(6.10)

где М.- общий изгибающий момент для балки по формуле (4.2); h - высота стенки; J_х — общий момент инерции балки.

Местные напряжения сжатия на кромке стенки от давления колеса, передающегося на стенку через рельс и пояс,

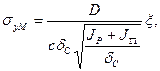(6.11)

где σ_уМ — местные напряжения сжатия кромки стенки в вертикальной плоскости; D — давление колеса; с — ко­эффициент, учитывающий способ соединения пояса и стенки: для сварных и прокатных балок с=3,25, для клепа­ных с=3,75; δ_C — толщина стенки; J_P и J_П — моменты инерции рельса и пояса относительно собственных ней­тральных осей; ξ— коэффициент, учитывающий разгру­жающее влияние поперечных ребер жесткости.

При определении J_П в расчет вводится часть пояса шириной от его наружного края до расстояния 10... 12 значений толщины пояса от оси стенки внутрь балки, но не менее ширины подошвы рельса.

График коэффициента ξ для сварных балок приведен на рис.6.4. На графике 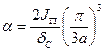, (6.12)

где а - расстояние между ребрами жесткости.

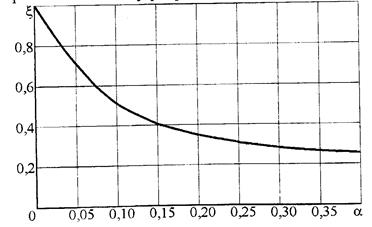
Рис. 6.4. График коэффициента влияния ребер ξ

Влияние ребер практически не сказывается (ξ=1) при а=70δ_С, а заметное уменьшение местных напряжений на кромке стенки получается лишь при а=(40...50)δ_С. Так часто целесообразно располагать лишь короткие ребра, длина кото­рых должна быть не менее 0,3h, где h — высота стенки.

Касательные напряжения среза от суммарной поперечной силы (см. формулу 6.8)

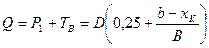(6.13)

в предположении, что её воспринимает только стенка,

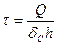. (6-14)

Прочность стенки при плоском напряженном состоянии проверяется по условию:

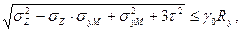(6.15)

где 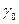— коэффициент неполноты расчета (по формуле 5.2) и табл. 5.1 ...5.5); R_у - расчетное сопротивление материала(табл. 1.2, 1.3).

Устойчивость стенки при действии только касательных напряжений проверяется по указаниям раздела 8.3.4.

При совместном действии нормальных напряжений от общего изгиба балки 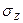, и местных нормальных напряжений, а также касательных напряжений τ местная устойчивость проверяется по условию:

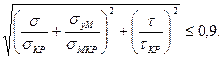(6.16)

Величина критических напряжений среза τ_кр определяется по формуле (8.9). Критические нормальные напряжения существенно зависят от соотношения размеров отсека пластинки 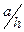, где а — шаг диафрагм, и от соотношения местных и общих нормальных напряжений в соответствии с данными табл. 6.1.

Таблица 6.1

Коэффициенты для проверки устойчивости стенок сварных коробчатых балок [ 1 ]

Коэффи­циенты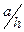
0,5	0,8	1,0	1,2	1,4	1,6	1,8	2,0
К1
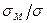
			0,112	0,300	0,633	1,283	2,249	3,939
К2

Примечание. При 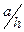>2 значения коэффициентов равны их г величинам при 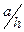=2,0.

При 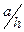≤0,8 критические напряжения от общего прогиба

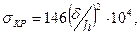МПа, (6.17)

а от местного напряжения

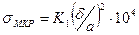,МПа. (6.18)

При 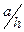=0,8, если 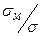больше значений, указанных в табл.6.1, то местные критические напряжения

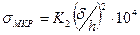,МПа; (6.19)

если 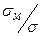не больше значений, указанных в табл.6.1, то местные напряжения определяются по формуле (6.18), но с подстановкой а/2 вместо а как в формулу (6.18), так и в табл. 6.1.

В обоих случаях 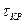вычисляется по действительным размерам отсека.

При высоких значениях сжимающих напряжений для устойчивости стенки применяют кроме основных поперечных ребер жесткости продольные ребра на расстоянии (0,25...0,3)h от сжатого пояса и доходящие до продольного ребра короткие поперечные ребра. В этом случае каждый отсек проверяется отдельно (см. 8.3.5) с учетом приведенных выше формул для определения критических напряжений. 1

Свободная стенка

Прочность и устойчивость свободной стенки проверяется по методике, приведенной в 8.3.4и 8.3.5.