Информация в непрерывных сообщениях.

Цель работы. Изучение методов определения количества информации в непрерывных сообщениях.

Теоретическое обоснование. Непрерывные сообщения - это сообщения, построенные на основе бесконечного алфавита, поэтому соотношения, используемые для определения количества информации в дискретных сообщениях для них в общем случае не применимы. Исключение составляют лишь непрерывные сообщения, у которых символы появляются равновероятно, спектр ограничен, а сами они проявляются на некотором уровне шумов.

Действительно, такие сообщения могут быть представлены дискретными сообщениями с объемом алфавита, равным числу различимых уровней, и числом символов в сообщении, определяемым теоремой Котельникова. Количество информации содержащейся в них может быть посчитано с помощью формулы Хартли.

Число различимых уровней (L) определяют на основе соотношения:

,

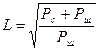где Р_с ― мощность сообщения (сигнала);

Р_ш ―мощность шума.

В соответствии с теоремой Котельникова, для передачи непрерывного сообщения длительностью Т(сек) и граничной частотой в спектре F_m(сек^-1)достаточно передать его равноотстоящие мгновенные значения с интервалом ∆t (сек)и общим числом N , причем ∆t≤1/2F_m. и N≥2TF_m+1.

Используя формулу Хартли, количество информации, содержащееся в таком непрерывном сообщении, (I) и его энтропия (H) могут быть найдены по формулам:

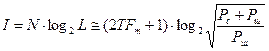(бит);

.

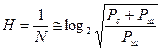
В общем случае, когда символы непрерывного сообщения появляются неравновероятно и их закон распределения описывается некоторой функцией плотности распределения вероятности p(x), (p(x) характеризует вероятность попадания символа непрерывного сообщения x в некий интервал ∆x), для подсчета информационных характеристик пользуются формулой для подсчета энтропии непрерывных сообщений.

Общая энтропия непрерывных сообщений, как показано в §1.8, равна бесконечности, однако выражение, ее описывающее, представляет собой сумму двух слагаемых, одно из которых стремится к бесконечности одинаковым образом для любых непрерывных сообщений, а второе является конечным и зависит от закона распределения символов непрерывного сообщения. Это слагаемое и называется дифференциальной или относительной энтропией.

Дифференциальная энтропия (H_x) определяется выражением:

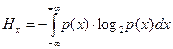
Практическое использование дифференциальной энтропии основано на предположении, что непрерывные сообщения проявляются на некотором уровне аддитивных шумов (что всегда справедливо для реальных сообщений). В этом случае энтропия реального непрерывного сообщения Н равна разности энтропий принятого (зашумленного) сообщения (Н_с) и шума (Н_ш), то есть

Н = Н_с + Н_ш.

Содержание работы.

1.Подсчитать количество информации в реальном непрерывном сообщении при наличии аддитивного шума при условии, что символы сообщения появляются равновероятно.

В качестве такого непрерывного сообщения использовать сигнал U(t) вида:

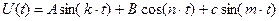
где k— Ваш номер по списку;

n=k+2;

m=k+4;

A, B, C берется из таблицы и определяется Вашим номером по списку.

Длительность сигнала U(t) равна 2 сек. (Т = 2сек.). В качестве аддитивного шума использовать случайный сигнал X(t), получаемый с помощью генератора случайных чисел. Значения шума лежат в интервале от –D/2 до D/2 (D=1,2).

2.Подсчитать дифференциальную энтропию зашумленного аддитивным шумом сигнала Q(t)=U(t) + X(t) и дифференциальную энтропию шума X(t) и определить среднее количество информации, приходящееся на один символ, которое может быть извлечено из зашумленного сигнала Q(t),считая, что все сигналы принимают свои значения с равной вероятностью.

Выполнение работы Работа выполняется на персональном компьютере в среде программного продукта «Mathcad»:

П.1.а). Построить графики сигналов U(t), X(t) и Q(t) = U(t) + X(t).

б). Представить непрерывный сигнал Q(t) в виде последовательности отсчетов, в соответствии с теоремой Котельникова. Следует учесть, что максимальная частота в спектре сигнала U(t) определяется круговой частотой m (размерность: рад/сек), а максимальная частота спектра, входящая в выражение теоремы Котельникова, является циклической частотой (размерность сек^-1=гц), поэтому справедливо соотношение

.

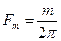в). Построить на одном экране графики Q(t) и Q_k(t), где Q_k(t)- график взятия выборок сигнала Q(t).

г). Вычислить мощность полезного сигнала Р_с и мощность шума Р_ш по формулам

.

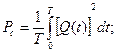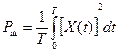
д). Найти количество информации (I), содержащееся в непрерывном сообщении при наличии аддитивного шума, и его энтропию (Н).

П.2.а). Выразить аналитически функцию плотности распределения вероятности значений сигнала Q(t) и построить ее график.

Так как сигнал U(t) и шум X(t), по условию, принимают свои значения с одинаковой вероятностью, то и сигнал Q(t)=U(t)+ X(t) будет принимать все свои значения равновероятно во всем диапазоне значений от -(A+B+C+D/2) до (A+B+C+D/2).

Поэтому его функция плотности распределения вероятности p(Q) (с учетом того, что ) имеет следующий вид:

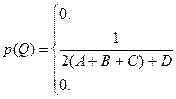
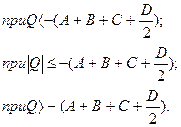
Программа вычисления этой функции может быть реализована на основе оператора условного перехода if следующим образом:

Q := -10, –9,9….10

.

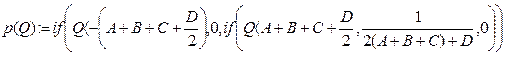б). Выразить аналитически функцию плотности распределения вероятности шума p(x) и построить её график аналогично тому, как это сделано для функции плотности распределения вероятности сигнала Q(t):

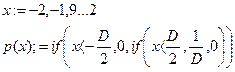
в). Определить дифференциальную энтропию сигнала Q(t) и дифференциальную энтропию шума X(t) в соответствии с определением дифференциальной энтропии:

.

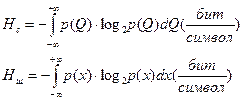г). Найти среднее количество информации, приходящееся на один символ зашумленного сигнала, как разность между Н_с и Н_ш и сравнить ее с энтропией зашумленного сигнала Н, вычисленного в п.1 этой лабораторной работы.

Контрольные вопросы

1. Какие источники сообщений называют непрерывными?

2. Сформулируйте теорему Котельникова.

3. Какое соотношение определяет число различимых уровней непрерывного сообщения при наличии аддитивного шума?

4. Дайте определение дифференциальной энтропии.

5. Чему равна полная энтропия непрерывного сообщения и из чего она слагается?