Методические указания к выполнению курсового проекта
Система управления состоит из набора различных компонентов, выполняющих определенные функции по отношению к внешнему окружению системы. Чтобы иметь возможность воспринимать информацию извне и передавать ее для управления, система должна иметь входы и выходы. Так, например, ввод информации в станок осуществляется с помощью штурвалов или рычагов, приводимых в действие оператором. Выходом системы является движение режущего инструмента. Функция станка заключается в изменении размеров и формы сырьевой заготовки при помощи режущего инструмента, движение которого задается входной информацией, введенной оператором. Более сложные электронные системы используются в задачах комплексных измерений. Эти системы конструируются из стандартных электронных элементов и мотивируются с жесткой конфигурацией.
Микрокомпьютер в отличие от других электронных компонентов не обладает фиксированным набором функциональных характеристик. Его характеристики определяются во время проектирования системы, используя процесс, который называется программированием. Неограниченный диапазон программируемых функциональных возможностей микрокомпьютера и придает ему особое значение. Электронные компоненты системы (в том числе и микрокомпьютер), которые называются аппаратными средствами (nardware) или техническими, являются сравнительно жесткими и трудно поддающимися изменениям после того, как параметры этих компонентов выбраны и система построена. В противоположность выше сказанному программные компоненты, создаваемые во время проектирования и называемые программным обеспечением (software), относительно легко могут быть изменены даже после того, как проектирование завершено и система управления сконструирована.
Формализация и преобразование связей между логическими
Переменными
Устройства ЭВМ состоят из элементарных логических схем. Работа этих схем основана на законах и правилах алгебры логики, которая оперирует двумя понятиями: истинности и ложности высказывания. Высказывания называются логическими двоичными переменными и обозначаются 1 и 0 соответственно. Высказывания могут быть простые, если содержат одно законченное утверждение, и сложные, содержащие два и более простых, связанных между собой некоторыми логическими связями.
Формализация и преобразование связей между логическими переменными осуществляется в соответствии с правилами алгебры логики, называемой Буля (английский математик Джордж Буля).
Две логические переменные А и В, принимающие значение 0 или 1, могут образовать логические функции. Из 16 возможных функций двух переменных наибольший практический интерес представляют функции отрицания, логического умножения и логического сложения.
Логическое отрицание НЕ переменной А есть логическая функция X, которая истинна только тогда, когда ложно А, и наоборот.
В алгебре логики любые функции удобно изображать в виде таблицы соответствия всех возможных комбинаций входных логических переменных и выходной логической функции, называемой таблицей истинности. Для функции логического отрицания НЕ эта таблица имеет вид

 ,
,
где А – входная переменная, X – выходная функция.
Функцию НЕ в символах алгебры логики записывают следующим образом:
___
X=А
 |
Графически эта функция обозначается кружком на входе или выходе логического символа (рис. 4.1,а,б).
Рисунок 4.1 - Графическое изображение функции НЕ
Пример реализации функции НЕ представлены на рисунке 4.2

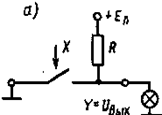
Рисунок 4.2 - Пример реализации логической функции НЕ (а) и ее временные диаграммы (б)
Примем положение переключателя за входную переменную и обозначим замкнутое состояние ключа логической единицей (X =1), а разомкнутое — логическим нулем (X = 0).
Логическое умножениеИ двух переменных А и В есть логическая функция X, которая истинна только тогда, когда одновременно истинны входные переменные. Для функции логического умножения таблица истинности имеет вид
| А | ||||
| В | ||||
| X |
В алгебре логики логическое умножение И иногда называют конъюнкцией и записывают в виде X = А • В или X = А ∩ В. Графически функция И обозначается в виде прямоугольника, внутри которого ставится символ & (рис. 4.3).

Рисунок 4.3 - Графическое изображение функции И
На рисунке 4.4 показан пример реализации логической функции X и диаграммы входных и выходных сигналов.
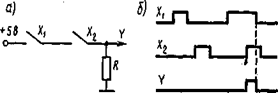
Рисунок 4.4 - Схема логической функции И (а), диаграмма входных
и выходных сигналов (б)
Логическая суммаИЛИ переменных А и В есть логическая функция X, которая истинна, когда хотя бы одна из входных функций истинна. Для логической суммы таблица истинности имеет вид
| А | ||||
| В | ||||
| X |
Логическая сумма в символах алгебры логики записывается .так:
X=A+B=AVB.
Пример реализации функции логической суммы двух переменных А, В и диаграммы входных и выходных сигналов представлены на рисунке 4.5.

а - графическое изображение;
б — схема логической суммы;
в - диаграммы входных и выходных сигналов
Рисунок 4.5 - Пример реализации логической суммы переменных А и В:
Три рассмотренных функции позволяют реализовать любую логическую зависимость.
 |  |
Рисунок 4.6 - Графическое изображение и временные диаграммы функции:
а -X = ИЛИ - НЕ; б -X = И - НЕ; в - X = =АВ+АВ
Широкое распространение получили в реализации современных логических схем функции ИЛИ—НЕ, И—НЕ, исключающие ИЛИ (рис. 4.6). Таблица истинности перечисленных функций соответственно имеет вид
| А | А | ||||||
| В | В | ||||||
| Х= ИЛИ -НЕ | Х=И-НЕ |
| А | ||||
| В | ||||
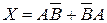
|
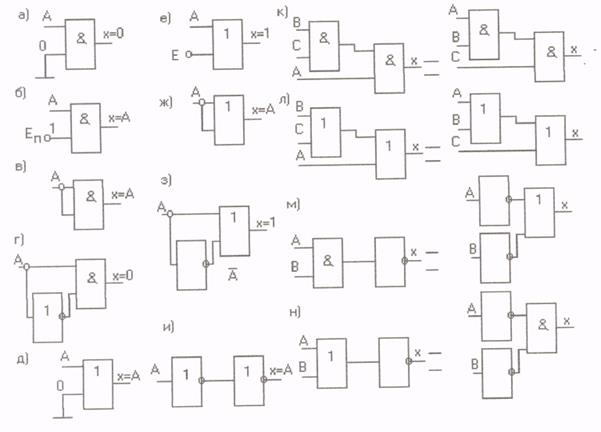
В таблице 1 приведен полный перечень функций двух аргументов. Функции, образованные логическими переменными, можно преобразовывать в соответствии с правилами или законами алгебры логики. При этом стремятся минимизировать логическое выражение, т.е. привести его к виду, удобному для практической реализации на логических элементах.
Таблица 1
| Функции | Аргументы | Обозначение функции | Название функции | ||||
| Х | |||||||
| Y | |||||||
| f 0(X,Y) | Константа 0 | ||||||
| f1 (Х,Y) | Х 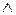 Y Y
| Конъюнкция (логическое И) | |||||
| f2 (Х,Y) | Х∆Y | Запрет по Y (отрицание импликации) | |||||
| f3 (Х,Y) | X | Переменная X | |||||
| f4 (Х,Y) | Y∆Х | Запрет по X (отрицание импликации) | |||||
| f5 (Х,Y) | Y | Переменная Y | |||||
| f6 (Х,Y) | X 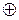 Y Y
| Сумма по модулю 2 | |||||
| f7 (Х,Y) | X 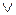 Y Y
| Дизъюнкция (логическое ИЛИ | |||||
| f8 (Х,Y) | X↓Y | Стрелка Пирса ( отрицание дизъюнкции) | |||||
| f9 (Х,Y) | X~Y | Эквивалентность | |||||
| f10 (Х,Y) | 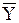
| Отрицание Y (функция НЕ) | |||||
| f11 (Х,Y) | Y→X | Импликация от Y к Х | |||||
| f12 (Х,Y) | 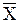
| Отрицание X (функция НЕ) | |||||
| f13 (Х,Y) | X→Y | Импликация от X к Y |
|
| f14 (Х, Y) | X\Y | Штрих Шеффера ( отрицание конъюнкции) | |||||
| f15 (Х,Y) | Константа 1 |
Рисунок 4.7 – Примеры преобразования логических функций: а- Х=А×0; б- Х=А×1=А; в- Х=А× 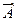 =А; г-Х= А×
=А; г-Х= А× 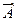 =0; д-Х=А+0=А; е-Х=А+1=1; ж-Х=А+А=А; з-Х=А+
=0; д-Х=А+0=А; е-Х=А+1=1; ж-Х=А+А=А; з-Х=А+ 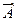 =1; и-Х=
=1; и-Х= 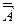 =А; к-Х=(А×В)×С=А×(В×С); л-Х=(А+В)+С=А+(В+С); м-
=А; к-Х=(А×В)×С=А×(В×С); л-Х=(А+В)+С=А+(В+С); м- 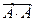 =
= 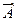 +
+ 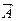 ; н-
; н- 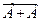 =
= 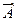 ×
× 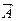
Рассмотрим наиболее распространенные правила алгебры .логики на примерах с минимальным количеством переменных (рис. 4.7).
Правило 1: X = А -0 = 0 (рис. 4.7,а). Логическое произведение любого аргумента на 0 всегда равно 0. Правило часто используется для выполнения процедуры "маскирования" входных переменных.
Правило 2: X =А • 1 = А (рис. 4.7,б). Логическое произведение любого аргумента на 1 равно значению аргумента.
Доказательства правил 1 и 2 можно получить подстановкой значений аргументов в таблицы истинности для логических функций И, ИЛИ.
Правило 3: X =А • А =А (рис. 4.7,в) . Логическое произведение одних и тех же аргументов равно аргументу. В таблице истинности этому правилу соответствуют значения аргументов
Правило 4: А • А =0. Логическое произведение аргумента с его инверсией равно 0.
Правила 5,6,1,8 касаются логической суммы и аналогичны рассмотренным правилам для логических произведений.
Правило 5:Х=А +0=А (рис. 4.7,д).
Правило 6: X =А + 1 = 1 (рис. 4.7,е).
Правило 7: Х = А+4 =А (рис. 4.7,ж).
Правило 8: X =А,+ А = 1 (рис. 4.7,з) .
Правило 9: X = А = А (рис. 4.7,и). Двойная инверсия аргумента дает его истинное значение.
Правило 10: X = А•В= В•А.
Правило 11:Х=А+В=В+А.
Правила 10 и 11 аналогичны переместительному закону алгебры и указывают на возможность перемещения аргументов в логических функциях И, ИЛИ.
Правило 12: АГ = (А-В) -С = А- (В-С) (рис. 4.7,к).
Правило 13: X = (А + В) + С = А + (В + С).
Правила 12 и 13 аналогичны сочетательному закону алгебры и показывают, что аргументы логических функций И, ИЛИ можно группировать произвольно.
Правило 14: X = А (В + С) = АВ + АС.
Правило 15:Х = А + (В-С) = (А+В)(А+С).
Правило 15 можно доказать при помощи составления и сравнения таблиц истинности для правой и левой частей каждой формулы, описывающей тот или иной закон:
Левая часть Правая часть
| А | 0 0 0 0 1 1 1 1 | А | 0 0 0 0 1 1 1 1 | ||
| В | 0 0 1 1 0 0 1 1 | В | 0 0 1 1 0 0 1 1 | ||
| С | 0 1 0 1 0 1 0 1 | С | 0 1 0 1 0 1 0 1 | ||
| В·С | 0 0 0 1 0 0 0 1 | А+В | 0 0 1 1 1 1 1 1 | ||
| А+С | 0 1 0 1 1 1 1 1 | ||||
| А+ВС, | 0 0 0 1 1 1 1 1 | (А+В)(А+С) | 0 0 0 1 1 1 1 1 |
Правило 16: X = А + АВ = А.
Правило 17: X = А + 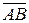 = А+ В.
= А+ В.
Правила 16, 17 применяют при преобразовании логических выражений.
Для доказательства правила 16 воспользуемся правилами 2 и 6:
А+АВ = А (1 + В)=А_•1=А, а_для доказательства правила 17 - правилом 15:
А+ 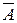 В=(А+
В=(А+  )(А+В)=(А+ В) =А +В.
)(А+В)=(А+ В) =А +В.
Правило 18: 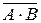 =
= 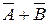 (рис. 4.7,м).
(рис. 4.7,м).
Правило 1.9: 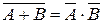 (рис. 4.7, н).
(рис. 4.7, н).
Правила 18, 19 известны как правила де Моргана, или законы инверсии.
Убедиться в справедливости правил 16—19 можно, если воспользуемся методом доказательства, который был применен для правила 15.
Правила алгебры логики применяют для преобразования исходных выражений к виду, удобному для их практической реализации. В этом случае логические функции задаются в виде таблицы истинности, в которой всем возможным значениям аргументов присваивается определенное значение функции. Например, в таблице 2 задана логическая функция Y трех переменных (А, В, С):
Таблица 2
| А | В | С | Y | А | В | С | Y | |
Эта функция принимает единичное значение при наборах переменных 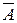 BC, AB
BC, AB 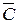 , ABC и в соответствии с этим может быть записана в виде уравнения
, ABC и в соответствии с этим может быть записана в виде уравнения
Y = 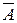 BC+АВ
BC+АВ 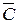 + ABC (1)
+ ABC (1)
Для реализации полученной логической функции потребуются три трехвходовые схемы И, одна трехвходовая схема ИЛИ и два инвертора. Правила алгебры логики позволяют преобразовать исходное уравнение к более удобному виду.
Во втором и третьем слагаемых уравнения (1) произведение АВ можно вынести за скобки:
Y= 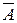 BС+ АВ(
BС+ АВ( 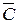 +C).
+C).
В соответствии с правилом 8 логическая сумма ( 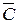 +С) = 1. Следовательно,
+С) = 1. Следовательно,
Y = 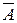 BC+АВ1 =
BC+АВ1 = 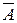 BC+ АВ.
BC+ АВ.
После вынесения за скобки общего множителя В имеем
Y = В( 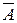 С+А).
С+А).
Применив для преобразования выражения в скобках правило 17, получим
Y = В( 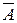 +А)(С+А) = В(С+А). (2)
+А)(С+А) = В(С+А). (2)
После раскрытия скобок уравнение (2) можно представить в виде
Y = ВС + АВ.
Очевидно, что уравнение (2) проще уравнения (1) для практической реализации и обеспечивает ту же выходную функцию (рис. 8).
Правила 18, 19 позволяют преобразовать уравнение (2) к виду, удобному для реализации схемы на других элементах

Рисунок 4.8 - Функциональная схема устройства

Рисунок 4.9 - Схема устройства в базисе элементов И-НЕ
Допустим, что для реализации схемы мы располагаем только элементами И— НЕ. Применим к (2) правила 9 и 19:
 Y =
Y = 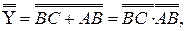 (3)
(3)
Схема, соответствующая уравнению (3) представлена на рисунке 4.9.
Для обеспечения минимизации логических уравнений можно использовать запись исходных данных в виде диаграмм Карно.
На рисунке 4.10, а, б представлены диаграммы Карно для трех переменных. Каждая клетка диаграммы соответствует логическому произведению прямого или инверсного значения переменных, присвоенных столбцу или строке, на пересечении которых она находится. Например, клетка с номером 0 находится на пересечении строки со значением переменной А и столбца со значениями переменных В и С соответствует логическому произведению ABC (рис. 4.10, а, б). В диаграммах Карно значения переменных присваиваются таким образом, чтобы соседние клетки по строкам и столбцам отличались между собой значением только одной переменной. Клетки, находящиеся на границах одной строки или одного столбца, считаются соседними.
На рисунке 4.11 представлена диаграмма Карно для четырех переменных и показаны значения логических произведений, соответствующие каждой клетке диаграммы.

а- с номером клетки, б — с логическим обозначением клетки
Рисунок 4.10 - Диаграммы Карно для трех переменных:

Рисунок 4.11 - Диаграмма Карно для четырех переменных
По описанию логической функции нескольких переменных на диаграммах Карно в клетки записывают значения логических произведений из таблицы истинности. На рисунке 4.12 представлена диаграмма Карно, соответствующая логической функции, заданной таблице 2

Рисунок 4.12 - Пример логической функции
Диаграммы Карно позволяют легко выделить произведения, которые можно упростить. Если произведения стоят в соседних клетках, то из общего выражения можно исключить одну переменную. Например, элементы 3 и 7 клеток (см. рис. 10, а) можно преобразовать к виду
ABC+ 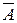 BC=(А+
BC=(А+ 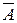 )•ВС=ВС.
)•ВС=ВС.
Элементы 6 и 7 клеток — соответственно к виду
AB 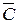 +ABC=АВ(
+ABC=АВ( 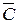 +С)=АВ.
+С)=АВ.
Одно и то же произведение можно использовать несколько раз в сочетании с другими. Применяя правило преобразования, функцию, представленную на рисунке 4.12, определяют уравнением
Y=АВ+ВС
а) 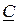
 б)
б) 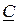 в)
в) 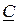 г)
г) 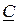
   
| А | А | А | ||||||||||||||||||
    1 1
| |||||||||||||||||||||
| В | В | В | |||||||||||||||||||



 D D D D
D D D D
F=AB F= 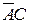 F=
F= 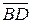 F=
F= 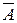
Рисунок 4.13 - Логические функции: а-F =АВ;б-F= 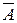 C;в-F—B
C;в-F—B 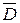 ;
;
г — F = 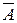
Используя правила 8, 14, 17, легко доказать, что четыре логических произведения, образующие столбец или строку, позволяют исключить из выражения аргументы, встречающиеся в прямом и инверсном кодах. Произведения, образующие квадрат (с учетом замкнутости краевых линий диаграммы), позволяют исключить из общего выражения две переменные. Основные варианты группирования клеток на диаграммах Карно представлены на рисунке 4.13, а – г.

Дата добавления: 2019-02-07; просмотров: 526;
