Интегральные уравнения
Интегральные уравнения позволяют получить более компактные выражения, а ГУ учитываются на этапе вывода ИУ.
Двумерный случай:
Металлический объект:
Е-поляризация, ИУ первого рода. Пусть имеется объект 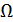 идеально проводящий,
идеально проводящий, 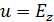 , выполняется условие излучения. На поверхности металла выполняется ГУ для полного поля:
, выполняется условие излучения. На поверхности металла выполняется ГУ для полного поля:
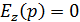 ,
, 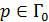
Считаем, что для полного поля отсутствует зависимость по 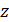 . Примером такой функции для возбуждающего первичного поля является нить электрического тока
. Примером такой функции для возбуждающего первичного поля является нить электрического тока 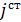 :
:
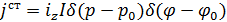
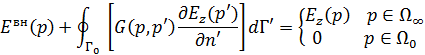
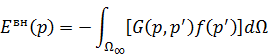
Учитывая 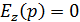 при
при 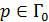 , получаем ИУ первого рода:
, получаем ИУ первого рода:
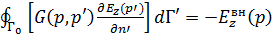 ,
, 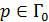
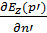 - магнитное поле.
- магнитное поле.
На поверхности металла магнитное поле испытывает скачок, пропорциональный поверхностному электрическому току.
Н-поляризация. ИУ второго рода. ГУ:
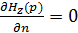 ,
, 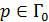
Первичное поле возбуждается нитью магнитного тока
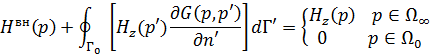
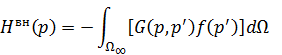
На контуре обращается в ноль производная полного поля.
Для гладких тел можно исключить особенность ядра из ИУ
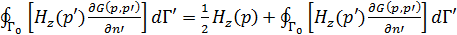 (в смысле главного значения)
(в смысле главного значения)
Интеграл с сильной особенностью заменяется интегралом в смысле главного значения. Особая точка 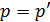 исключена из области интегрирования в виде выделенного свободного слагаемого.
исключена из области интегрирования в виде выделенного свободного слагаемого.
Получаем ИУ второго рода
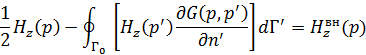
Дата добавления: 2019-02-07; просмотров: 384;
