Интегральные представления
Пусть имеется объект 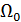 с границей
с границей 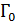 и внешней областью
и внешней областью 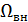 (граница
(граница 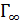 ) с расположенными в ней сторонними возбуждающими токами
) с расположенными в ней сторонними возбуждающими токами 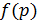 .
.
В области 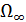 волновая функция
волновая функция 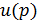 удовлетворяет уравнению Гельмгольца
удовлетворяет уравнению Гельмгольца
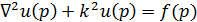 ,
, 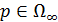 (1)
(1)
Волновая функция должна удовлетворять условиям излучения
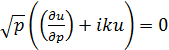 ,
, 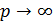
Необходимо получить интегральное представление функции 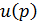 в области
в области 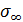 . Функция Грина удовлетворяет уравнениям Гельмгольца
. Функция Грина удовлетворяет уравнениям Гельмгольца
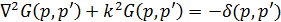 , (2)
, (2)
Для нахождения решения уравнения (1), умножим (1) на 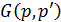 , а (2) – на ИУ. Выполняем вычитание левых и правых частей и интегрирование полученных выражений по области
, а (2) – на ИУ. Выполняем вычитание левых и правых частей и интегрирование полученных выражений по области 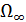 . В результате имеем:
. В результате имеем:
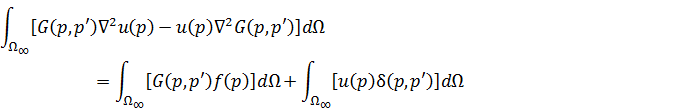
Далее выполняем следующие преобразования:
а). поверхностный интеграл заменим контурным при помощи скалярной теоремы Грина
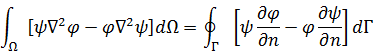
Функции, входящие в интеграл, непрерывны вместе с производными второго порядка везде, вплоть до контура 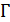 , который должен быть главкой по критерию Ляпунова (в каждой точке контура существует нормаль). Поскольку
, который должен быть главкой по критерию Ляпунова (в каждой точке контура существует нормаль). Поскольку 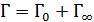 , а на
, а на 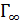 выполняется условие излучения, то в контурном интеграле остается интеграл по контуру
выполняется условие излучения, то в контурном интеграле остается интеграл по контуру 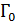 . Во втором слагаемом справа интеграл дает
. Во втором слагаемом справа интеграл дает 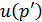 .
.
Из-за симметрии функции Грина (в функции Грина замена не делается) 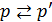 . В итоге получаем
. В итоге получаем
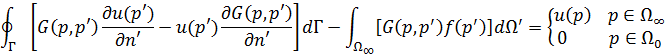
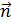 – внешняя нормаль по отношению к области
– внешняя нормаль по отношению к области 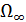 ,
, 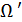 - область, где
- область, где 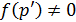 .
.
В результате, для нахождения решения в некоторой области 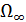 необходимо располагать сведениями о его поведении на границе
необходимо располагать сведениями о его поведении на границе 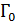 .
.
В контурный интервал входят 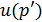 и
и 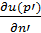 .
.
Если 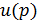 – электрическое поле, то
– электрическое поле, то 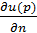 – магнитное поле. Если объект отсутствует, то
– магнитное поле. Если объект отсутствует, то
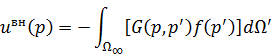
Дата добавления: 2019-02-07; просмотров: 444;
