Извлечение корня n-ой степени из комплексного числа.
Пусть дано комплексное число 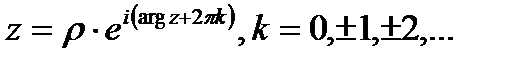 . Тогда
. Тогда 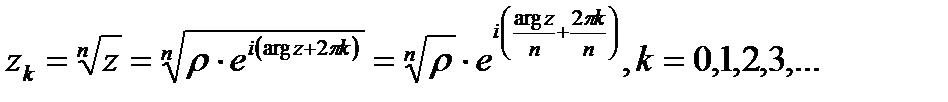 . (1.3)
. (1.3)
Отсюда видно, что при разных значениях 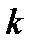 мы получаем разные комплексные числа, которые будут отличаться только своими аргументами. При этом количество таких комплексных чисел равно
мы получаем разные комплексные числа, которые будут отличаться только своими аргументами. При этом количество таких комплексных чисел равно 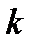 и они получаются при
и они получаются при 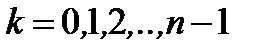 . При отрицательных значениях
. При отрицательных значениях 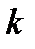 новые комплексные числа не получаются.
новые комплексные числа не получаются.
Если комплексные числа 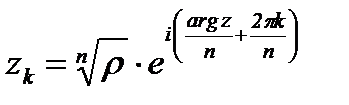
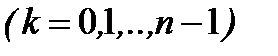 изобразить на комплексной плоскости, то они будут расположены в вершинах правильного n-угольника, радиус описанной окружности которого равен
изобразить на комплексной плоскости, то они будут расположены в вершинах правильного n-угольника, радиус описанной окружности которого равен 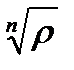 (рис. 1.12).
(рис. 1.12).
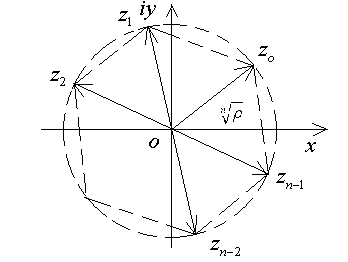
Рис. 1.12
Пример 1.3. Решить уравнение 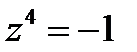 .
.
Решение.Согласно (1.3) имеем
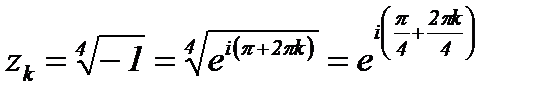 ,
, 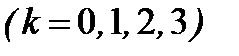 .
.
Отсюда c учетом формулы Эйлера 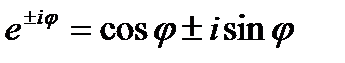 , имеем
, имеем
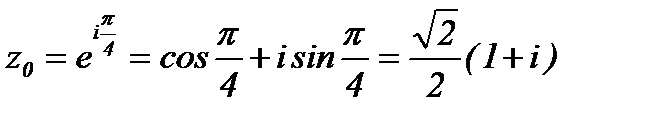 ,
, 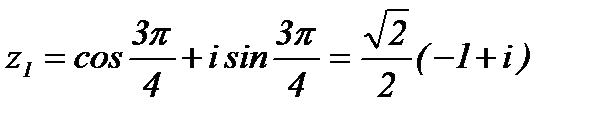 ,
,
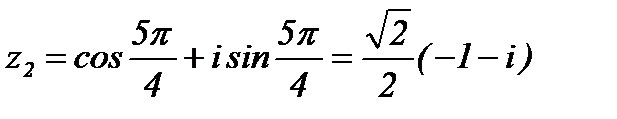
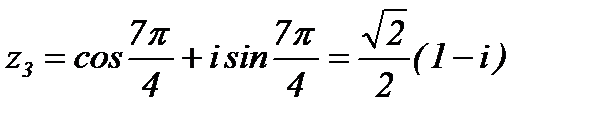 .
.
На рис. 1.13. приведено расположение решений исходного уравнения на комплексной плоскости.
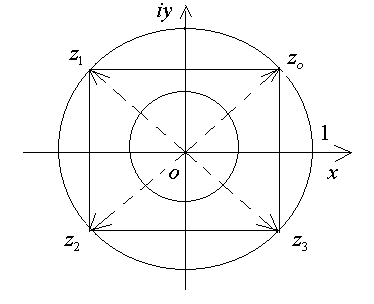
Рис. 1.13
Ответ: 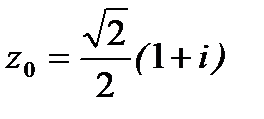 ;
; 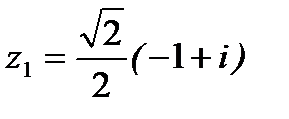 ;
; 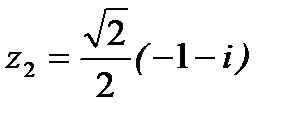 ;
; 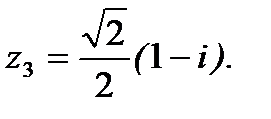
Пример 1.4.Найти 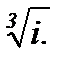
Решение.Согласно (1.3) имеем 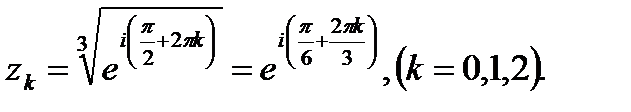 Отсюда с учетом формулы Эйлера, получим
Отсюда с учетом формулы Эйлера, получим
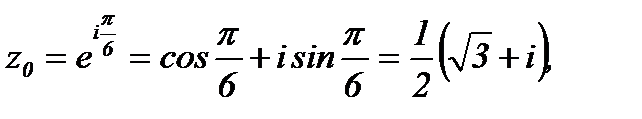
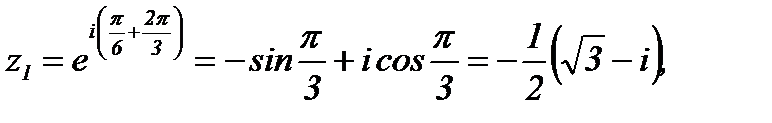
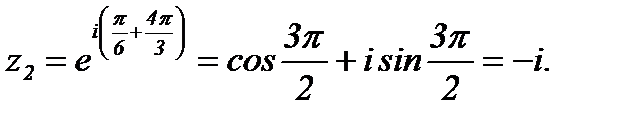
Ответ: 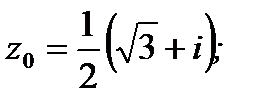
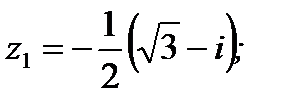
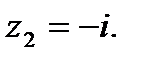
Задачи с ответами.
1.3.1. Найти 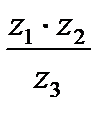 , если
, если 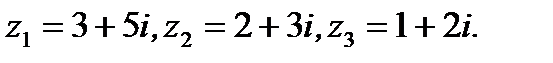
Ответ: 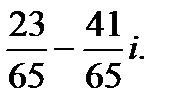
1.3.2. Найти 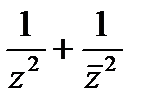 , если
, если 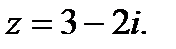
Ответ: 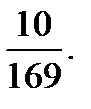
1.3.3. Упростить выражение 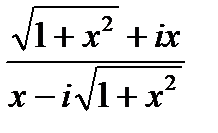 .
.
Ответ: 
1.3.4. Найти комплексные числа 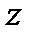 , которые удовлетворяют условиям
, которые удовлетворяют условиям
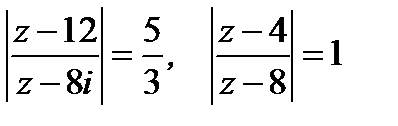 .
.
Ответ: 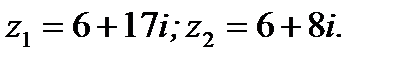
1.3.5. Вычислить 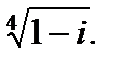
Ответ: 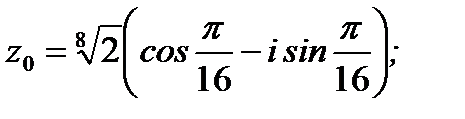
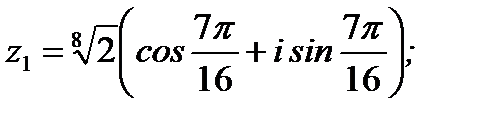
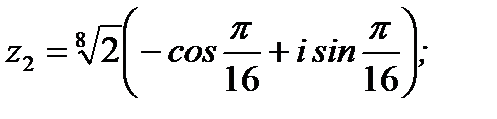
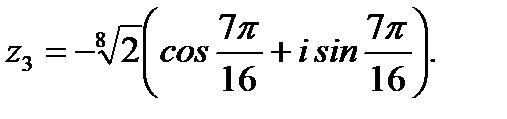
1.3.6. Вычислить 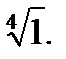
Ответ: 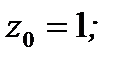
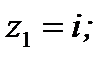
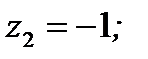
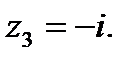
1.3.7. Вычислить 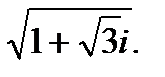
Ответ: 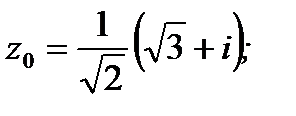
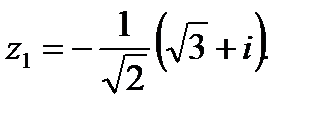
1.3.8. Решить уравнение 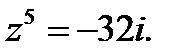
Ответ: 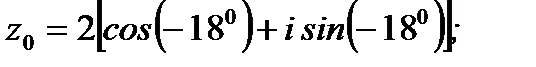
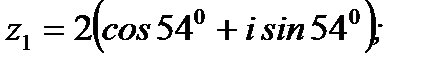
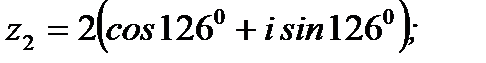
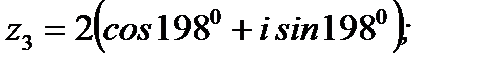
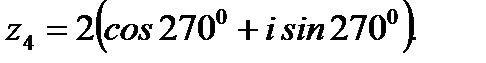
1.3.9. Решить уравнение 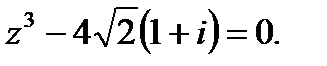
Ответ: 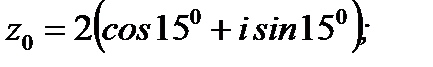
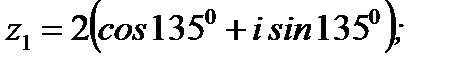
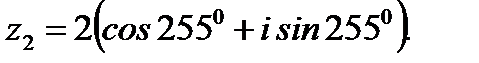
1.3.10. Решить уравнение 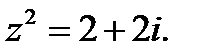
Ответ: 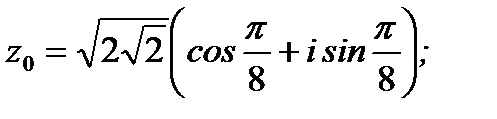
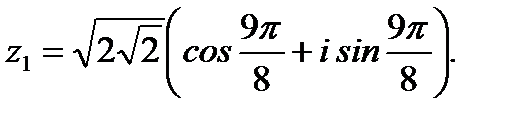
Дата добавления: 2018-11-25; просмотров: 782;
