Определение комплексного числа.

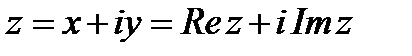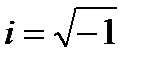Комплексным числом называется число , где - мнимая единица ( 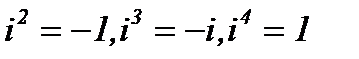и так далее), – действительные числа, 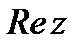- действительная часть комплексного числа, а 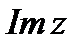- мнимая часть комплексного числа. Представление комплексного числа в виде 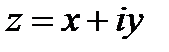называется алгебраической формой комплексного числа.

Геометрически комплексные числа изображают точками на комплексной плоскости . Кроме того, рассматривают 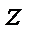как вектор, соединяющий начало координат на комплексной плоскости с точкой 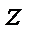(рис. 1.11).

Такая интерпретация комплексных чисел весьма удобна в ряде случаев. А кроме того все их свойства, которые мы перечислим ниже, укладываются в действия с векторами (сложение векторов, вычитание векторов, умножение вектор на число).

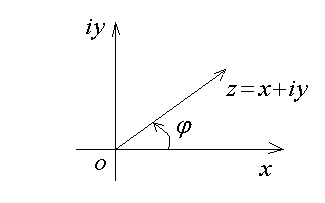
Рис. 1.11

Далее, если ввести угол 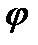между радиусом вектором и положительным направлением оси 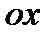и модуль комплексного числа как длина радиуса вектора ( 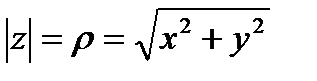), то число 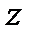можно записать в тригонометрической форме 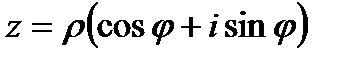. Если теперь учесть известную формулу Эйлера 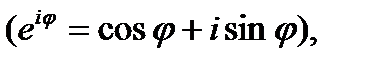то комплексное число 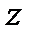можно представить в показательной форм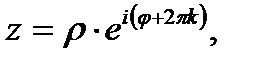е где 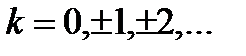Угол 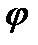называется главным значением 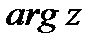и 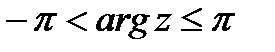. Итак имеем:

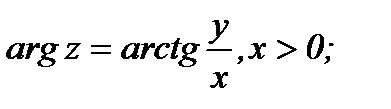
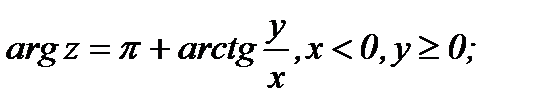(1.1)

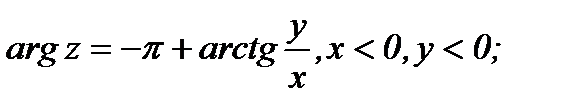
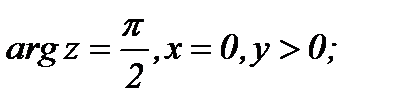
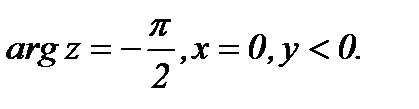(1.2)

Как видно из рисунка 1.11 каждое комплексное число имеет бесконечное количество аргументов. При этом справедливо соотношение .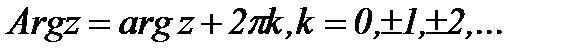

Заметим, что число 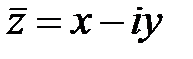называется сопряженным комплексным числом числа 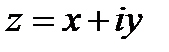и 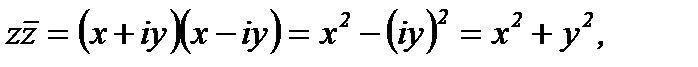то есть произведение комплексного числа на его сопряженное есть действительное число.