Определения элементарных функций и их свойства

Элементарные функции. Сведения о комплексных числах

Определения элементарных функций и их свойства

1. Степенная функция 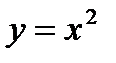обладает следующими свойствами:

1). Функция определена для всех действительных чисел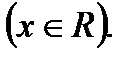

2). Функция четная, так как 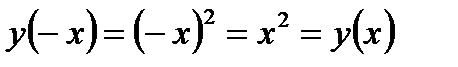(график симметричен относительно оси ординат).

3). При 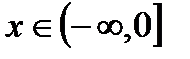функция убывает, а при 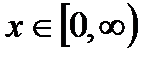функция возрастает.

4). При 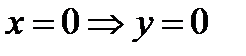(график функции проходит через начало координат).

5). 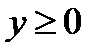для .

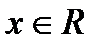6). Функция непериодическая.

График функции 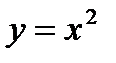называется параболой и приведен на рисунке 1.1.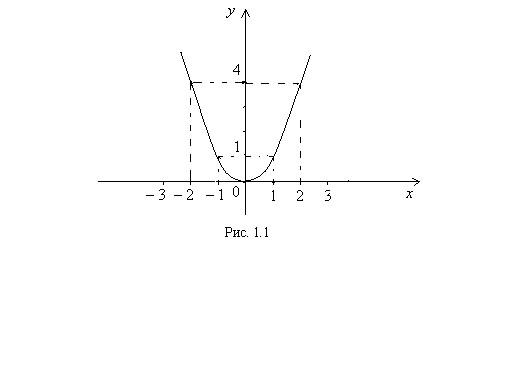

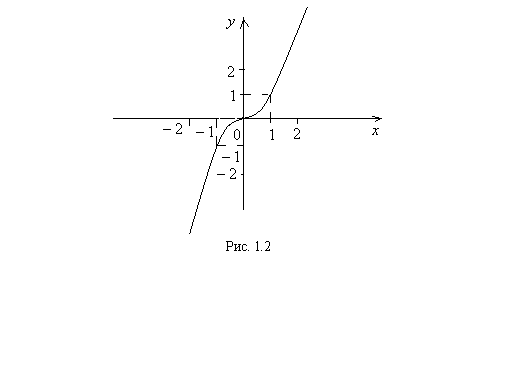
2. Степенная функция 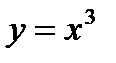обладает следующими свойствами:

1). Функция определена для всех действительных чисел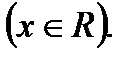

2). Функция нечетная, так как 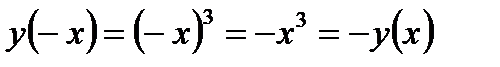(график симметричен относительно начало координат).

3). Функция возрастает для всех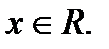

4). При 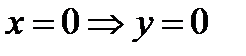(график функции проходит через начало координат).

5). Функция непериодическая.

График функции 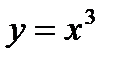называется кубической параболой и приведен на рисунке 1.2.

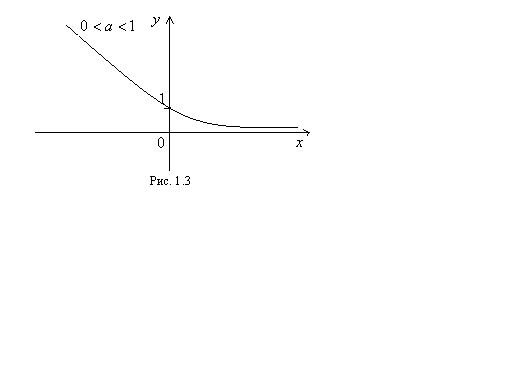
3. Показательная функция 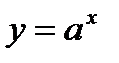при 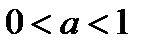обладает следующими свойствами:

1). Функция определена для всех действительных чисел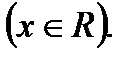

2). Функция не обладает четностью.

3). Функция убывает для всех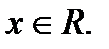

4). При 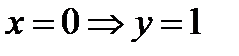(график функции проходит через точку с координатами (0;1)).

5). Функция непериодическая.

6). Функция принимает только положительные значения (график расположен выше оси ).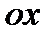

7).

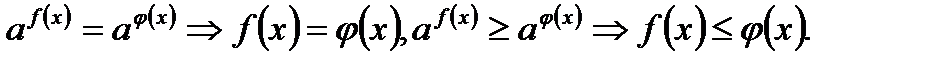
8).

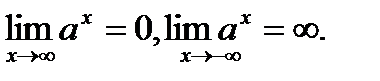
График функции приведен на рисунке 1.3.

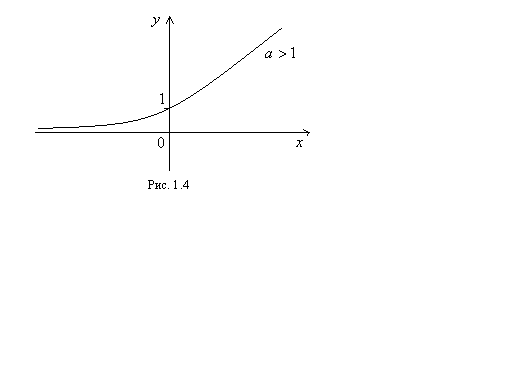
4. Показательная функция 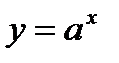при 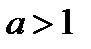обладает следующими свойствами:

1). Функция определена для всех действительных чисел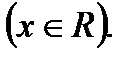

2). Функция не обладает четностью.

3). Функция возрастает для всех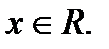

4). При 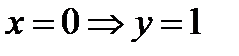(график функции проходит через точку с координатами (0;1)).

5). Функция непериодическая.

6). Функция принимает только положительные значения (график расположен выше оси ).

7).

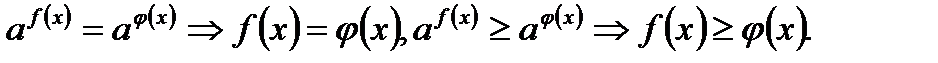
8).

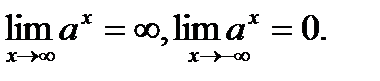
График функции приведен на рисунке 1.4.

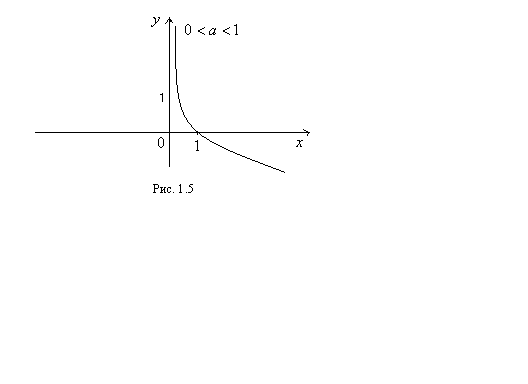
5. Логарифмическая функция 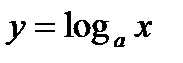при 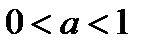обладает следующими свойствами:

1). Функция определена для всех действительных положительных чисел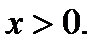

2). Функция не обладает четностью.

3). Функция убывает для всех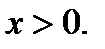

4). При 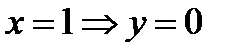(график функции проходит через точку с координатами (1;0)).

5). Функция непериодическая.

6). Функция является обратной показательной функции.

7).

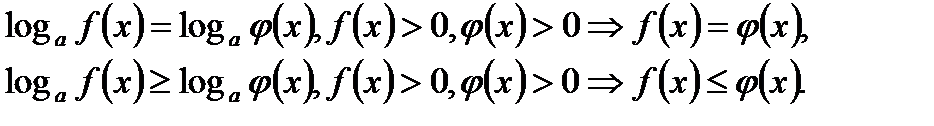
8).

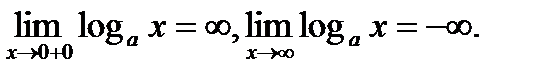
9). Функция имеет разрыв второго рода при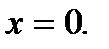

График функции приведен на рисунке 1.5.

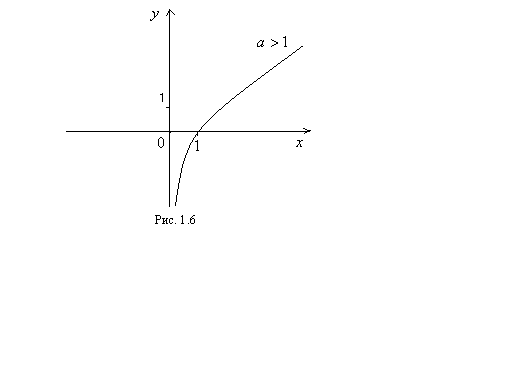
6. Логарифмическая функция 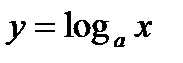при 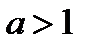обладает следующими свойствами:

1). Функция определена для всех действительных положительных чисел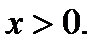

2). Функция не обладает четностью.

3). Функция возрастает для всех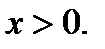

4). При 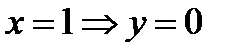(график функции проходит через точку с координатами (1;0)).

5). Функция непериодическая.

6). Функция является обратной показательной функции.

7).

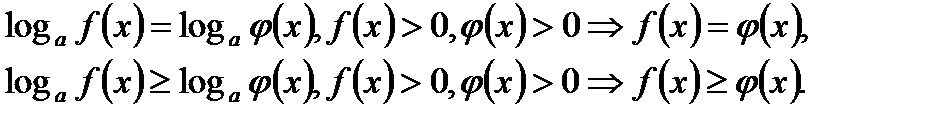
8).

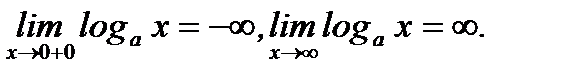
9). Функция имеет разрыв второго рода при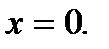

График функции приведен на рисунке 1.6.

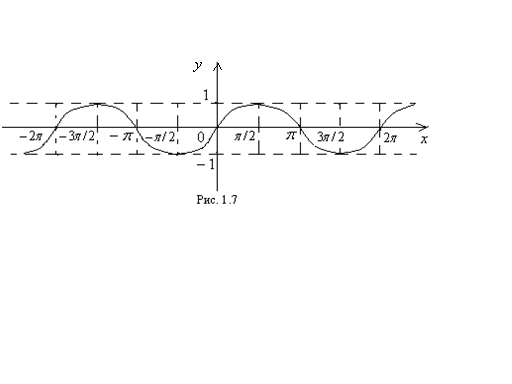
7. Свойства и график функции :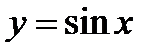

1). Функция определена для всех действительных чисел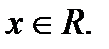

2). Функция нечетная, то есть 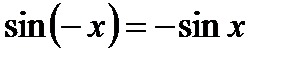(график симметричен относительно начала координат).

3). При 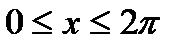функция возрастает на сегментах 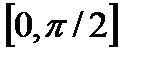и 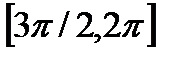, убывает на сегменте .

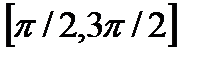4). Функция периодическая с наименьшим периодом 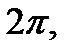то есть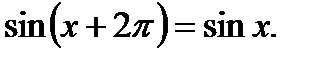

5). Множество значений функции – сегмент 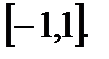Это означает, что 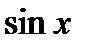удовлетворяет условию 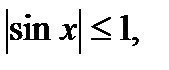то есть она ограниченная функция.

6). Функция непрерывная для всех значений аргумента из области определения.

График функции приведен на рисунке 1.7.

8. Свойства и график функции :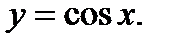

1). Функция определена для всех действительных чисел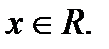

2). Функция четная, то есть 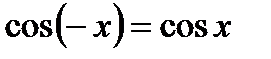(график симметричен относительно оси ординат).

4). При 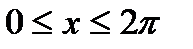функция убывает на сегменте 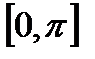, возрастает на сегменте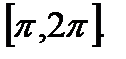

5). Функция периодическая с наименьшим периодом 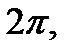то есть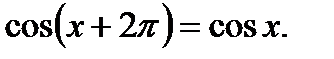

6). Множество значений функции – сегмент 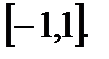Это означает, что 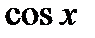удовлетворяет условию 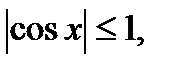то есть она ограниченная функция.

7). Функция непрерывная для всех значений аргумента из области определения.

График функции приведен на рисунке 1.8.

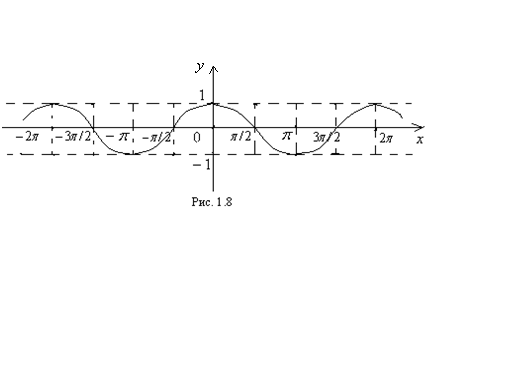
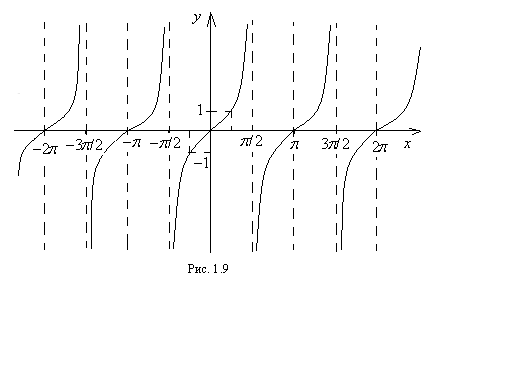
9. Свойства и график функции :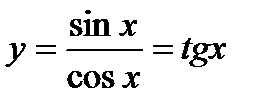

1). Область определения функции: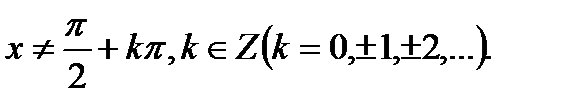

2). Функция нечетная, то есть 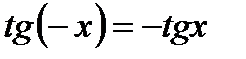(график симметричен относительно начала координат).

3). Функция возрастает на интервале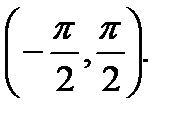

4). Функция периодическая с наименьшим периодом 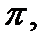то есть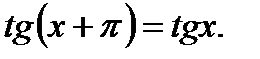

5). Множество значений функции – интервал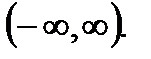

6). Функция имеет разрыв второго рода при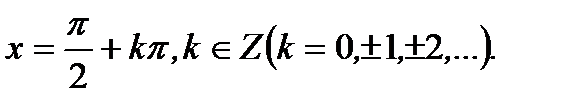

График функции приведен на рисунке 1.9.

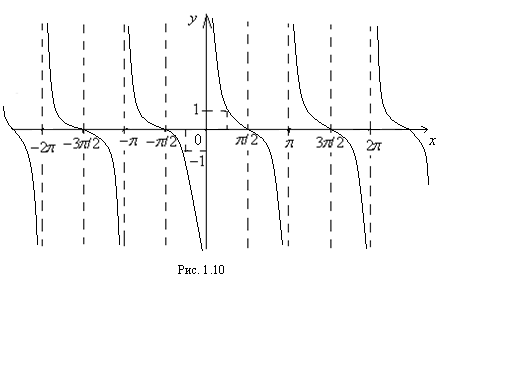
10. Свойства и график функции :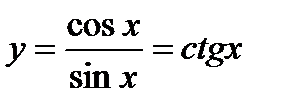

1). Область определения функции: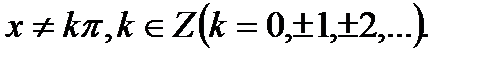

2). Функция нечетная, то есть 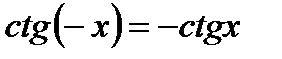(график симметричен относительно начала координат).

3). Функция убывает на интервале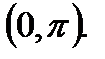

4). Функция периодическая с наименьшим периодом 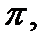то есть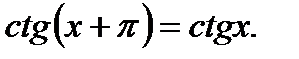

5). Множество значений функции – интервал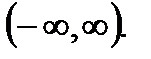

6). Функция имеет разрыв второго рода при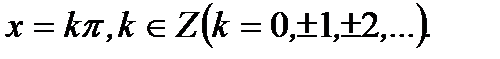

График функции приведен на рисунке 1.10.

Комплексные числа.