Диаграмма состояния двухкомпонентной системы

Если в воде растворить нелетучее вещество А (давление насыщенных паров вещества А много меньше давления насыщенных паров воды), которое не диссоциирует на ионы (a®0), то в двухфазном равновесии в растворе будут находиться молекулы вещества А и молекулы воды, а в газообразной фазе – только молекулы воды.

Давление насыщенного пара над жидкостью при данной температуре определяется равновесием между жидкой и газовой фазами. Это равновесие устанавливается на границе раздела фаз. Ему соответствует равенство скоростей испарения и конденсации.

В растворе концентрация молекул воды меньше, чем в чистой воде. Кроме того, молекулы воды участвуют в гидратации и часть их оказывается химически связанной с молекулами растворенного вещества. Это приводит к тому, что динамическое равновесие между раствором и газовой фазой устанавливается при меньшем давлении насыщенного пара растворителя. Очевидно, что увеличение концентрации нелетучего растворенного вещества приведет к уменьшению давления насыщенного пара растворителя при постоянной температуре.

Франсуа Рауль (Raoult) экспериментально установил, что при постоянной температуре относительное понижение давления насыщенного пара растворителя над разбавленным раствором равно мольной доле растворенного вещества X_А:

, ,

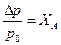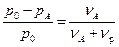где р₀и р_А – соответственно давление насыщенного пара чистого растворителя и растворителя над раствором; Dр = р₀ – р_А – понижение давления насыщенного пара растворителя; n_А и n_р – соответственно число молей растворенного вещества и растворителя. Это приведет к смещению положения линии равновесия жидкость↔газ (линия 1) в сторону меньших значений давления (линия 1¢) (рис.7.4).

Молекулы растворенного вещества затрудняют взаимную ориентацию молекул растворителя, соответствующую их положению в кристаллической решетке, т. е. препятствуют нормальному процессу кристаллизации воды. Это приводит к понижению температуры кристаллизации раствора по сравнению с чистым растворителем. На диаграмме это отражается смещением линии равновесия "твердая фаза ↔ жидкость" (линия 2) в сторону меньших температур (линия 2¢). Величина смещения будет пропорциональна концентрации растворенного вещества.

Эти изменения находятся в соответствии с правилом фаз Гиббса. В растворе число компонентов К=2. Следовательно, число степеней свободы для рассмотренных равновесий С = 2 + 2 – 2 = 2. В обоих случаях система будет бивариантной, т. е. можно изменять в определенных пределах одновременно два параметра без изменения числа фаз в системе. Например, давление насыщенного пара воды будет зависеть от температуры и концентрации растворенного вещества p=f(T,С_А). Температуры плавления и кипения растворов будут зависеть от давления и концентрации T=f(р,С_А).

В этом случае состояние равновесия двухкомпонентной системы будет определяться тремя независимыми параметрами: температурой, давлением и концентрацией растворенного вещества. Фазовая диаграмма раствора будет трехмерной. На плоскости ее построение возможно для конкретного раствора с концентрацией С (рис. 7.4).

Рассмотрим двухфазное равновесие "твердая фаза ↔ газ". При кристаллизации водного раствора обычно растворенное вещество выделяется в отдельную фазу. Число фаз в системе становится равным Ф=3. Поскольку число компонентов К=2, то число степеней свободы С = 2 + 2 – 3 = 1. Система в этом состоянии равновесия остается моновариантной. Давление насыщенного пара растворителя зависит только от температуры p=f(T). На диаграмме состояния линия 3 сохраняет свое положение (рис. 7.4).

Рис. 7‑4 Диаграммы состояния воды и водного раствора концентрации С (без строгого соблюдения масштаба)

В случае трехфазного равновесия «твердое состояние ↔ жидкость ↔ газ» число степеней свободы С = 2 + 2 – 3 = 1 (Ф=3, К=2). Система моновариантна, точка трехфазного равновесия будет находиться на линии 3. В отличие от однокомпонентной системы, ее координаты будут зависеть от концентрации растворенного вещества. Так, для раствора концентрации С это будет точка 0¢ (рис. 7.4).