Общая математическая модель формирования оптимальных решений
В математических моделях принятия решений в качестве нового знания выступает оптимальное решение, которое в наилучшем смысле соответствует достижению поставленной цели (целей).
Введем в рассмотрение n-мерный вектор X = (x1, x2, … , xn), определяющий количественные характеристики формируемого решения.
Обозначим через a, b, c вектора соответствующих размерностей, описывающие количественные характеристики неконтролируемых факторов.
Для оценки эффективности различных вариантов решений будем использовать специальным образом сформированную функцию:
W = f(c, X),
которая называется критерием оптимальности решений или целевой функцией задачи ПР.
Тогда выбор оптимального решения Хопт будем осуществлять, исходя из требования 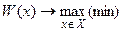 .
.
Множество Х должно быть допустимым с точки зрения учета условий принятия решений (ограничений).
Пусть ЛПР обладает для достижения цели вектором ресурсов b. Представим в виде вектор-функции j(а, Х) фактический расход ресурсов при использовании вектора решений Х и вектора некоторых факторов а.
Тогда j(а, Х) £ b есть ограничение.
Во многих задачах ПР учитывается условие Х ³0.
Таким образом, общая математическая модель формирования оптимальных решений может быть представлена в следующем виде:
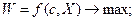 (4.1)
(4.1)
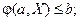 (4.2)
(4.2)
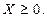 (4.3)
(4.3)
Постановка задачи в этом случае выглядит следующим образом:
Найти значение вектора Х, доставляющего максимум (минимум) критерию оптимальности решений (4.1) и удовлетворяющего при этом условиям (4.2) и (4.3).
Математическая модель ПР (4.1) – (4.3) является однокритериальной моделью.
Если ЛПР должен учитывать m целей, то, формализуя их в виде критериев оптимальности, получим:
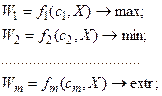 (4.4)
(4.4)
где c1 , c2 , …, cm – вектора неконтролируемых факторов.
Математическая модель (4.4), (4.2), (4.3) является многокритериальной моделью.
В реальных задачах ПР ограничения вида (4.2) могут включать в себя как неравенства вида «£», «³», «=», так и их различные сочетания.
4.3. Построение и решение оптимизационной
задачи принятия решения
(Задача о баке)
Пусть требуется выбрать геометрические размеры цилиндрического бака объемом V из условия минимального расхода материала на его изготовление.
Для построения математической модели введем в рассмотрение вектор проектных решений Х = (r, h), где 2r, h – диаметр и высота бака (Рис. 4.3).

 Если предположить, что бак изготавливается сваркой из трех деталей, то расход материала при произвольном векторе решений Х будет равен площади поверхности бака:
Если предположить, что бак изготавливается сваркой из трех деталей, то расход материала при произвольном векторе решений Х будет равен площади поверхности бака:
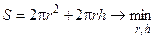 . (4.5)
. (4.5)
Согласно условиям задачи выражение (4.5) является целевой функцией (критерий оптимальности проектных решений).
Условие того, что бак должен иметь объем заданного значения V, представим в виде:
pr2h = V. (4.6)
На компоненты вектора решений X необходимо наложить дополнительные условия:
R > 0, h > 0. (4.7)
Выражения (4.5) – (4.7) описывают нелинейную однокритериальную модель формирования оптимальных решений, при n = 2, m = 1.
Пусть бак должен иметь минимальную трудоемкость его изготовления. Если считать трудоемкости изготовления крышки, дна и боковой стенки достаточно малыми величинами, то затраты времени на изготовление бака будут пропорциональны длине свариваемых швов:
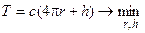 , (4.8)
, (4.8)
где с – затраты времени на сварку единицы длины.
Выражения (4.5), (4.8), (4.6), (4.7) описывают двухкритериальную нелинейную модель формирования оптимальных решений.
При построении математической модели в этой задаче принятия решений были использованы известные геометрические закономерности.
Аналитическое решение задачи ПР возможно, если соответствующая математическая модель включает в себя ограничения типа равенств, то есть имеет вид:
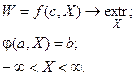
Такие задачи решаются обычно классическими методами условной оптимизации, которые предусматривают построение функции Лагранжа вида
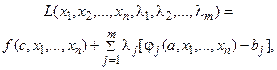 (4.9)
(4.9)
где l1, l2, … , lm – неопределенные множители Лагранжа.
Точки экстремума этой функции определяются из решения системы уравнений вида
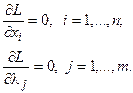 (4.10)
(4.10)
Решая эту систему, получим решение вида
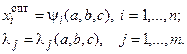 (4.11)
(4.11)
Используем этот метод для решения однокритериальной задачи (4.8), (4.6) (без учета (4.5), (4.7)).
Функция Лагранжа имеет вид:
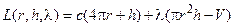 .
.
Система уравнений (4.17) относительно переменных r, h, l:
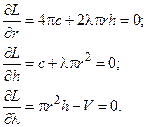
Имеем систему алгебраических уравнений, решая которую, получим значения неизвестных r, h (l находить необязательно):
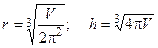 ;
; 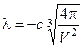 .
.
Таким образом, оптимальные размеры бака, найденные с помощью аналитического метода условной оптимизации, не зависят от затрат времени с на сварку единицы длины, но зависят от требуемого объема бака V. Требование (4.8) при этих значениях r и h выполняется, то есть трудоемкость будет минимальной.
Недостатками этого метода являются:
1) Не учитываются в явном виде условия неотрицательности (4.7).
2) Система уравнений (4.10) позволяет получить решение в форме (4.11) только для простых функций (4.5), (4.6).
Контрольные вопросы к лекции 11
1. Что включает в себя простейшая схема принятия решений?
2. Что такое цель?
3. Что такое критерий оптимальности?
4. Что такое однокритериальная ЗПР?
5. Что такое многокритериальная ЗПР?
6. Возможно ли получение единственного оптимального решения в многокритериальных задачах?
7. Напишите общий вид математической модели формирования оптимальных решений.
8. Сформулируйте задачу принятия решений.
9. Запишите критерий минимального расхода материала для задачи о баке.
10. Запишите критерий минимальной трудоемкости для задачи о баке.
11. Запишите общий вид функции Лагранжа.
12. Перечислите недостатки аналитического метода условной оптимизации.
4.4. Многокритериальные задачи принятия решений
Лекция 12
Во многих задачах принятия решений имеется несколько целей, которые хочет достичь ЛПР. Такие задачи сводятся к многокритериальным задачам вида:
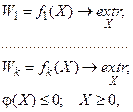
где Х (х1, х2,…хn) – вектор решений.
Наибольшее распространение на практике решения таких задач получил подход, связанный с работами итальянского математика-экономиста Викторио Парето. Он обеспечивает ЛПР возможность гибкого принятия решений. При оптимизации по Парето строится множество «неулучшаемых» решений, изменение каждого из которых ухудшает значение целевых функций f1(X), f2(X),…, fk(X).
Рассмотрим наиболее распространенную на практике двухкритериальную задачу оптимизации вида:
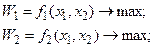 (4.12)
(4.12)
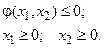 (4.13)
(4.13)
Условия (4.13) определяют множество допустимых решений и образуют на плоскости х1Ох2 некоторую область, каждой точке С которой соответствует точка С* в пространстве значений критериев W1OW2 (Рис. 4.4). Ее координаты 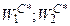 вычисляются по формулам (4.12) при х1 = х1С; х2 = х2С:
вычисляются по формулам (4.12) при х1 = х1С; х2 = х2С:
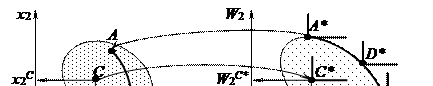 |
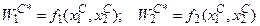 .
.
Рассмотрим в множестве значений критериев четыре точки A*, B*, D* и С*
(см. рис. 4.4). Точка А* является оптимальной для критерия W2 = f(x1,x2), так как в этой точке критерий W2 имеет максимальное значение. Аналогично точка В* является оптимальной для критерия W1 = f(x1, x2). Точка С* является «заведомо плохой» точкой, она не является оптимальной ни для одного критерия, так как в области значений критериев можно найти «более лучшую» точку D* такую, что 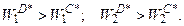 Для точек A*, B*, D* более «лучших» точек в пространстве значений критериев не существует. Такие точки составляют множество решений, оптимальных по Парето в пространстве значений критериев. В нашем случае это точки кривой A*D*B*. Для выделения «лучших» (неулучшаемых) точек используется понятие конуса Ki с вершиной в точке (
Для точек A*, B*, D* более «лучших» точек в пространстве значений критериев не существует. Такие точки составляют множество решений, оптимальных по Парето в пространстве значений критериев. В нашем случае это точки кривой A*D*B*. Для выделения «лучших» (неулучшаемых) точек используется понятие конуса Ki с вершиной в точке ( 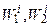 )
)
(Рис. 4.5). Уравнения этого конуса имеют вид: 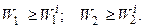
 Правило выделения «лучших» точек:
Правило выделения «лучших» точек:
Если в конусе Ki лежит хотя бы одна точка ( 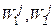 ), то она является более предпочтительной, чем точка (
), то она является более предпочтительной, чем точка ( 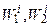 ) (см. рис. 4.5).
) (см. рис. 4.5).
Тогда все точки множества значений критериев, для которых соответствующие конусы являются пустыми, являются парето-оптимальными решениями в пространстве значений критериев.
Для нашего примера конусы, построенные во всех точках кривой A*D*B*
(см. рис. 4.4), являются пустыми. Строя обратное отображение этих точек в пространство решений Х, можно получить множество искомых решений (кривая АВ на рис 4.4), оптимальных по Парето. Такое множество называется множеством компромиссов, множеством эффективных точек или множеством Парето. Построив множество компромиссов, ЛПР выбирает в нем из неформальных соображений некоторую точку, которая является наилучшим компромиссом, по мнению ЛПР.
4.5. Построение решений, оптимальных по Парето
(Двухкритериальная задача о баке)
Вернемся к рассмотренной в п. 4.5 задаче о баке, описанную формулами (4.5) – (4.8), и попробуем найти паретооптимальное ее решение. Для этого введем параметры
a1 > 0 и a2 > 0, удовлетворяющие условию a1 + a2 = 1, и построим линейную свертку критериев (4.5) и (4.8):
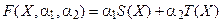 . (4.14)
. (4.14)
Положим a1 = 1, тогда a2 обращается в ноль, свертка (4.14) принимает вид
F(X) = S(X) и задача превращается в однокритериальную. Решив эту задачу, найдем оптимальную точку XS для обеспечения минимального расхода материала. Теперь положим
a1 = 0, тогда a2 = 1, свертка (4.14) примет вид F(X) = T(X). Решив эту однокритериальную задачу, найдем оптимальную точку XT, обеспечивающую минимальную трудоемкость изготовления бака. Если провести аналогию с рис. 7.4, то XS соответствует точке А, XT соответствует точке В. Чтобы определить промежуточные точки (остальные компромиссные решения), введем обозначение a = a1. Тогда a2 = 1 – a. Формула (4.14) примет вид 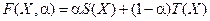 . Или:
. Или:
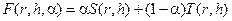 .
.
Функция Лагранжа запишется в виде
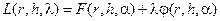 .
.
Распишем функцию Лагранжа подробнее:
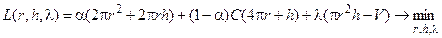 .
.
Чтобы найти минимум функции Лагранжа, нужно взять от нее производные по искомым переменным r, h, l и приравнять их к нулю.
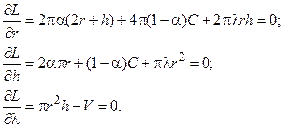 (4.15)
(4.15)
Получили систему трех алгебраических уравнений, решив которую найдем зависимость r, h, l от a. Задавая a от 0 до 1, получим множество решений, оптимальных по Парето. Поскольку аналитически решить систему (4.15) довольно сложно, можно воспользоваться любым численным методом, задавая предварительно значения a с любым приемлемым шагом.
 |
Для примера эта задача была решена с шагом 0,1 в пакете MathCad. На рис. 4.6 показано полученное множество паретооптимальных решений.
Рис. 4.6
ЛПР выбрал из этого множества точку при a = 0,4, при котором S = 2601; T = 802;
r = 10,44; h = 29,2. Эта точка устроила его потому, что при дальнейшем увеличении a
S уменьшается уже незначительно и Т имеет наименьшее значение из всех последующих.
Контрольные вопросы к лекции 12
1. Какие решения называются паретооптимальными?
2. Сформулируйте правило выделения лучших точек.
3. Что такое множество компромиссных решений?
4. Как получить множество компромиссных решений?
5. Запишите функцию Лагранжа для двухкритериальной задачи о баке.
6. Как найти минимум функции Лагранжа?
|
Сейчас, когда в стране происходит чуть ли не всеобщая компьютеризация, от специалистов различных профессий приходится слышать высказывания: "Вот внедрим у себя ЭВМ, тогда все задачи сразу же будут решены". Эта точка зрения совершенно не верна, сами по себе ЭВМ без математических моделей тех или иных процессов ничего сделать не смогут и о всеобщей компьютеризации можно лишь мечтать.
В подтверждение вышесказанного попытаемся обосновать необходимость моделирования, в том числе математического, раскроем его преимущества в познании и преобразовании человеком внешнего мира, выявим существующие недостатки и пойдем… к имитационному моделированию, т.е. моделированию с использованием ЭВМ. Но все по порядку.
Прежде всего, ответим на вопрос: что такое модель?
Модель – это материальный или мысленно представленный объект, который в процессе познания (изучения) замещает оригинал, сохраняя некоторые важные для данного исследования типичные свойства.
Хорошо построенная модель доступнее для исследования – нежели реальный объект. Например, недопустимы эксперименты с экономикой страны в познавательных целях, здесь без модели не обойтись.
Резюмируя сказанное можно ответить на вопрос: для чего нужны модели? Для того, чтобы
- понять, как устроен объект (его структура, свойства, законы развития, взаимодействия с окружающим миром).
- научиться управлять объектом (процессом) и определять наилучшие стратегии
- прогнозировать последствия воздействия на объект.
Что положительного в любой модели? Она позволяет получить новые знания об объекте, но, к сожалению, в той или иной степени не полна.
Модель сформулированная на языке математики с использованием математических методов называется математической моделью.
Исходным пунктом ее построения обычно является некоторая задача, например экономическая. Широко распространены, как дескриптивные, так и оптимизационные математические, характеризующие различные экономические процессы и явления, например:
- распределение ресурсов
- рациональный раскрой
- транспортные перевозки
- укрупнение предприятий
- сетевое планирование.
Каким образом происходит построение математической модели?
- Во–первых, формулируется цель и предмет исследования.
- Во–вторых, выделяются наиболее важные характеристики, соответствующие данной цели.
- В–третьих, словесно описываются взаимосвязи между элементами модели.
- Далее взаимосвязь формализуется.
- И производится расчет по математической модели и анализ полученного решения.
Используя данный алгоритм можно решить любую оптимизационную задачу, в том числе и многокритериальную, т.е. ту в которой преследуется не одна, а несколько целей, в том числе противоречивых.
Приведем пример. Теория массового обслуживания – проблема образования очередей. Нужно уравновесить два фактора – затраты на содержание обслуживающих устройств и затраты на пребывание в очереди. Построив формальное описание модели производят расчеты, используя аналитические и вычислительные методы. Если модель хороша, то ответы найденные с ее помощью адекватны моделирующей системе, если плоха, то подлежит улучшению и замене. Критерием адекватности служит практика.
Оптимизационные модели, в том числе многокритериальные, имеют общее свойство– известна цель(или несколько целей) для достижения которой часто приходится иметь дело со сложными системами, где речь идет не столько о решении оптимизационных задач, сколько об исследовании и прогнозировании состояний в зависимости от избираемых стратегий управления. И здесь мы сталкиваемся с трудностями реализации прежнего плана. Они состоят в следующем:
- сложная система содержит много связей между элементами
- реальная система подвергается влиянию случайных факторов, учет их аналитическим путем невозможен
- возможность сопоставления оригинала с моделью существует лишь в начале и после применения математического аппарата, т.к. промежуточные результаты могут не иметь аналогов в реальной системе.
В связи с перечисленными трудностями, возникающими при изучении сложных систем, практика потребовала более гибкий метод, и он появился – имитационное моделирование "Simujation modeling".
Обычно под имитационной моделью понимается комплекс программ для ЭВМ, описывающий функционирование отдельных блоков систем и правил взаимодействия между ними. Использование случайных величин делает необходимым многократное проведение экспериментов с имитационной системой (на ЭВМ) и последующий статистический анализ полученных результатов. Весьма распространенным примером использования имитационных моделей является решение задачи массового обслуживания методом МОНТЕ–КАРЛО.
Таким образом, работа с имитационной системой представляет собой эксперимент, осуществляемый на ЭВМ. В чем же заключаются преимущества?
–Большая близость к реальной системе, чем у математических моделей;
–Блочный принцип дает возможность верифицировать каждый блок до его включения в общую систему;
–Использование зависимостей более сложного характера, не описываемых простыми математическими соотношениями.
Перечисленные достоинства определяют недостатки
–построить имитационную модель дольше, труднее и дороже;
–для работы с имитационной системой необходимо наличие подходящей по классу ЭВМ;
–взаимодействие пользователя и имитационной модели (интерфейс) должно быть не слишком сложным, удобным и хорошо известным;
–построение имитационной модели требует более глубокого изучения реального процесса, нежели математическое моделирование.
Встает вопрос: может ли имитационное моделирование заменить методы оптимизации? Нет, но удобно дополняет их. Имитационная модель – это программа, реализующая некоторый алгоритм, для оптимизации управления которым прежде решается оптимизационная задача.
Итак, ни ЭВМ, ни математическая модель, ни алгоритм для ее исследования порознь не могут решить достаточно сложную задачу. Но вместе они представляют ту силу, которая позволяет познавать окружающий мир, управлять им в интересах человека.
Дата добавления: 2018-09-24; просмотров: 992;
