Тема 21. Объемные резонаторы

Свободные (собственные) колебания объёмных резонаторов. Общая теория свободных колебаний в резонаторах. Собственные параметры: резонансная частота, собственная (ненагруженная) добротность. Вынужденные колебания резонаторов, связанных с источником энергии и нагрузкой. Полная (нагруженная) добротность резонаторов. Объёмные резонаторы, образованные из отрезков линий передачи, короткозамкнутых или нагруженных на конце. Коаксиальные резонаторы. Прямоугольные и цилиндрические резонаторы.

Открытые резонаторы. Диэлектрические и ферритовые резонаторы.

Возбуждение волн в резонаторах.

Проходные резонаторы. Квазистационарные резонаторы.

Указания к теме

При рассмотрении объемных резонаторов следует обратить внимание на отличие полей в резонаторе и волноводе, обусловленное характером граничных условий. Необходимо знать собственные параметры резонатора и параметры нагруженного резонатора, эквивалентные схемы замещения ненагруженного и нагруженного резонаторов, связь элементов эквивалентных схем с параметрами резонатора. Важно уяснить физический смысл собственной, внешней и нагруженной добротностей резонатора и определение их через накопленную энергию и энергию потерь.

При изучении резонаторов из отрезков ЛП следует обратить внимание на условие резонанса в каждой из исследуемых разновидностей резонаторов, необходимо знать структуру поля на основном резонансе.

Основные сведения

В УВЧ диапазоне и выше применяют объемные резонаторы, ЭМ колебания которых возникают внутри ограниченного объема. На рис. 21.1 показано постепенное превращения LC-контура в объемный резонатор. К контуру из одного витка (рис. 21.1а), рассчитанному на ОВЧ, добавляем параллельно несколько витков (рис. 21.1б), что уменьшает излучение в пространство и повышает частоту контура. Объединение всех витков в сплошную поверхность приводит к тороидальному резонатору, ЭМП которого полностью локализовано в объеме резонатора (рис. 21.1в). Этот резонатор относится к классу квазистационарных, имеет четко выраженные области существования электрических и магнитных полей, его размеры малы по сравнению с l собственных колебаний.

Раздвинув пластины конденсатора (рис. 21.1б,в), получим сферическую поверхность. Собственная l такого резонатора станет сравнимой с его размерами. Весь объем резонатора (рис. 21.1г) будет в равной степени электрическим и магнитным полями, и в этом случае не удается выделить отдельные области со свойствами индуктивности и емкости.

ЭМ колебания могут существовать в ограниченном объеме любой формы, если размеры объема достаточно велики по сравнению с l. ЭМП в таком резонаторе можно представить в виде ЭМВ, вектор которой последовательно отражается от его стенок. Резонанс (резкое увеличение амплитуды колебаний) наблюдается в том случае, если эта ЭМВ приходит в определенную точку в одной и той же фазе.

Собственные колебания возникают в резонаторе при внешнем импульсном воздействии. Частота резонанса зависит от геометрических размеров резонатора и структуры ЭМП рассматриваемого типа волн. Объемные резонаторы имеют бесконечный ряд резонансных частот, соответствующих собственным колебаниям разного вида. (Путей для циркулирующего в резонаторе вектора ЭМВ, для которого выполняются условия резонанса, - бесконечное множество!)

Вынужденные колебания возникают в резонаторе при внешнем периодическом воздействии, при этом энергия в систему поступает каждый период. При совпадении частоты этого воздействия с одной из резонансных частот возникает резонанс.

Добротность резонатора определяется как отношение запасенной в резонаторе колебательной энергии к энергии потерь в резонаторе.

Отрезок полого металлического волновода прямоугольного сечения, на концах которого расположены металлические пластинки, образует прямоугольный параллелепипед со сторонами a, b и l по осям (рис. 21.2). Этот пример показывает, как из отрезков закрытых ЛП получаются закрытые объемные резонаторы.

Тогда формула для нахождения резонансной частоты имеет вид

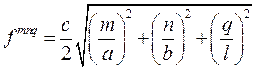, (21.1)

где кроме волноводных индексов m и n добавился индекс q, соответствующий числу полуволн по оси z.

Различные распределения ЭМП в резонаторе соответствуют модам типа Н_mnp и E_mnp, которые получаются сочетаниями индексов m, n и q.

Основной является мода Н₁₀₁ (при b < a и b < l). В многомодовом режиме в резонаторе существуют колебания нескольких типов. Устройства связи должны при этом обеспечивать избирательную по структуре поля связь резонатора с ЛП, подавляя колебания нежелательных типов.

Собственная добротность Q₀ равна умноженному на 2π отношению накопленной в резонаторе энергии к потерям энергии (в данном случае в проводнике резонатора) за период, и для моды Н_m0p определяется так:

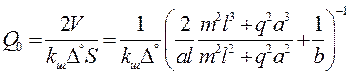, (21.2)

где V – объем, а S – площадь боковой поверхности объемного резонатора, k_ш – коэффициент шероховатости.

Объемные резонаторы применяются в диапазонах ОВЧ-ГВЧ в качестве резонансных систем в усилителях, генераторах, измерителях частоты (волномерах), для построения частотных фильтров. В генераторах с их помощью осуществляется отбор энергии от потока электронов, согласование нагрузки генератора с электронным прибором и стабилизация частоты. В устройствах обработки сигнала с их помощью реализуется селекция сигналов по частоте, они являются основными элементами конструкций переключателей типа «прием-передача». Объемные резонаторы являются основными элементами волномеров и анализаторов спектра.

На СВЧ и выше потери в проводниках резонаторов значительны, поэтому применяют открытые и диэлектрические резонаторы, которые обеспечивают более высокую добротность.

Список рекомендуемой литературы:[2, с. 255–287; 11, с. 318–342; 5, с. 162–197; 6, с. 289–317; 7, с. 213–243; 9, с. 308–341; 12, с. 277–302; 13, с. 311–354; 33, 48].