Тема 19. Волновые процессы в нерегулярных линиях

Факторы, определяющие нерегулярность линий передачи: конечность линии, наличие неоднородностей (нерегулярностей) на пути распространения волны. Суперпозиция распространяющихся падающей и отраженной волн.

Понятие о длинной линии. Процессы в линиях передачи (ЛП) конечной длины. Коэффициент отражения, коэффициент бегущей волны (КБВ), коэффициент стоячей волны (КСВ). Входное сопротивление нагруженной линии. Эквивалентное сопротивление линии в произвольном поперечном сечении. Трансформация сопротивлений. Влияние отражения от нагрузки на КПД ЛП.

Общие принципы согласования линий передачи с нагрузкой. Критерии согласования. Узкополосное согласование.

Указания к теме

Использование теории цепей с распределенными параметрами для описания СВЧ устройств справедливо лишь для устройств с Т-волнами, но в некоторых случаях применимо и для устройств с Е- и Н-волнами.

Необходимо четко знать определения КСВ, КБВ, коэффициентов отражения и передачи, пределы изменения этих параметров, а также способы их экспериментального измерения. С помощью круговой диаграммы Смита – Вольперта необходимо научиться решать типовые радиотехнические задачи, такие как определение коэффициента отражения и КСВ, определение входного сопротивления или проводимости отрезка ЛП.

Следует уяснить суть явления трансформации сопротивлений, изучить поведение входного сопротивления ЛП при различных видах нагрузок. Необходимо запомнить достоинства режима бегущей волны в ЛП. Этот режим обеспечивается применением согласующих устройств, выполненных чаще всего из отрезков ЛП и реактивных элементов.

Основные сведения

Основные понятия (КСВ, КБВ и т. д.) были введены в теме 9. Для ЛП с Z_с, нагруженной сопротивлением нагрузки Z_н, из (9.9) следуют формулы для коэффициента отражения и коэффициента прохождения :

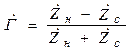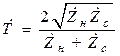; . (19.1)

Трансформация сопротивлений (проводимостей) в ЛП. Для получения зависимости сопротивления ЛП от продольной координаты нужно взять отношение волн U (17.9) к I (17.10), подставить в него коэффициенты отражения (9.9) и прохождения (9.4), что в результате дает:

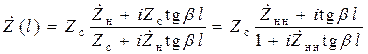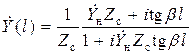; . (19.2)

Если линия согласована с нагрузкой, в линии распространяется только бегущая (прямая) волна, отношение волн U к I является постоянной величиной (Z(l) = Z_с), и трансформации сопротивлений не наблюдается.

В общем случае из-за трудностей расчета по (19.2) удобно использовать диаграммы полных сопротивлений (проводимостей), которые также часто называют диаграммами П. Х. Смита [2, 5, 33, 37, 49].

Для использования диаграммы сопротивлений при анализе согласования ЛП с нагрузкой необходимо нормировать Z_н относительно Z_c:

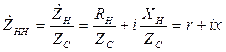. (19.3)

Линии постоянного активного нормированного сопротивления на диаграмме представляют собой окружности (рис. 19.1). На рис. 19.2 показаны линии постоянного реактивного нормированного сопротивления.

Положительные реактивности (индуктивного характера) откладываются в верхней части диаграммы (рис. 19.2), отрицательные реактивности (емкостного характера) – в нижней [37, 49].

Расстояние от точки пересечения линий активного и реактивного нормированного сопротивлений до центра окружности (r = 1, x = i0) определяет модуль коэффициента отражения. Практические конструкции диаграммы Смита обычно имеют закрепленную в центре прозрачную линейку с нанесенной шкалой модуля коэффициента отражения и КСВ.

При отсутствии такой линейки необходимо измерить расстояние до точки, соответствующей нормированному сопротивлению нагрузки, и максимальный радиус диаграммы. Отношение этих величин соответствует модулю коэффициента отражения [37, 49].

Очевидно, что линии постоянного КСВ или модуля коэффициента отражения на диаграмме представляют собой окружности, центры которых совпадают с центром диаграммы.

Фаза коэффициента отражения в градусах или относительных длинах (l/l определяется по прямой линии, проходящей из центра диаграммы через точку нормированного сопротивления нагрузки. Вокруг диаграммы за окружностью максимального радиуса нанесены шкалы для определения фазы коэффициента отражения. Максимальная фаза в относительных длинах волн равна 0,5 (период трансформации сопротивлений в ЛП равен l/2). При перемещении нагрузки вдоль ЛП от генератора или к генератору в ЛП без потерь модуль коэффициента отражения или КСВ не изменяются, а изменяется только фаза. Это расстояние в l/l прибавляется (или отнимается – в зависимости от направления сдвига) от фазы коэффициента отражения в длинах волн, что вызывает поворот от исходной точки. В новой точке значение комплексного сопротивления (или проводимости) нагрузки будет отличаться от исходного (трансформация сопротивлений!).

Хотя современная вычислительная техника позволяет производить необходимые расчеты без использования диаграмм Смита, из-за удобства и наглядности диаграммы Смита продолжают использоваться при инженерных расчетах (расчеты согласующих шлейфов, нерегулярностей в регулярных линиях передачи, режимов активных устройств и т. д.) [37, 49].

Идеально согласованной с нагрузкой считается ЛП при Г_н = 0 (Z_н = Z_с).

Генератор идеально согласован с ЛП при Z_г = Z_с (Г_г = 0).

Если ЛП не согласована с генератором, то отраженная от нагрузки ЭМВ отразится и от генератора, что приведет к появлению эхо-сигнала, который запаздывает относительно первичного на время τ = 2l/v_гр.

Если нет согласования с нагрузкой, то мощность ЭМВ, уносимая отраженной волной, не поступит в нагрузку, что снизит КПД системы.

КПД линии определяется как отношение мощности, поглощаемой нагрузкой, к мощности, приходящей от генератора на вход линии [2].

На практике не всегда удается выполнить оба критерия согласования, иногда оптимальный энергетический режим в системе «генератор – линия – нагрузка» достигается при несогласованных нагрузке и генераторе.

Особый интерес представляют случаи холостого хода (Zн ® ¥) и короткого замыкания (Zн = 0) ЛП. Из (19.2) следуют формулы для входных сопротивлений и проводимостей разомкнутого (19.4) и короткозамкнутого (19.5) шлейфов:

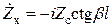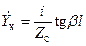, , (19.4)

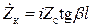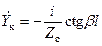, . (19.5)

На рис. 19.3 для обоих случаев показаны графики сопротивлений, из которых видно, что на отрезке ЛП длиной l/2 Z(l) принимает любые значения от –¥ до ¥.

Разомкнутый шлейф длиной от 0 до l/4 имеет чисто индуктивное сопротивление, а при длине от l/4 до l/2 – чисто емкостное сопротивление, при длине l/4 имеет место резонанс проводимости (подобно параллельному LС-контуру), а при длине от l/2 – резонанс сопротивления (подобно последовательному LС-кон­ту­ру).

Через каждые отрезки l/2 картина периодически повторяется.

Короткозамкнутый шлейф длиной от 0 до l/4 имеет емкостное, а при длине от l/4 до l/2 – индуктивное сопротивление, при длине l/4 имеет место резонанс сопротивления, а при длине от l/2 – резонанс проводимости.

Сопротивление некоторой точки l₀ численно равнопроводимости точки l₀ ± l/4. Этот эффект называют свойством четвертьволновой трансформации. Точка на диаграмме Смита, противоположная исходной (Z_нн) относительно центра (поворот на 180º или 0,25l), соответствует комплексной нормированной проводимости нагрузки (Y_нн=1/Z_нн).

Рассмотренные свойства сопротивления ЛП нашли применение в теории и практике направляющих систем и устройств СВЧ.

Реактивные шлейфы. Такой термин употребляется для отрезков ЛП с режимом короткого замыкания или холостого хода в сечении нагрузки.

Отрезки короткозамкнутых линий с длиной менее l/2 используют в качестве согласующих элементов, а также в качестве элементов колебательных контуров с распределенными параметрами.

С помощью шлейфа можно согласовать комплексную нагрузку с ЛП или генератором, изменяя длину шлейфа. Важным достоинством шлейфов является возможность их перестройки.

В согласующей схеме одиночный шлейф подключается параллельно основной ЛП на некотором расстоянии от нагрузки (Z_н ¹ Z_с). По сравнению с l/4-трансформатором в шлейфах можно использовать отрезок ЛП с таким же Z_с, как и в согласуемой ЛП. Согласование будет обеспечено, если шлейф подключить на таком расстоянии от нагрузки, где нормированная входная проводимость линии Y_нн = 1 ± iy. Проводимость шлейфа подбирается из условия компенсации реактивной составляющей ±iy проводимости Y_нн, что достигается подбором длины шлейфа [37, 49].

При проектировании согласующих схем обычно выбирают тот вариант, где шлейф короче, но окончательный выбор того или иного шлейфа может быть сделан лишь с учетом многих факторов, в частности их реализуемости. Например, в МПЛ исполнении более предпочтительна схема с разомкнутым шлейфом (при этом возможно паразитное излучение через выходное отверстие отрезка ЛП), а в коаксиальном – с замкнутым.

При изменении параметров нагрузки потребуется найти новое место подключения шлейфа в линию. Для устранения этого недостатка применяют систему из двух шлейфов. Один из шлейфов при изменении характеристик нагрузки будет подстраивать проводимость в области второго шлейфа до единичной активной составляющей (Y_нн = 1 ± iy), а второй шлейф скомпенсирует оставшуюся реактивность [37, 49].

Четвертьволновый трансформатор. Этот термин употребляется для отрезков линий с l = l/4. Это устройство позволяет согласовать ЛП с Z_с1 с нагрузкой или другой ЛП с Z_с2. Z_с устройства рассчитывают так :

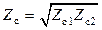. (19.6)

Физически работу согласующего l/4-трансформатора можно объяснить так: при оптимальных параметрах устройства волны, отраженные от первой и второй границ раздела, имеют одинаковые по модулю амплитуды и противоположные фазы (выбор длины согласующего перехода). Эта же идея положена в основу других узкополосных согласующих устройств (реактивные штыри, диафрагмы и т. п.) [37, 49].

Полное согласование обеспечивается только на определенной частоте, а также на кратных частотах, когда длина трансформатора составляет l/4 плюс целое число полуволн. При отклонении от расчетной частоты согласование ухудшается с ростом отклонения.

Рассмотренные устройства являются узкополосными. Для расширения полосы частот, в которой обеспечивается заданный КСВ в системе, устройства усложняют. Например, вместо l/4-трансформатора используют согласующий переход. Применяют как плавный, так и ступенчатый переходы. Появление большего числа границ раздела позволяет получить приемлемую компенсацию отраженных волн в широкой полосе частот.

Входное сопротивление неизвестной нагрузки, а также КСВ в линии, можно определить экспериментально с помощью измерительной линии. На измерительной линии при перемещении подвижного зонда связи с выхода детекторной секции снимают картину продольного распределения поля в линии и по отношению минимального и максимального значений напряжения находят КСВ (КБВ).

Список рекомендуемой литературы:[1, гл. 15, с. 69–70; 2, с. 174–186; 5, с. 212–222, 240–272; 11, с. 289–298, 310–318, 342–345;14; 18; 19; 27–29; 37, с. 29–30, 76–85; 49, с. 130–181].

Контрольные вопросы и задания

1. Дайте определение нерегулярностям в ЛП.

2. Опишите влияние нерегулярностей на распространение ЭМВ в ЛП?

3. Как определяется волновое сопротивление для волноводов?

4. Как определяют КПД линии передачи?

5. Опишите явление трансформации сопротивлений в линии передачи.

6. Опишите поведение сопротивления линии при ее коротком замыкании.

7. Опишите поведение сопротивления разомкнутой линии.

8. Дайте определение свойству четвертьволновой трансформации.

9. Приведите примеры эквивалентных емкостей и индуктивностей в линиях.

10. Дайте определение декомпозиции, матрицам рассеяния и передачи.

11. Как зависят коэффициенты отражения и передачи от длины линии?

12. Дайте определение и объясните особенности ЭМП стоячей ЭМВ.

13. Дайте определение и укажите область значений КСВ и КБВ.

14. Почему нежелательно появление стоячей ЭМВ в линии?

15. Опишите методику работы с диаграммой Смита – Вольперта.

16. Как на практике используют явление трансформации сопротивлений?

17. Назовите основные критерии согласования.

18. Дайте характеристику узкополосному и широкополосному согласованию.

19. Как отражения ЭМВ от нагрузки влияют на характеристики ЛП?