Нормальная составляющая на границе раздела сред претерпевает скачок, равный плотности поверхностного заряда.

При отсутствии поверхностного заряда (s_S = 0) нормальная составляющая вектора электрической индукции на границе раздела сред непрерывна, а нормальная составляющая вектора напряженности ( 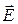) имеет разрыв, равный обратному отношению диэлектрических проницаемостей сред [1–4]:

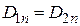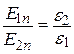; . (3.2)

Если обе среды обладают электропроводностью, то

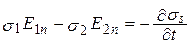. (3.3)

Для нормальныхсоставляющих векторовмагнитного поля [1–4]

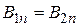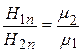; . (3.4)

Нормальная составляющая вектора магнитной индукции на границе раздела сред непрерывна, а нормальная составляющая 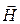имеет разрыв, равный обратному отношению магнитных проницаемостей сред.

Для тангенциальных (касательных)составляющих векторовэлектрического поля после преобразований [1–6] получаем

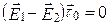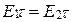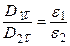, ; . (3.5)

Таким образом, тангенциальная составляющаявектора напряженности электрического поля на границе раздела сред непрерывна, а тангенциальная составляющаявектора электрической индукцииимеет разрыв, равный отношению диэлектрических проницаемостей сред.

Для тангенциальныхсоставляющих векторовмагнитного поля после преобразований [1–6] получаем :

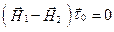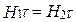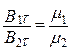, ; . (3.6)

Тангенциальная составляющая 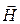на границе раздела сред непрерывна, а тангенциальная составляющая вектора магнитной индукцииимеет разрыв, равный отношению магнитных проницаемостей сред.

На границе идеального проводника (s®¥) возможно существование поверхностного тока проводимости (I_пов). (ЭМП высоких частот в металлическом проводнике концентрируется в тонком поверхностном слое, это явление рассматривается в теме 7.)

После преобразований [1–3] в результате получим

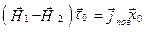. (3.7)

Таким образом, при наличии поверхностного тока тангенциальная составляющая вектора напряженности магнитного поля претерпевает скачок, равный плотности поверхностного тока.

Для векторов электрического и магнитного поля из векторных соотношений (см. рис. 3.1) и граничных условий (3.2)–(3.6) следует

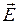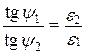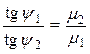() ; () . (3.8)

Из выражений (3.8) следует, что если параметры сред отличаются существенно (e₂ >> e₁ или m₂ >> m₁), то соответствующий вектор во второй среде будет направлен почти по нормали (на рис. 3.1 y₂ ® 90° ) независимо от угла наклона вектора в первой среде. Например, если e₂/e₁ = 100, то y₂ > 89° при y₁ >30°.

Список рекомендуемой литературы:[1, гл. 4, с. 21–23; 2, с. 39–43; 3, гл. 4, с. 22–24; 4, с. 21–23; 5, с. 13–15, 19–21; 6, с. 42–49; 7, с. 91–96; 8, с. 38–44; 9, с. 61–68; 10, с. 61–67; 11, с. 42–48; 12, с. 37–43; 13, с. 30–35].

Контрольные вопросы и задания

1. Для чего вводятся условия на границе раздела для векторов ЭМП?

2. Дайте формулировку граничных условий для нормальных составляющих векторов ЭМП.

3. Сформулируйте граничные условия для касательных составляющих векторов ЭМП.

4. При каких условиях вектор 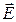во второй среде направлен практически по нормали при наклонной ориентации аналогичного вектора в первой среде?

5. Какая компонента ЭМП наводит поверхностный ток в проводящей среде?

6. Какие уравнения используются для вывода граничных условий?

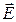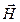7. Как зависит угол наклона векторов и во второй среде от расположения в первой среде и параметров сред?

8. Как влияет электропроводность сред на граничные условия?