Гидромеханика трубопроводов. Одномерное движение жидкости в трубе
Рассмотрим одномерное движение жидкости в трубе на участке 1-1 (рис. 9.1).
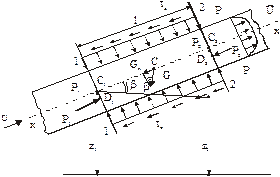
Рис. 9.1. Движение жидкости на участке трубы
При равномерном движении эпюры скоростей 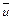 одинаковы в поперечных сечениях по длине трубы.
одинаковы в поперечных сечениях по длине трубы.
Составим уравнение равновесия суммы проекций внешних сил на ось движения Х, действующих на отсек 1 – 2, в виде 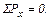

Силы давления приложены в центрах давления 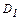 и
и 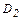 и равны
и равны 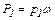 и
и 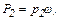 где
где 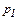 и
и 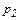 - давления в центрах тяжести сечений
- давления в центрах тяжести сечений 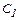 и
и 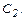
По смоченной боковой поверхности потока 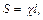 где
где 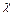 - смоченный периметр, а l – длина отсека, действуют давления
- смоченный периметр, а l – длина отсека, действуют давления 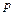 , направленные по нормали, и касательные напряжения
, направленные по нормали, и касательные напряжения 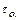
По всей смоченной поверхности действуют силы трения 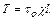
Силы тяжести жидкости 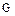 в отсеке 1 – 2 в проекции на ось
в отсеке 1 – 2 в проекции на ось 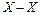 равны
равны
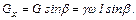 (9.1)
(9.1)
Из треугольника 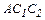 и силового треугольника с гипотенузой
и силового треугольника с гипотенузой 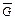 найдем
найдем
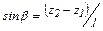 (9.2)
(9.2)
и
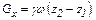 (9.3)
(9.3)
Проекции всех сил дают уравнение
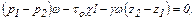 (9.4)
(9.4)
что после перегруппировки и деления на 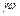 позволяет записать
позволяет записать
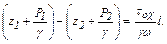 (9.5)
(9.5)
Поскольку скоростной напор в равномерном движении постоянен, то есть 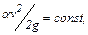 то потери напора равны
то потери напора равны
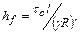 (9.6)
(9.6)
где 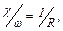 а
а 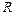 - гидравлический радиус.
- гидравлический радиус.
Величина 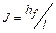 - гидравлический уклон, поэтому основное уравнение равномерного движения будет
- гидравлический уклон, поэтому основное уравнение равномерного движения будет
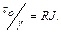 (9.7)
(9.7)
Величина касательных напряжений в большинстве задач квадратично зависит от скорости
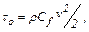 (9.8)
(9.8)
где 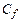 - коэффициент местного трения.
- коэффициент местного трения.
Из предыдущего уравнения следует
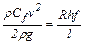 (9.9)
(9.9)
или
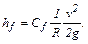 (9.10)
(9.10)
Учитывая, что 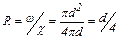 , и обозначив
, и обозначив 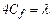 получим формулу Дарси-Вейсбаха для потерь по длине
получим формулу Дарси-Вейсбаха для потерь по длине
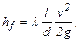 (9.11)
(9.11)
где 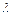 - коэффициент трения или коэффициент Дарси.
- коэффициент трения или коэффициент Дарси.
Обозначив 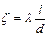 , получим формулу
, получим формулу
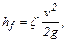 (9.12)
(9.12)
которая называется формулой Вейсбаха.
Это обобщение формулы Дарси-Вейсбаха дает возможность рассчитывать местные сопротивления.
Из формулы 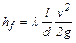 с учетом
с учетом 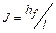 и
и 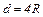 получим формулу Шези
получим формулу Шези
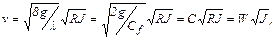 (9.13)
(9.13)
где 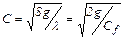 - коэффициент Шези с размерностью в СИ
- коэффициент Шези с размерностью в СИ 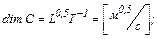
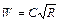 - модуль скорости с размерностью
- модуль скорости с размерностью 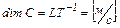
Дата добавления: 2018-06-28; просмотров: 772;
