Режимы движения жидкости. Число Рейнольдса

Механизм перемещения отдельных частиц изучался О. Рейнольдсом путем их визуализации. Струйка жидкости подкрашивалась и ее характер фиксировался при разных средних скоростях (рис. 9.2).

В результате установлено, что до некоторой скорости 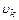график функции 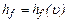является прямой и потери энергии линейно возрастают с возрастанием скорости. Затем функция 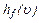становится квадратичной 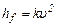. Области разделяются критической скоростью .

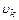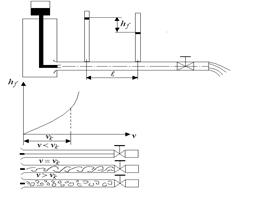
Рис. 9.2. Опыты Рейнольдса

В области до критической скорости режим движения ламинарный (слоистый). Затем появляются поперечные пульсации и движение становится вихревым. Наконец, с ростом скорости процесс становится хаотическим и режим становится турбулентным.

Обобщение условий смены режима движения определяется безразмерным параметром, называемым числом Рейнольдса:

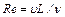, (9.14)

где 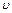- скорость потока; L- характерный размер; 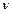- кинематическая вязкость.

Критические точки перехода от одного режима движения к другому характеризуются нижним и верхним числами Рейнольдса

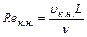и 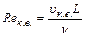, (9.15)

причем

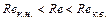(9.16)

Формула Пуазейля

При ламинарном режиме движения касательное напряжение в круглой трубе при равномерном движении имеет вид

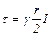, (9.17)

где 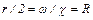- гидравлический радиус.

Распределение давлений в трубе подчиняется гидростатическому закону.

Касательные напряжения по закону Ньютона равны

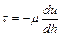, (9.18)

поэтому с учетом предыдущего и интегрирования

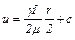. (9.19)

из условия нулевой скорости на стенках трубы 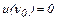получим

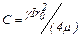, (9.20)

поэтому

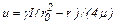. (9.21)

Эпюра скоростей в живом сечении будет параболоидом вращения и максимум достигается на оси трубы

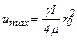. (9.22)

Элементарный расход в кольцевом сечении равен

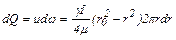. (9.23)

Интегрирование в пределах от r=0 до r=r₀ дает

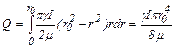. (9.24)

Средняя скорость потока равна

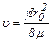. (9.25)

Потери напора определяются из условия 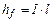, поэтому

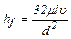. (9.26)

Это формула Пуазейля.