Экспоненциальное сглаживание временных рядов

К методам механического выравнивания временных рядов относится и метод экспоненциального сглаживания. Особенность данного метода заключается в том, что в процедуре нахождения сглаженного уровня используются значения только предшествующих уровней ряда, взятые с определённым весом. В данном случае вес наблюдения уменьшается по мере удаления его от момента времени, для которого определяется сглаженное значение уровня ряда. Сглаженные значения находятся по формуле:

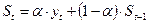(4.4),

где α – параметр сглаживания, а (1 – α) – коэффициент дисконтирования.

Используя данное соотношение для всех уровней ряда, начиная с первого и заканчивая моментом времени t, можно получить, что экспоненциальная средняя, т.е. сглаженное данным методом значение ряда динамики, является взвешенной средней величиной всех предшествующих уровней, т.е.

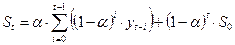(4.5),

где S₀ – величина, характеризующая начальные условия.

В практических задачах обработки экономических временных рядов рекомендуется (необоснованно) выбирать величину параметра сглаживания в интервале от 0,1 до 0,3. Других точных рекомендаций для выбора оптимальной величины параметра α пока нет.

Что касается начального параметра S₀, то в различных задачах его величина может быть равной:

1) первому значению ряда;

2) средней арифметической нескольких первых членов ряда;

3) среднему значению ряда, если имеем дело со стационарным процессом.

Указанная очерёдность выбора величины S₀ обеспечивает хорошее согласование сглаженного и исходного рядов для первых наблюдений. Если при подходе к последним наблюдениям ряда динамики сглаженные данным методом значения начинают значительно отличаться от соответствующих значений исходного ряда, то необходимо использовать другой параметр сглаживания, т.е. величину α.

Важным преимуществом данного метода является то, что ни одно значение исходного ряда не теряется, т.е. все сглаженные значения получены в соответствии с выбранной математической моделью.