Константы упругости

Количественно упругость характеризуется константами, свойственными каждому материалу. При этом необходимо учитывать, что большинство свойств, кроме плотности и теплоемкости, связано с анизотропией структуры. Упругость является ярко выраженным анизотропным свойством. Поэтому следует различать упругость кристаллов и анизотпропных материалов и упругость изотропных тел.

Поликристаллические тела и материалы в целом изотропны, анизотропия их свойств проявляется только в результате формования или обработки, например прессования, штампования, прокатки, уплотнения и т.п. Таким образом, формируется анизотропия свойств керамической плитки, черепицы, стального листа и т.д. В дальнейшем рассматривается упругость только изотропных свойств, для которых не применимы представления об ориентированных кристаллографических осях и пр.

С учетом вышеизложенного для большинства природных и искусственных материалов (горные породы, керамика, бетон, металлы и т.д.) при малых деформациях зависимости между напряжениями «σ» и деформациями «ε» можно считать линейными (рис. 5.2) и описывать обобщенным законом Гука:

σ = Еε,

где Е — модуль упругости (модуль Юнга).

Подобным образом напряжение сдвига «τ» прямо пропорционально относительной деформации сдвига или углу сдвига у(рис. 5.3):

τ = G . у

где G — модуль сдвига.

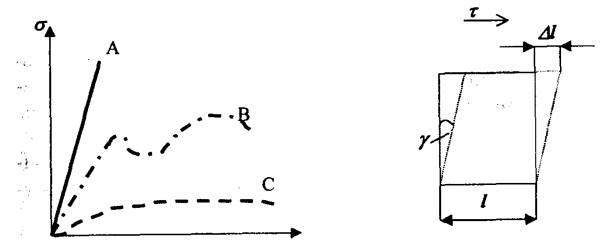
Рис. 5.2. Классическая зависимость напряжение — деформация:

А — керамики; В — металлов; С — полимеров

Рис. 5.3. Упругая деформация твердого тела при сдвиге

Удлинение образца при растяжении сопровождается уменьшением его толщины (рис. 5.4). Относительное изменение толщины Δl/l к относительному изменению длины Δd/d называется коэффициентом Пуассона «μ» или коэффициентом поперечного сжатия:

μ = (Δl/l) / (Δd/d).

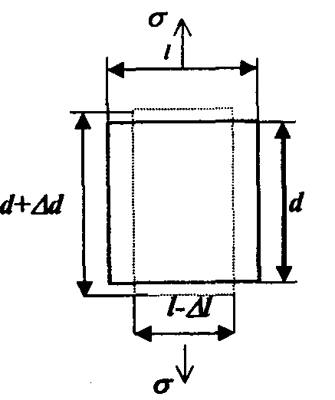
Рис. 5.4. Упругая деформация твердого тела при растяжении

Если при деформации тела его объем не изменяется, а это может иметь место только при пластическом или вязком течении, то μ = 0,5. Однако, практически, эта величина значительно ниже теоретического показателя и для разных материалов она различна. Упругие материалы (бетон, керамика и др.) имеют невысокие значения коэффициента Пуассона (0,15-0,25), пластичные (полимерные материалы) — более высокие (0,3-0,4). Это объясняется зависимостью между силами притяжения и отталкивания и изменением межатомного расстояния при деформации.

Модуль Юнга

Модуль Юнга, или модуль продольной деформации Е показывает критическое напряжение, которое может иметь структура материала при максимальной ее деформации до разрушения; имеет размерность напряжений (МПа).

Е =σ_р/ε;

Где: σ_р – критическое напряжение.

У поликристаллических материалов обычно наблюдаются отклонение от линейной σ = ƒ(ε,), несвязанное с энергией кристаллической решетки, а зависящей от структуры материала. Для оценки упругих свойств таких материалов применяют два модуля упругости: касательный Е = tgα и секущий V= tgβ, который называют модулем деформаций (рис. 5.5).

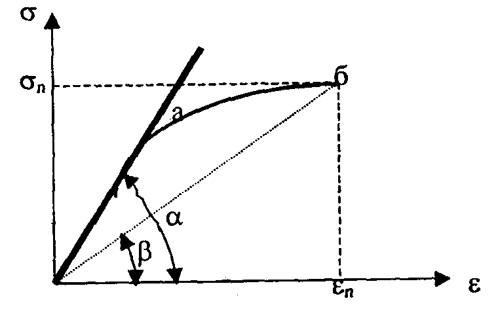
Рис. 5.5. Схематическое изображение деформации огнеупоров:

а — кривая деформации; б — точка разрушения;

σ; — предельное напряжение при разрушении; ε — деформация

Величина модуля упругости двухфазной системы является средней между величинами модулей упругости каждой из фаз, и аналитическое выражения для ее нахождения аналогичны тем, что используются при различных значениях линейного КТР:

Е = Е₁V₁ + E₂V₂,

где V₁ и V₂ — относительные объемные доли первой и второй фаз.

Это соотношение используется при разработке стеклопластиков, т.е. пластмасс, армированных стекловолокном. Е стекловолокна (~7^.10⁴ МПа) велик по сравнению с Е пластмасс (Е = 0,7^.10⁴ МПа). Поэтому даже при низкой объемной доле стекловолокна в композиции на него как на более прочный компонент приходится большая часть общей нагрузки.